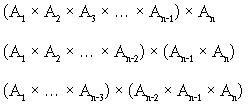Matrix Chain Multiplication & Linear Programming - part I
Matrix Chain Multiplication
โจทย์ของการคูณเมตริกซ์คือ ต้องการคูณเมตริซ์ n ตัว ยิ่ง n มากการจัดการคูณยิ่งลำบาก
เมื่อ m คือขนาดของเมตริกซ์
ถ้า Anm × Bmp ความเร็วในการคูณเมตริกซ์ A B = O (n×m×p)
1.ดังนั้นการจัดลำดับของการคูณจะมีผลต่อความเร็ว โดยการจัดลำดับนั้น ก็คือการจัดกลุ่มของการคูณ (Associative)
2.รูปแบบการคูณครั้งสุดท้ายมีได้ n-1 แบบ
ในการจัดกลุ่มของการคุณ ต้องดูกรณีที่เป็นไปได้ว่ามีกี่กรณีที่สามารถนำเมตริซ์มาคูณกันได้
พิจารณา เมื่อเริ่มแบ่งกลุ่มจะได้ว่า
จากนั้นคูณหาผลลัพธ์เพื่อดูว่าการจัดกลุ่มแบบไหนจัดการได้ง่ายสุด
สมมุติให้มีการคูณกันของ 5 เมตริกซ์
เราสามารถแบ่งแยกออกเป็นปัญหาย่อยได้
เมื่อเราแบ่งกลุ่มการคูณออกไปเรื่อยๆ จะสังเกตุว่าเกิดรูปแบบการคูณขึ้นซ้ำ ซึ่งหากเราวิเคราะห์และจัดการกับกรณีที่เกิดซ้ำๆได้ จะมีผลในเรื่องของความเร็ว หมายความว่าจำนวนครั้งในการคูณก็จะลดลง
ดังนั้นวิธีการที่จะนิยามปัญหานั้นเริ่มด้วย
1.แตกปัญหาใหญ่ออกมาเป็นปัญหาย่อยๆ
2.แปลงปัญหาย่อยให้อยู่ในรูป abstract
เรานิยามปัญหานี้ว่า
กำหนดให้ Xij แทนจำนวนครั้งของการคูณที่น้อยที่ใดในการคำนวณ 
m : คือจำนวนครั้ง
ตัวอย่าง
A1 × A2 × A3 × A4 × A5 ให้หา X15 กำหนดค่า row/column ของแต่ละเมตริกซ์เป็น
(10×100) × (100×20) × (20×400) × (400×200) × (200×100) ตามลำดับ
วิธีที่ง่ายคือตีตาราง
เมื่อ i=j คือการคูณตัวเองผลลัพธ์เป็นศูนย์
สังเกตุว่า 
หรือ 
ค่าจะเท่ากัน ในการคิดเราสามารถคิดตัวใดตัวหนึ่งแทนได้
จากตารางจึงคิดแค่ส่วนเดียวคือส่วนที่ไม่ระบายสี เทคนิคที่ช่วยจำกรณีเกิดการซ้ำของการคูณในการทำ recursion คือ Memorization
Linear Programming
แบบจำลองทางคณิตศาสตร์วิเคราะห์ปัญหาการวางแผน(planning)
การผลิตและการจัดการภายใต้ข้อจำกัด (Subject to) ของปัจจัยการผลิตชนิดต่างๆ เพื่อเลือกทางเลือกที่มีความเหมาะสมมากที่สุด
(อันได้แก่ กำไรสูงสุดหรือต้นทุนต่ำสุด)
ทบทวน
สมการเชิงเส้น คือ ความสัมพันธ์ของตัวแปร 
เช่น
ตัวอย่าง
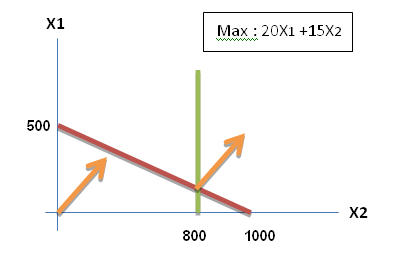
โรงงานรับผลิตรองเท้าข้างซ้ายและข้างขวา ให้
จำนวนรองเท้าของซ้าย
จำนวนรองเท้าข้างขวา
S.B. 
ต้องผลิตจำนวนรองเท้าข้างซ้ายเท่ากับข้างขวา
จำนวนเพชรที่ใช้ในการผลิต คือ ข้างซ้าย 2 เม็ต ข้างขวา 1 เม็ด โดยมีจำนวนเพชรทั้งหมด1000 เม็ด
Linear Programming: Max Flow
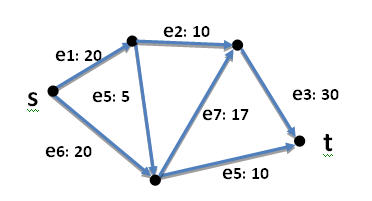
f1, ….,f7 โดย f1, ….f7 ≥ 0
Objective : max f1+f6
f1 ≤ 20, f2 ≤ 10, f6 ≤ 20
f6 = f2+f4 , f6+f4 = f7+f5
Linear Programiming : Max Flow Node V = { 1,2…..,n } , source S, Sink
Capacity C : VxV -> R
ตัวแบ่ง : V u,v f(u,v) แทน flow จากโนด u ไป v
Subject to ∀ u,v f (u,v) = - f (v,u)
∀ u,v f (u,v) ≤ C (u,v)
∀ u,v ไม่เป็นสมาชิก {s,t}
Shortest Paths by Linear Programming
ให้กราฟ G = (V,E) , Source S, Destination t, ความยาว l : E-> R
Maximize D(t)
เงื่อนไข
