ผลต่างระหว่างรุ่นของ "204512-53/lecture13"
G521455033 (คุย | มีส่วนร่วม) |
G521455030 (คุย | มีส่วนร่วม) |
||
| (ไม่แสดง 26 รุ่นระหว่างกลางโดยผู้ใช้ 3 คน) | |||
| แถว 1: | แถว 1: | ||
จดบันทึกคำบรรยายโดย: | จดบันทึกคำบรรยายโดย: | ||
| − | นายเสกสิทธิ์ สุวรรณ รหัสนักศึกษา 5214550332 | + | นายเสกสิทธิ์ สุวรรณ รหัสนักศึกษา 5214550332 <br> |
| + | นางสาวสลิตตา นกขุนทอง รหัสนักศึกษา 5214550308 | ||
== '''NP Complete''' == | == '''NP Complete''' == | ||
| + | [[ไฟล์:Npcomg521455.jpg]] <br> | ||
'''ปัญหา''' A <math>\leqslant</math> P (Polynomail time to) ปัญหา B ถ้า มี poly-time algo ที่สำหรับทุกๆ instance x ของ A <br> | '''ปัญหา''' A <math>\leqslant</math> P (Polynomail time to) ปัญหา B ถ้า มี poly-time algo ที่สำหรับทุกๆ instance x ของ A <br> | ||
x' = T(x) , | x' | = poly (| x |) <br> | x' = T(x) , | x' | = poly (| x |) <br> | ||
| แถว 10: | แถว 12: | ||
THM: 3-SAT <math>\leqslant</math> p INDEP-SET | THM: 3-SAT <math>\leqslant</math> p INDEP-SET | ||
Proof: ให้ <math>\varnothing</math> เป็น 3-CNF ใดๆ <br> | Proof: ให้ <math>\varnothing</math> เป็น 3-CNF ใดๆ <br> | ||
| − | |||
และ m clause เรียกเป็น <math>C_1,C_2,C_2,...,C_M</math> จะสร้างกราฟได้ดังนี้ | และ m clause เรียกเป็น <math>C_1,C_2,C_2,...,C_M</math> จะสร้างกราฟได้ดังนี้ | ||
**ในแต่ละ clause <math>C_i</math> สร้างสามเหลี่ยมที่ประกอบไปด้วยโหนดตัวแปรที่ปรากฎใน C ได้กราฟที่มี 3 โหนด ตามรูป | **ในแต่ละ clause <math>C_i</math> สร้างสามเหลี่ยมที่ประกอบไปด้วยโหนดตัวแปรที่ปรากฎใน C ได้กราฟที่มี 3 โหนด ตามรูป | ||
| แถว 19: | แถว 20: | ||
ที่ทำให้ทุก clause เป็นจริงพร้อมกัน <br> | ที่ทำให้ทุก clause เป็นจริงพร้อมกัน <br> | ||
เนื่องจาก Ci เป็นจริงจะมีตัวแบ่งอย่างน้อย 1 ตัวใน Ci เป็นจริง,เลือกโหนดใน G ที่สอดคล้องกับตัวแปรตัวนั้นใส่ Set I โดยที่ Set I ที่มีสมาชิก M ตัว <br> | เนื่องจาก Ci เป็นจริงจะมีตัวแบ่งอย่างน้อย 1 ตัวใน Ci เป็นจริง,เลือกโหนดใน G ที่สอดคล้องกับตัวแปรตัวนั้นใส่ Set I โดยที่ Set I ที่มีสมาชิก M ตัว <br> | ||
| + | จะพิสูจน์ว่า I เป็น Independent set ใน G <br> | ||
| + | assume ว่า I ไม่เป็น independent Set นั้นคือเชื่อมระหว่างบางคู่ของโหนด u,v <math>\epsilon</math> I <br> | ||
| + | เนื่องจากเชต I มีโหนดเพียงโหนดเดียวจากแต่ละสามเหลี่ยมดังนั้นไม่มีทางที่เส้นเชื่อมดังกล่าวจะเป็นเส้นเชื่อมในสามเหลี่ยมได้ | ||
| + | ดังนั้น ต้องเป็นเส้นเชื่อมระหว่างตัวแปร Xi บางตัวกับ <math> \lnot x_i \Rightarrow </math> เนื่องจากเราเลือกตัวแปรจาก assign ที่เป็นจริง กรณีที่ป็นไปไม่ได้ | ||
| + | นั้นคือ I เป็น Independent set ในกราฟมีขนาด m <br> | ||
| + | x1 = T , x2 = T ,x3 = F , x4 = T <br> | ||
| + | Ex สมมุติมี formular <br> | ||
| + | <math>( \lnot x_4 \or x_1 \or \lnot x_3 ) \and (x_1 \or x_2 \or x_3) \and ( \lnot x_3 \or \lnot x_1 \or x_4)</math> <br> วาดกราฟได้ดังรูป<br>[[ไฟล์:Npcomplete5214550332.jpg]] <br> | ||
| + | พิสูจน์ x1= T, x2=T , x3 = F ,x4 = T ให้เป็นจริง | ||
| + | <br>สูจน์ให้ได้ว่า clause 1.เป็นจริง <br>2.เป็นจริง <br>3.เป็นจริง <br> | ||
2.ถ้า G มี independent Set ขนาด m แล้ว <math>\varnothing</math> Satisfiable | 2.ถ้า G มี independent Set ขนาด m แล้ว <math>\varnothing</math> Satisfiable | ||
| + | |||
| + | ---- | ||
| + | '''SUBSET SUM''' | ||
| + | ในเซต A = {x1,x2,x3,..,xn} จำนวนเต็ม | ||
| + | มี subset B \subseteq A ที่ <math>= \sum_{x e 0} x = t </math> <br> | ||
| + | '''ต้องการพิสูจน์ว่า''' <br> | ||
| + | '''thm:''' 3-SAT <math>\leqslant</math> subset-sum <br> | ||
| + | '''Ex.''' <math>(\lnot \or x_4 \or x_2 \or \lnot x_3 ) \and (x_1 \or \lnot \ x_2 \or x_3) \and (\lnot \ x_3 \or \lnot \ x_1 \or x_4)</math> <br> | ||
| + | '''จะได้ว่า''' | ||
| + | |||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | ! | ||
| + | ! | ||
| + | ! C | ||
| + | |||
| + | |- | ||
| + | |x1 | ||
| + | | 1 0 0 0 0 | ||
| + | | 1 | ||
| + | |- | ||
| + | |<math>\lnot</math>x1 | ||
| + | | 1 0 0 0 0 | ||
| + | | 0 | ||
| + | |||
| + | |- | ||
| + | |x2 | ||
| + | |0 1 0 0 0 | ||
| + | | 0 | ||
| + | |||
| + | |- | ||
| + | |<math>\lnot</math>x2 | ||
| + | | 0 1 0 0 0 | ||
| + | | 1 | ||
| + | |||
| + | |- | ||
| + | | x3 | ||
| + | | 0 0 1 0 0 | ||
| + | | 1 | ||
| + | |||
| + | |- | ||
| + | |<math>\lnot</math>x3 | ||
| + | | 0 0 1 0 0 | ||
| + | | 0 | ||
| + | |- | ||
| + | | | ||
| + | | 1 1 1 0 0 | ||
| + | | 4 | ||
| + | |||
| + | |} | ||
| + | |||
| + | |||
| + | |||
| + | <br> | ||
| + | '''Ex.''' <br> | ||
| + | <math>(x_1 \or \lnot x_2 \or \ x_3 ) \and (\lnot x_1 \or \lnot \ x_3 \or x_4) \and (\ x_3 \or \ x_2 \or \lnot x_4)</math> <br> | ||
| + | [[ไฟล์:11.png]] | ||
| + | |||
| + | จะกล่าวว่าปัญหา A สามารถตรวจคำตอบได้อย่างมีประสิทธิภาพ (Efficiently certifiable) | ||
| + | ถ้ามี Algorithm V ที่ทำงานใน Polynomial time | ||
| + | * ที่ทุกๆ Yes - instance x ของ A มี Certificate C ที่ | ||
| + | |C| = poly (|X|) และ V (x,c) = 1 | ||
| + | * ที่ทุกๆ No - instance x ของ A สำหรับทุกๆ Certificate C ที่ | ||
| + | V(x,c) = 0 | ||
| + | |||
| + | |||
| + | [[ไฟล์:22.png]] | ||
| + | |||
| + | ''' Decision Problems (ปัญหาที่ตอบ yes/no) ''' | ||
| + | |||
| + | |||
| + | '''P (Polynomial)''' | ||
| + | |||
| + | ปัญหา A จะอยู่ในกลุ่ม P | ||
| + | |||
| + | ถ้ามี Algorithm ที่ทำงานใน Polynomial time ที่แก้ ปัญหา A | ||
| + | |||
| + | |||
| + | '''NP (Nondeterministic Polynomial)''' | ||
| + | ปัญหา A จะอยู่ในกลุ่ม NP | ||
| + | |||
| + | ถ้า A สามารถตรวจคำตอบได้อย่างมีประสิทธิภาพ | ||
| + | |||
| + | |||
| + | '''ตัวอย่าง SAT อยู่ใน NP''' | ||
| + | Algorithm V ที่รับ CNF <math>\varnothing</math> | ||
| + | |||
| + | และ assignment เป็น certificate จะสามารถตรวจคำตอบของปัญหาได้โดย | ||
| + | |||
| + | ถ้า <math>\varnothing</math> ทำให้เป็นจริงได้ จะมี assignment ที่ทำให้ V ตอบ Yes | ||
| + | |||
| + | แต่ ถ้า <math>\varnothing</math> ไม่สามารถทำให้เป็นจริงได้ ไม่ว่าจะใช้ assignment ได้ V จะตอบ No เสมอ | ||
| + | |||
| + | |||
| + | '''ปัญหา Composite''' | ||
| + | ให้จำนวนเต็ม N , N เป็นจำนวนประกอบหรือไม่ | ||
| + | |||
| + | พิสูจน์ว่า Composite เป็น NP | ||
| + | |||
| + | (ต้องมี 2 อย่าง คือ Certificate , Verificate) | ||
| + | |||
| + | *ให้ตัวประกอบ 2 ตัว x,y ของ N เป็น Certificate | ||
| + | |||
| + | *Algorithm V ที่ตรวจคำตอบ คำนวน x,y และ ตรวจว่าเท่ากับ N หรือไม่ | ||
| + | |||
| + | |||
| + | '''นิยาม''' ปัญหา A เป็น NP - hard ก็ต่อเมื่อ | ||
| + | |||
| + | สำหรับทุกๆ ปัญหา B ที่เป็น NP | ||
| + | |||
| + | B <math>\leqslant</math> P A | ||
| + | |||
| + | |||
| + | '''นิยาม''' ปัญหา A เป็น NP - Complete ก็ต่อเมื่อ | ||
| + | 1 A ต้องเป็น NP | ||
| + | 2 A เป็น NP-hard | ||
| + | |||
| + | |||
| + | [[ไฟล์:33.png]] | ||
| + | |||
| + | |||
| + | |||
| + | '''Cook - Lavin''' | ||
| + | SAT เป็น NP-Complete | ||
| + | *ถ้า A <math>\leqslant</math>p B และ B <math>\leqslant</math>p C แล้ว A <math>\leqslant</math>p C ด้วย | ||
| + | |||
| + | *ถ้า A เป็น NP-Complete และ A <math>\leqslant</math>p B ได้ B เป็น NP-Hard | ||
| + | |||
| + | จะพิสูจน์ ปัญหา A เป็น NP-Complete (มี 2 ขั้น) | ||
| + | 1 พิสูจน์ว่า A เป็น NP | ||
| + | 2 หาปัญหา NP-Complete B , แล้วพิสูจน์ B <math>\leqslant</math>p A | ||
| + | |||
| + | [[ไฟล์:44.png]] | ||
รุ่นแก้ไขปัจจุบันเมื่อ 19:22, 8 ตุลาคม 2553
จดบันทึกคำบรรยายโดย:
นายเสกสิทธิ์ สุวรรณ รหัสนักศึกษา 5214550332
นางสาวสลิตตา นกขุนทอง รหัสนักศึกษา 5214550308
NP Complete
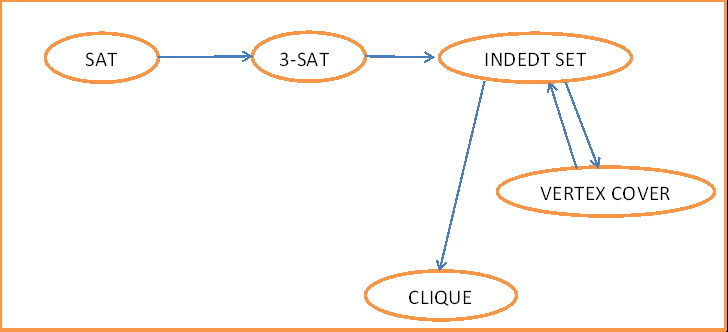
ปัญหา A P (Polynomail time to) ปัญหา B ถ้า มี poly-time algo ที่สำหรับทุกๆ instance x ของ A
x' = T(x) , | x' | = poly (| x |)
และถ้า x เป็น yes instance ของ A , x' เป็น yes-instance ของ B
x เป็น no instance ของ A , เป็น no-instance ของ B
THM: 3-SAT p INDEP-SET
Proof: ให้ เป็น 3-CNF ใดๆ
และ m clause เรียกเป็น จะสร้างกราฟได้ดังนี้
- ในแต่ละ clause สร้างสามเหลี่ยมที่ประกอบไปด้วยโหนดตัวแปรที่ปรากฎใน C ได้กราฟที่มี 3 โหนด ตามรูป
สำหรับทุกตัวแปร เชื่อมทุกโหนดที่แทนตัวแปร กับทุกโหนดที่แทน
สังเกตุว่าขั้นตอนดังกล่าวสามารถทำให้เป็น polynomial time ได้และกราฟที่ได้มีขนาดเป็น poly ในขนาด
พิสูจน์
1. ถ้า Satisfiable ,G มี independent set ขนาด m นั้นคือ มี assignment ให้กับตัวแปร
ที่ทำให้ทุก clause เป็นจริงพร้อมกัน
เนื่องจาก Ci เป็นจริงจะมีตัวแบ่งอย่างน้อย 1 ตัวใน Ci เป็นจริง,เลือกโหนดใน G ที่สอดคล้องกับตัวแปรตัวนั้นใส่ Set I โดยที่ Set I ที่มีสมาชิก M ตัว
จะพิสูจน์ว่า I เป็น Independent set ใน G
assume ว่า I ไม่เป็น independent Set นั้นคือเชื่อมระหว่างบางคู่ของโหนด u,v I
เนื่องจากเชต I มีโหนดเพียงโหนดเดียวจากแต่ละสามเหลี่ยมดังนั้นไม่มีทางที่เส้นเชื่อมดังกล่าวจะเป็นเส้นเชื่อมในสามเหลี่ยมได้
ดังนั้น ต้องเป็นเส้นเชื่อมระหว่างตัวแปร Xi บางตัวกับ เนื่องจากเราเลือกตัวแปรจาก assign ที่เป็นจริง กรณีที่ป็นไปไม่ได้
นั้นคือ I เป็น Independent set ในกราฟมีขนาด m
x1 = T , x2 = T ,x3 = F , x4 = T
Ex สมมุติมี formular
วาดกราฟได้ดังรูป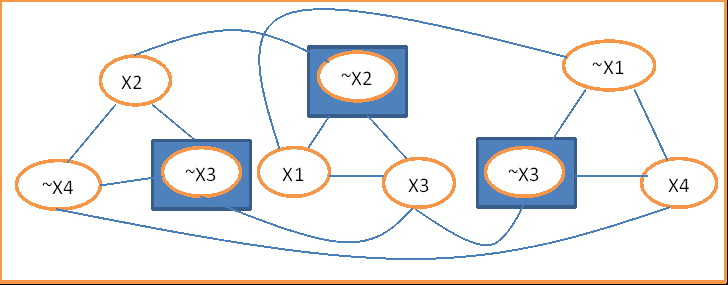
พิสูจน์ x1= T, x2=T , x3 = F ,x4 = T ให้เป็นจริง
สูจน์ให้ได้ว่า clause 1.เป็นจริง
2.เป็นจริง
3.เป็นจริง
2.ถ้า G มี independent Set ขนาด m แล้ว Satisfiable
SUBSET SUM
ในเซต A = {x1,x2,x3,..,xn} จำนวนเต็ม
มี subset B \subseteq A ที่
ต้องการพิสูจน์ว่า
thm: 3-SAT subset-sum
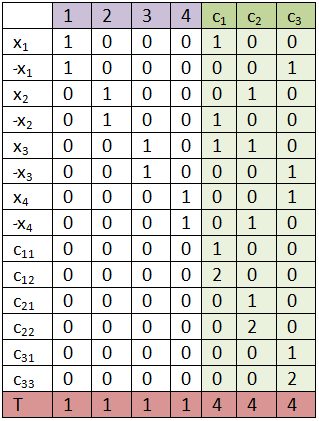
Ex.
จะได้ว่า
| C | ||
|---|---|---|
| x1 | 1 0 0 0 0 | 1 |
| x1 | 1 0 0 0 0 | 0 |
| x2 | 0 1 0 0 0 | 0 |
| x2 | 0 1 0 0 0 | 1 |
| x3 | 0 0 1 0 0 | 1 |
| x3 | 0 0 1 0 0 | 0 |
| 1 1 1 0 0 | 4 |
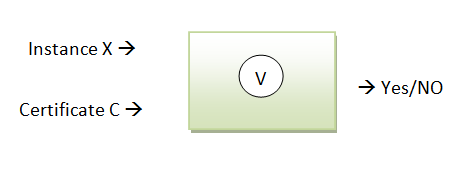
จะกล่าวว่าปัญหา A สามารถตรวจคำตอบได้อย่างมีประสิทธิภาพ (Efficiently certifiable) ถ้ามี Algorithm V ที่ทำงานใน Polynomial time
- ที่ทุกๆ Yes - instance x ของ A มี Certificate C ที่
|C| = poly (|X|) และ V (x,c) = 1
- ที่ทุกๆ No - instance x ของ A สำหรับทุกๆ Certificate C ที่
V(x,c) = 0
Decision Problems (ปัญหาที่ตอบ yes/no)
P (Polynomial)
ปัญหา A จะอยู่ในกลุ่ม P
ถ้ามี Algorithm ที่ทำงานใน Polynomial time ที่แก้ ปัญหา A
NP (Nondeterministic Polynomial)
ปัญหา A จะอยู่ในกลุ่ม NP
ถ้า A สามารถตรวจคำตอบได้อย่างมีประสิทธิภาพ
ตัวอย่าง SAT อยู่ใน NP
Algorithm V ที่รับ CNF
และ assignment เป็น certificate จะสามารถตรวจคำตอบของปัญหาได้โดย
ถ้า ทำให้เป็นจริงได้ จะมี assignment ที่ทำให้ V ตอบ Yes
แต่ ถ้า ไม่สามารถทำให้เป็นจริงได้ ไม่ว่าจะใช้ assignment ได้ V จะตอบ No เสมอ
ปัญหา Composite
ให้จำนวนเต็ม N , N เป็นจำนวนประกอบหรือไม่
พิสูจน์ว่า Composite เป็น NP
(ต้องมี 2 อย่าง คือ Certificate , Verificate)
- ให้ตัวประกอบ 2 ตัว x,y ของ N เป็น Certificate
- Algorithm V ที่ตรวจคำตอบ คำนวน x,y และ ตรวจว่าเท่ากับ N หรือไม่
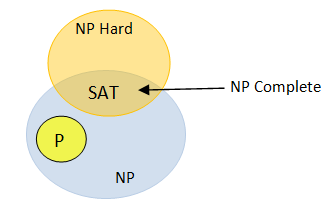
นิยาม ปัญหา A เป็น NP - hard ก็ต่อเมื่อ
สำหรับทุกๆ ปัญหา B ที่เป็น NP
B P A
นิยาม ปัญหา A เป็น NP - Complete ก็ต่อเมื่อ
1 A ต้องเป็น NP 2 A เป็น NP-hard
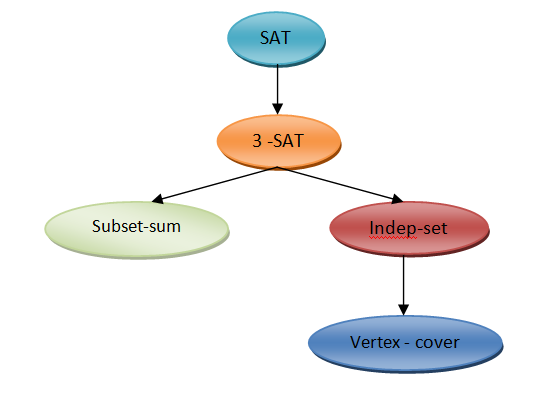
Cook - Lavin
SAT เป็น NP-Complete
- ถ้า A p B และ B p C แล้ว A p C ด้วย
- ถ้า A เป็น NP-Complete และ A p B ได้ B เป็น NP-Hard
จะพิสูจน์ ปัญหา A เป็น NP-Complete (มี 2 ขั้น)
1 พิสูจน์ว่า A เป็น NP 2 หาปัญหา NP-Complete B , แล้วพิสูจน์ B p A