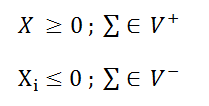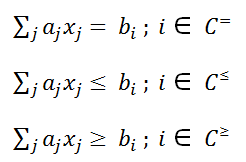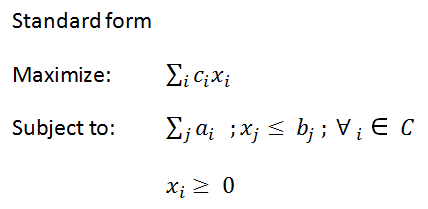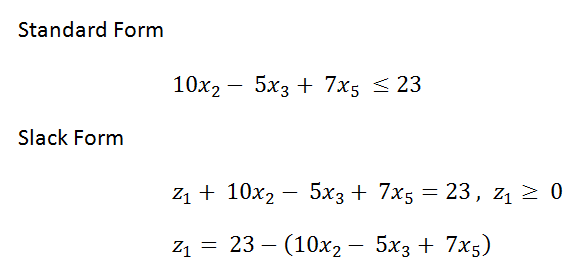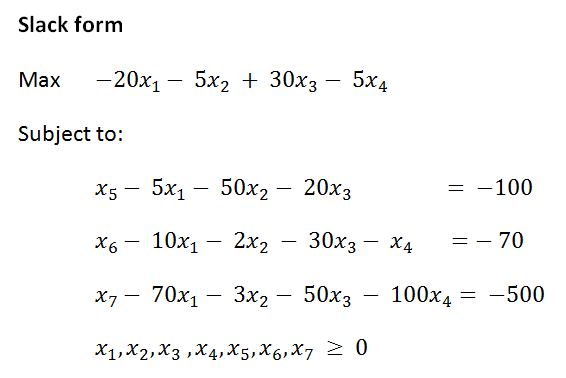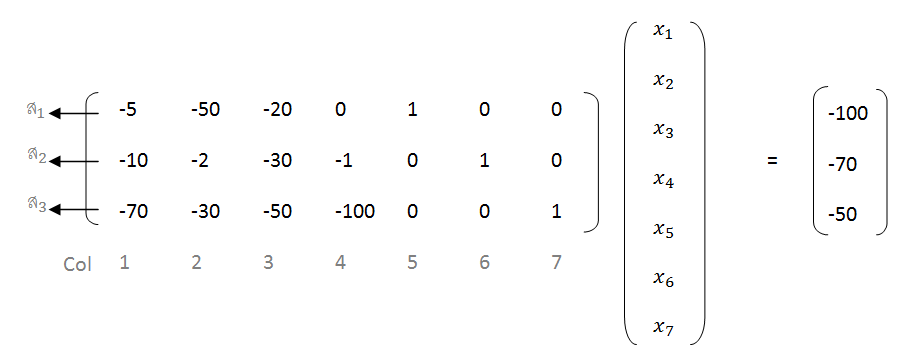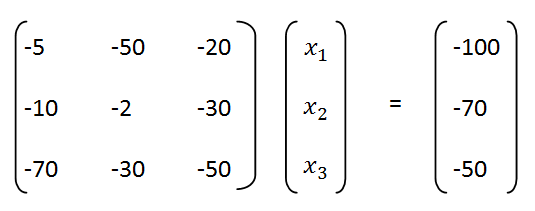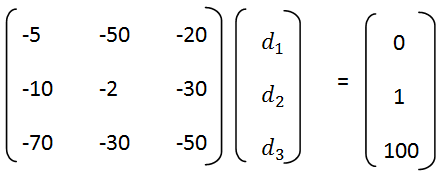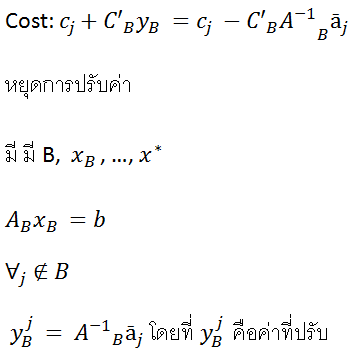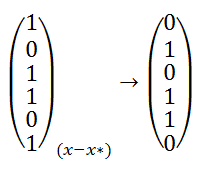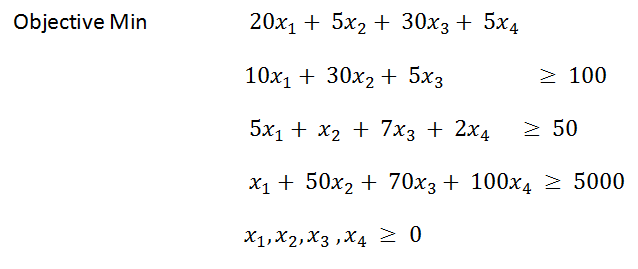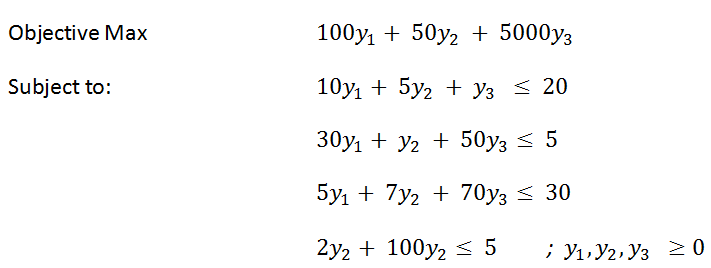ผลต่างระหว่างรุ่นของ "204512-53/lecture12"
Chatchapol (คุย | มีส่วนร่วม) (หน้าที่ถูกสร้างด้วย '== '''204512-53/lecture12''' == '''จดบันทึกคำบรรยายโดย:''' นายชัชพล นุโย…') |
Tommycpe (คุย | มีส่วนร่วม) |
||
| (ไม่แสดง 3 รุ่นระหว่างกลางโดยผู้ใช้ 3 คน) | |||
| แถว 1: | แถว 1: | ||
| − | + | '''Linear Programming''' | |
| − | |||
| − | |||
| − | |||
| − | + | กำหนดการเชิงเส้น จะอยู่ในรูปแบบทางคณิตศาสตร์ของสมการเชิงเส้นและอสมการเชิงเส้น แล้วหาค่าสูงสุด ต่ำสุดของฟังก์ชันที่สอดคล้องกับสมการ (และอสมการ) ที่กำหนด ตัวแบบคณิตศาสตร์ | |
| − | + | การหาค่าสูงสุด : Maximize <math>\sum_i{c_ix_i}</math> | |
| − | + | โดยที่มีตัวแปร 2 แบบคือ | |
| − | |||
| − | + | [[ไฟล์:Lecture12.1.gif]] | |
| − | + | และเงื่อนไข อยู่ในรูป General Form | |
| − | + | [[ไฟล์:Lecture12.2.gif]] | |
| − | + | [[ไฟล์:Lecture12.3.gif]] | |
| − | + | แปลงเป็น Minimum โดยการแปลงค่า <math>\sum_i{c_ix_i}</math> โดยการคูณเครื่องหมายลบเข้าไปจะทำให้เปลี่ยนเครื่องหมายของอสมการเปลี่ยนไปในทางตรงข้าม | |
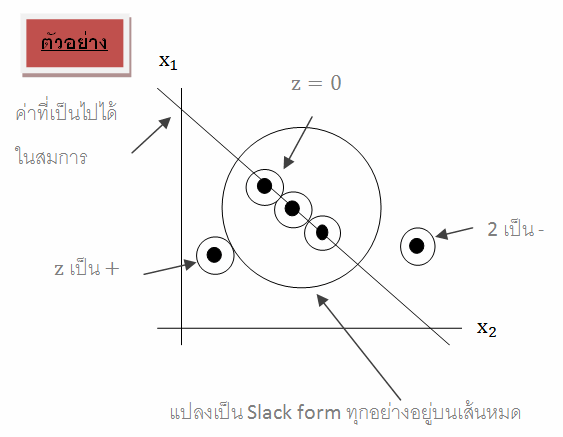
| − | + | การคิดคำนวณด้วยวิธีการ Simplex ต้องเปลี่ยนระบบอสมการในโมเดลคณิตศาสตร์เชิงเส้นให้อยู่ในรูปของสมการเพื่อความง่ายต่อการคำนวณ โดยเพิ่มตัวแปรสมมติขึ้น รูปแบบของสมการจะขยายเพิ่มเติมขึ้นเราเรียกรูปแบบนี้ว่า “Slack Form” | |
| − | + | [[ไฟล์:Lecture12.4.gif]] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | [[ไฟล์: | + | [[ไฟล์:Algorhw1.gif]] |
| − | + | หลักการเพิ่มตัวแปรใน Slack Form | |
| + | 1. ในอสมการเดิมที่อยู่ในรูปเครื่องหมายน้อยกว่าหรือเท่ากับ เราจะเปลี่ยนเป็นเครื่องหมายเท่ากับ ดังนั้น จึงต้องเพิ่มส่วนที่เหลือโดยการเพิ่มค่าเข้าไปอีก โดยตัวแปรที่เพิ่มค่าจึงมีเครื่องหมาย + นำหน้า เพื่อให้เหมือนกับว่าเพิ่มค่าให้ได้เท่ากับ | ||
| + | 2. ในกรณีของอสมการในโมเดลคณิตศาสตร์เดิมอยู่ในรูปเครื่องหมายมากกว่าหรือเท่ากับ เปรียบว่าฝั่งซ้ายมากกว่าฝั่งขวา ดังนั้นการเปลี่ยนอสมการให้เป็นสมการจึงต้องลดลง ในที่นี้ต้องเติมตัวแปร Slack โดยมีเครื่องหมายลบนำหน้า แต่จากหลักการคำนวณทางแมทริกซ์ ตัวแปรที่ให้ผลลัพธ์แต่ละครั้งที่คำนวณหา จะมีสัมประสิทธิ์เท่ากับ + 1 ซึ่งเกิดเป็นแมทริกซ์ของสัมประสิทธิ์ของตัวแปรที่เป็นตัวแปรพื้นฐาน (basic variable) ตามข้อกำหนดของวิธีซิมเพล็กซ์ กำหนดว่า ผลลัพธ์เบื้องต้นที่เป็นไปได้จะมีค่าตัวแปรที่เป็นตัวแปรพื้นฐานมากกว่าหรือเท่ากับศูนย์ ดังนั้น จึงต้องเติมตัวแปรอีกตัวหนึ่งที่มีสัมประสิทธิ์เป็นบวก | ||
| + | 3. ในกรณีที่เป็นสมการที่มีเครื่องหมาย เท่ากับ = อยู่แล้ว ให้เพิ่มตัวแปรได้เลย | ||
| − | + | ปัญหา เทพวิตามิน คนต้องการ | |
| + | <math> v_A</math> 100 มก. | ||
| + | <math> v_B 70</math> มก. | ||
| + | <math> v_C</math> 500 มก. | ||
| − | + | [[ไฟล์:Lecture12.5.gif]] | |
| − | + | [[ไฟล์:Lecture12.6.gif]] | |
| − | + | [[ไฟล์:Lecture12.7.gif]] | |
| − | + | [[ไฟล์:Lecture12.8.gif]] | |
| − | + | แปลงให้อยู่ในรูป Matrix | |
| − | + | [[ไฟล์:Algorhw2.gif]] | |
| − | + | ใน Case นี้ให้ <math> x_4=0</math> | |
| − | + | [[ไฟล์:Algorhw3.gif]] | |
| − | + | <math>x_1= 235/36 ,x_2= 96/72 , x_3= 5/42</math> | |
| − | + | สังเกตุที่ <math>x_3</math> เพิ่ม<math> x_4</math> ไปแล้ว <math>x_3</math> มีค่าเพิ่มขึ้นเรื่อยๆ ซึ่งไม่มีผลอะไรเพราะมีค่ามากกว่าเท่ากับ 0 อยู่แล้ว | |
| − | + | จากโจทย์ถ้าเพิ่ม <math>x_4</math> จะมีผลกับ ส<math> _2</math> (-1) และ ส<math>_3</math> (-100) | |
| − | + | [[ไฟล์:Algorhw5.gif]] | |
| − | |||
| − | |||
| − | + | แก้สมการเมตริกซ์จะได้ | |
| − | + | <math> | |
| + | d_1= (-131)/72 ,d_2= (-7)/144 , d_3= 83/144</math> | ||
| − | + | เพิ่ม <math>x_4</math> ไป <math>235/36 × 72/131=3.588</math> ซึ่งจะทำให้ค่า <math>x_1</math> เป็น 0 | |
| + | เพิ่ม <math>x_4</math> ไป <math>95/72 × 144/7=27.14</math> ซึ่งจะทำให้ค่า <math> x_2</math> เป็น 0 | ||
| − | + | กำหนด x1, x2, x3 ซึ่งเรียกว่า Basic Solution ที่เป็น matrix | |
| − | + | Max C’x | |
| − | + | Subject to | |
| − | + | Ax = b | |
| + | x ≥ 0 | ||
| + | เลือก B = {1,2,3} | ||
| − | + | [[ไฟล์:Lecture12.9.gif]] | |
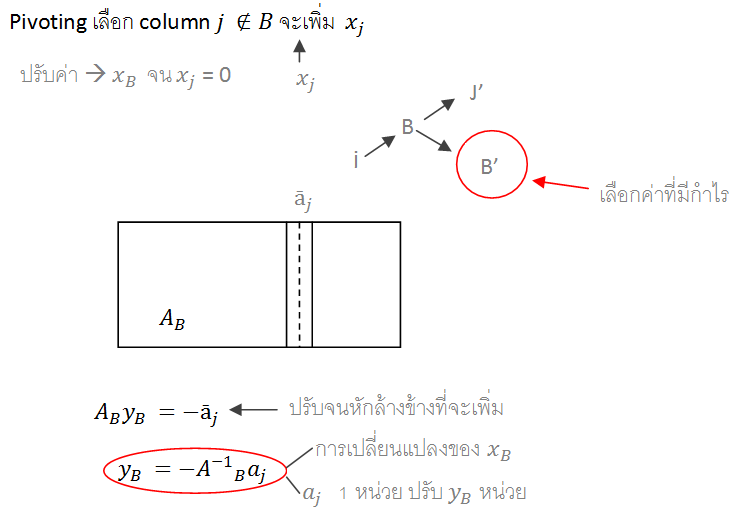
| − | + | โดยที่ C’ = เวกเตอร์แนวนอน, X = เวกเตอร์แนวตั้ง, A = คือ matrix มี ‘ เป็นแถวเวกเตอร์ ไม่มี ‘ เป็นหลักเวกเตอร์ , <math>A_B</math> = Matrix A ที่หยิบมาเฉพาะหลักในเซต B , <math>X_B</math> = เอาเฉพาะตัวแปรใน index B | |
| − | |||
| − | |||
| + | [[ไฟล์:Algorhw4.gif]] | ||
| − | + | เริ่มจาก basic feasible solution XB มี B เป็นเซตของ basis | |
| − | + | <math>A_BX_B = b</math> | |
| − | + | [[ไฟล์:Algorhw6.gif]] | |
| + | [[ไฟล์:Lecture12.10.gif]] | ||
| − | + | ||
| + | ถ้า <math> C_j+ C'_B y_B^i≤0</math> แสดงว่าปรับแล้วค่าไม่ดีขึ้น หยิบ field ไหนก็ได้ < 0 | ||
| + | พิจารณา x ใดๆ ที่เป็น Basis Feasible Solution | ||
| + | |||
| + | Ax = b | ||
| + | x ≥ 0 | ||
| + | |||
| + | [[ไฟล์:Lecture12.11.gif]] | ||
| + | |||
| + | พิจารณา x’b ใดๆ ที่เป็น Basis Physical Solution | ||
| + | Ax = b | ||
| + | x ≥ 0 | ||
| + | |||
| + | [[ไฟล์:Algorhw8.gif]] | ||
| + | |||
| + | เกมส์วิตามิน (ต่อ) : ในกรณีที่ต้องการกินวิตามินให้ได้ครบ | ||
| + | |||
| + | [[ไฟล์:Lecture12.12.gif]] | ||
| + | |||
| + | มองในแง่คนขาย ถ้าต้องการขายวิตามินให้ได้ราคาดีที่สุด | ||
| + | |||
| + | [[ไฟล์:lecture12.13.gif]] | ||
| + | |||
| + | เป็นการแปลงจากแถวเป็นหลักและทำให้ Objective เปลี่ยนไปซึ่งคุณสมบัตินี้เราเรียกว่า Dual Linear Programing | ||
| + | |||
| + | นฤดล ขจรวุฒิตระกูล 5214550154 | ||
| + | รัตนพงษ์ ชัยรักษ์วัฒนา 5214550243 | ||
| + | ศักดา เอื้อจิรกาล 5214550286 | ||
| + | สยาม ชุณห์วิจิตรา 5214550294 | ||
| + | สุเกติองค์ ภู่พัฒน์ 5214550316 | ||
รุ่นแก้ไขปัจจุบันเมื่อ 16:21, 31 ตุลาคม 2553
Linear Programming
กำหนดการเชิงเส้น จะอยู่ในรูปแบบทางคณิตศาสตร์ของสมการเชิงเส้นและอสมการเชิงเส้น แล้วหาค่าสูงสุด ต่ำสุดของฟังก์ชันที่สอดคล้องกับสมการ (และอสมการ) ที่กำหนด ตัวแบบคณิตศาสตร์
การหาค่าสูงสุด : Maximize
โดยที่มีตัวแปร 2 แบบคือ
และเงื่อนไข อยู่ในรูป General Form
แปลงเป็น Minimum โดยการแปลงค่า โดยการคูณเครื่องหมายลบเข้าไปจะทำให้เปลี่ยนเครื่องหมายของอสมการเปลี่ยนไปในทางตรงข้าม
การคิดคำนวณด้วยวิธีการ Simplex ต้องเปลี่ยนระบบอสมการในโมเดลคณิตศาสตร์เชิงเส้นให้อยู่ในรูปของสมการเพื่อความง่ายต่อการคำนวณ โดยเพิ่มตัวแปรสมมติขึ้น รูปแบบของสมการจะขยายเพิ่มเติมขึ้นเราเรียกรูปแบบนี้ว่า “Slack Form”
หลักการเพิ่มตัวแปรใน Slack Form 1. ในอสมการเดิมที่อยู่ในรูปเครื่องหมายน้อยกว่าหรือเท่ากับ เราจะเปลี่ยนเป็นเครื่องหมายเท่ากับ ดังนั้น จึงต้องเพิ่มส่วนที่เหลือโดยการเพิ่มค่าเข้าไปอีก โดยตัวแปรที่เพิ่มค่าจึงมีเครื่องหมาย + นำหน้า เพื่อให้เหมือนกับว่าเพิ่มค่าให้ได้เท่ากับ 2. ในกรณีของอสมการในโมเดลคณิตศาสตร์เดิมอยู่ในรูปเครื่องหมายมากกว่าหรือเท่ากับ เปรียบว่าฝั่งซ้ายมากกว่าฝั่งขวา ดังนั้นการเปลี่ยนอสมการให้เป็นสมการจึงต้องลดลง ในที่นี้ต้องเติมตัวแปร Slack โดยมีเครื่องหมายลบนำหน้า แต่จากหลักการคำนวณทางแมทริกซ์ ตัวแปรที่ให้ผลลัพธ์แต่ละครั้งที่คำนวณหา จะมีสัมประสิทธิ์เท่ากับ + 1 ซึ่งเกิดเป็นแมทริกซ์ของสัมประสิทธิ์ของตัวแปรที่เป็นตัวแปรพื้นฐาน (basic variable) ตามข้อกำหนดของวิธีซิมเพล็กซ์ กำหนดว่า ผลลัพธ์เบื้องต้นที่เป็นไปได้จะมีค่าตัวแปรที่เป็นตัวแปรพื้นฐานมากกว่าหรือเท่ากับศูนย์ ดังนั้น จึงต้องเติมตัวแปรอีกตัวหนึ่งที่มีสัมประสิทธิ์เป็นบวก 3. ในกรณีที่เป็นสมการที่มีเครื่องหมาย เท่ากับ = อยู่แล้ว ให้เพิ่มตัวแปรได้เลย
ปัญหา เทพวิตามิน คนต้องการ 100 มก. มก. 500 มก.
แปลงให้อยู่ในรูป Matrix
ใน Case นี้ให้
สังเกตุที่ เพิ่ม ไปแล้ว มีค่าเพิ่มขึ้นเรื่อยๆ ซึ่งไม่มีผลอะไรเพราะมีค่ามากกว่าเท่ากับ 0 อยู่แล้ว
จากโจทย์ถ้าเพิ่ม จะมีผลกับ ส (-1) และ ส (-100)
แก้สมการเมตริกซ์จะได้
เพิ่ม ไป ซึ่งจะทำให้ค่า เป็น 0 เพิ่ม ไป ซึ่งจะทำให้ค่า เป็น 0
กำหนด x1, x2, x3 ซึ่งเรียกว่า Basic Solution ที่เป็น matrix Max C’x Subject to Ax = b x ≥ 0 เลือก B = {1,2,3}
โดยที่ C’ = เวกเตอร์แนวนอน, X = เวกเตอร์แนวตั้ง, A = คือ matrix มี ‘ เป็นแถวเวกเตอร์ ไม่มี ‘ เป็นหลักเวกเตอร์ , = Matrix A ที่หยิบมาเฉพาะหลักในเซต B , = เอาเฉพาะตัวแปรใน index B
เริ่มจาก basic feasible solution XB มี B เป็นเซตของ basis
ถ้า แสดงว่าปรับแล้วค่าไม่ดีขึ้น หยิบ field ไหนก็ได้ < 0
พิจารณา x ใดๆ ที่เป็น Basis Feasible Solution
Ax = b x ≥ 0
พิจารณา x’b ใดๆ ที่เป็น Basis Physical Solution Ax = b x ≥ 0
เกมส์วิตามิน (ต่อ) : ในกรณีที่ต้องการกินวิตามินให้ได้ครบ
มองในแง่คนขาย ถ้าต้องการขายวิตามินให้ได้ราคาดีที่สุด
เป็นการแปลงจากแถวเป็นหลักและทำให้ Objective เปลี่ยนไปซึ่งคุณสมบัตินี้เราเรียกว่า Dual Linear Programing
นฤดล ขจรวุฒิตระกูล 5214550154 รัตนพงษ์ ชัยรักษ์วัฒนา 5214550243 ศักดา เอื้อจิรกาล 5214550286 สยาม ชุณห์วิจิตรา 5214550294 สุเกติองค์ ภู่พัฒน์ 5214550316