204512/บรรยาย 2

เกริ่นนำ

หลักการของ Divide and Conquer Algorithm ประกอบไปด้วย 3 ส่วนดังนี้

1.แตกย่อยปัญหาเป็นชิ้นเล็ก หลายชิ้น

2.ทำการแก้ปัญหาย่อยเหล่านี้ด้วยวิธีการที่คล้ายกัน

3.คำตอบสุดท้ายหาได้จากการสรุปคำตอบทั้งหมดของทุกปัญหาย่อย

ดังจะเห็นได้จากปัญหาทั้งในชีวิตประจำวัน และปัญหาทางทฤษฎีคอมพิวเตอร์ สามารถเปรียบเทียบกรรมวิธี Divide and Conquer Algorithm กับ Lagacy Algorithm ได้ว่ามีประสิทธิ์ภาพต่างกันมากน้อยเพียงใด ซึ่งวิธีที่เปรียบเทียบเป็นที่นิยมโดยทั่วไปคือการหา Big O Notation มาเปรียบเทียบกัน

---

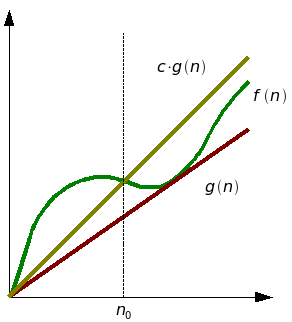
การวิเคราะห์เปรียบเทียบ Algorithm โดยการหา Big O Notation

Definition 1

$\ T(n)=O(f(n))$ 

T of n is in Big-Oh of f of n iff there're constants $\ c$ and $\ n_{0}$ such that 

$\ T(n)\leq c\cdot f(n)$ for all $\ n\geq n_{0}$

กราฟแสดงตัวอย่าง Big-Oh ตามนิยาม

เช่น

$\ 3n^{2}+2n=O(n^{2})$

จะเห็นได้ว่า definition 1 เป็นจริงได้เมื่อ $\ C=4,n_{0}=2$
$\ 3n^{2}+2n\leq c\cdot n^{2}$
$\ 3n^{2}+2n\leq 3n^{2}+n^{2}$

โดยทั่วไปแล้ว Big-Oh คือการแสดง Upper Bound ของฟังก์ขั่น ขณะที่ Big-Omega ($\Omega$) เป็นการแสดงถึง Lower Bound ของฟังก์ชั่น

---

ตัวอย่างปัญหา ที่ใช้กรรมวิธีแก้ไขแบบ Divide & Conquer

Multiplication

การคูณกันของ $\ x\cdot y$ ที่เป็น binary number ขนาด n-bit สามารถแยกออกได้เป็น

$\ x\cdot y=(2^{\frac {n}{2}}x_{L}+x_{R})\cdot (2^{\frac {n}{2}}y_{L}+y_{R})$

$\ x\cdot y=2^{n}x_{L}y_{L}+2^{\frac {n}{2}}(x_{L}y_{R}+y_{L}x_{R})+x_{R}y_{R}$

• สามารถสังเกตได้ว่า ประกอบไปด้วยพจน์ที่คูณกัน 4 ชุด

นิยาม Function ของเวลาที่ใช้ในการคำนวณตัวเลข n-bit เป็น $T(n)=2T({\frac {n}{2}})+O(n)$

---

แหล่งข้อมูล​อื่น​

อธิบายเรื่อง Big-O-Notation ของ Wiki Pedia อธิบายเรื่อง Big-O-Notation ของ Wiki Pedia

ใช้ยากจังน้อ