ผลต่างระหว่างรุ่นของ "204512/บรรยาย 3"
Patcharin (คุย | มีส่วนร่วม) |
Patcharin (คุย | มีส่วนร่วม) |
||
| แถว 46: | แถว 46: | ||
สมมติว่ามี data 1,2,8,3,7,5,10,20,12 เขียนเป็น Binary Search Tree ได้ดังนี้ <br /> | สมมติว่ามี data 1,2,8,3,7,5,10,20,12 เขียนเป็น Binary Search Tree ได้ดังนี้ <br /> | ||
[[ภาพ:bst_1.jpg]] | [[ภาพ:bst_1.jpg]] | ||
| + | ---- | ||
| + | == AVL Tree == | ||
| + | AVL (Adelson-Velskii and Landis) tree คือ binary search tree ที่มีเงื่อนไขของความสมดุล (Balance Condition) โดยเงื่อนไขดังกล่าวคือ | ||
| + | Condition: ในทุกๆ โหนด ความสูงของทางด้ายซ้ายและด้านขวาต่างกันไม่เกิน 1 โดยที่ให้ N(k) แทนจำนวนโหนดที่น้อยที่สุดใน AVL Tree ที่มีความสูง k | ||
| + | <br /> | ||
| + | [[ภาพ:bst_2.jpg]] | ||
| + | <br /> | ||
| + | จากเงื่อนไขของ AVL Tree จะสรุปได้ | ||
| + | N(1) = 1, N(2) = 2 | ||
| + | N(k) = N(k-1) + N(k-2) + 1 | ||
| + | จะสังเกตได้ว่ามีลักษณะเป็น Fibonacci แต่มีการบวก 1 เข้ามาด้วย | ||
| + | |||
| + | จากสมการข้างต้น | ||
| + | N(k) = N(k-1) + N(k-2) + 1 | ||
| + | |||
| + | N(k) = N(k-2) + N(k-3) + N(k-2) + 1<br /> | ||
| + | ≥ 2N(k-2)<br /> | ||
| + | ≥ (<math>2</math>)k <br /> | ||
| + | ≥ (<math>{2^{k/2}}</math>) ---* | ||
| + | <br /> | ||
| + | จะสังเกตได้ว่าฟังก์ชันดังกล่าวมีขนาดเป็น Exponential ใน k <br /> | ||
| + | สรุป: AVL Tree ที่มี n โหนดจะมีความสูง O(log n) <br /> | ||
| + | === การหมุนของ AVL Tree === | ||
| + | การหมุน (Rotation) ของ AVL Tree กระทำเพื่อให้ต้นไม่ที่ไม่อยู่ในเงื่อนไขของ AVL Tree กลับเข้ามาอยู่ในเงื่อนไข ซึ่งมีรูปแบบการทำงานดังนี้ | ||
| + | *Single Rotation | ||
| + | **การหมุนทางขวา (Right Rotation) | ||
| + | **การหมุนทางซ้าย (Left Rotation) | ||
| + | *Double Rotation | ||
รุ่นแก้ไขเมื่อ 09:34, 24 มิถุนายน 2550
ความรู้เบื้องต้น
Tree เป็นโครงสร้างชนิดไม่เชิงเส้น (Non-linear) มีลักษณะเป็น recursive ประกอบไปด้วยสมาชิกที่เรียกว่า Node และมีเส้นที่เชื่อมระหว่าง Node ที่เรียกว่า branch คำสำคัญที่เกี่ยวกับ Tree มีดังนี้
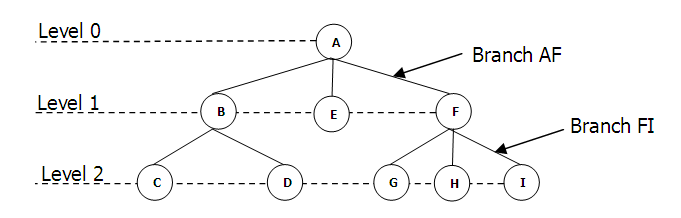
| Root Node: A | Sibling Node: {B, E, F}, {C, D}, {G, H, I} |
| Parents Node: A, B, F | Leaves Node: C, D, E, G, H, I |
| Child Node: B, E, F, C, D, G, H, I | Internal Node: B, F |
- Root Node คือ โหนดที่อยู่บนสุดของต้นไม้
- Leaf Node คือ โหนดที่ไม่มีลูกหรือโหนดอื่นต่อ เรียกอีกอย่างหนึ่งว่า External Node
- Internal Node คือ โหนดที่ไม่ใช่ Root และ Leaf Node
- Depth คือ ความยาวจาก Root node ถึง Node ที่สนใจ
- Height คือ ความยาวจาก Node ที่สนใจถึง Leaf Node ที่ลึกที่สุดที่มี Node ที่สนใจเป็น Parent
| A | 0 | 2 |
| B | 1 | 1 |
| C | 2 | 0 |
| D | 2 | 0 |
| E | 1 | 0 |
| F | 1 | 1 |
| G | 2 | 0 |
| H | 2 | 0 |
| I | 2 | 0 |
Binary Search Tree
Binary Search Tree เป็นขั้นตอนวิธีการทำงานที่สำคัญของ Binary Tree โดยจะสนับสนุนการทำงานดังต่อไปนี้
- Find (key)
- Insert (key)
- Delete (key)
ซึ่งเวลาที่ใช้ในการค้นหานั้นจะขึ้นอยู่กับความสูงของต้นไม้ โดยถ้ามีข้อมูล n ตัวความสูงของต้นไม้จะลึกไปกว่า O(log n)
สมมติว่ามี data 1,2,8,3,7,5,10,20,12 เขียนเป็น Binary Search Tree ได้ดังนี้
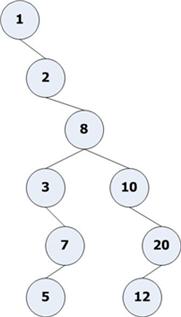
AVL Tree
AVL (Adelson-Velskii and Landis) tree คือ binary search tree ที่มีเงื่อนไขของความสมดุล (Balance Condition) โดยเงื่อนไขดังกล่าวคือ
Condition: ในทุกๆ โหนด ความสูงของทางด้ายซ้ายและด้านขวาต่างกันไม่เกิน 1 โดยที่ให้ N(k) แทนจำนวนโหนดที่น้อยที่สุดใน AVL Tree ที่มีความสูง k
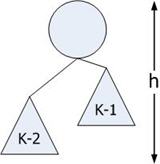
จากเงื่อนไขของ AVL Tree จะสรุปได้
N(1) = 1, N(2) = 2
N(k) = N(k-1) + N(k-2) + 1
จะสังเกตได้ว่ามีลักษณะเป็น Fibonacci แต่มีการบวก 1 เข้ามาด้วย
จากสมการข้างต้น N(k) = N(k-1) + N(k-2) + 1
N(k) = N(k-2) + N(k-3) + N(k-2) + 1
≥ 2N(k-2)
≥ ()k
≥ () ---*
จะสังเกตได้ว่าฟังก์ชันดังกล่าวมีขนาดเป็น Exponential ใน k
สรุป: AVL Tree ที่มี n โหนดจะมีความสูง O(log n)
การหมุนของ AVL Tree
การหมุน (Rotation) ของ AVL Tree กระทำเพื่อให้ต้นไม่ที่ไม่อยู่ในเงื่อนไขของ AVL Tree กลับเข้ามาอยู่ในเงื่อนไข ซึ่งมีรูปแบบการทำงานดังนี้
- Single Rotation
- การหมุนทางขวา (Right Rotation)
- การหมุนทางซ้าย (Left Rotation)
- Double Rotation