204512/บรรยาย 2

บันทึกคำบรรยายวิชา 204512 นี้ เป็นบันทึกที่นิสิตเขียนขึ้น เนื้อหาโดยมากยังไม่ผ่านการตรวจสอบอย่างละเอียด การนำไปใช้ควรระมัดระวัง

จดบันทึกคำบรรยายโดย: (กรุณาใส่ด้วย)

เกริ่นนำ

หลักการของ Divide and Conquer Algorithm ประกอบไปด้วย 3 ส่วนดังนี้

1.แตกย่อยปัญหาเป็นชิ้นเล็ก หลายชิ้น

2.ทำการแก้ปัญหาย่อยเหล่านี้ด้วยวิธีการที่คล้ายกัน

3.คำตอบสุดท้ายหาได้จากการสรุปคำตอบทั้งหมดของทุกปัญหาย่อย

ดังจะเห็นได้จากปัญหาทั้งในชีวิตประจำวัน และปัญหาทางทฤษฎีคอมพิวเตอร์ สามารถเปรียบเทียบกรรมวิธี Divide and Conquer Algorithm กับ Lagacy Algorithm ได้ว่ามีประสิทธิ์ภาพต่างกันมากน้อยเพียงใด ซึ่งวิธีที่เปรียบเทียบเป็นที่นิยมโดยทั่วไปคือการหา Big O Notation มาเปรียบเทียบกัน

---

การวิเคราะห์เปรียบเทียบ Algorithm โดยการหา Big O Notation

Definition 1

$\ T(n)=O(f(n))$ 

T of n is in Big-Oh of f of n iff there're constants $\ c$ and $\ n_{0}$ such that 

$\ T(n)\leq c\cdot f(n)$ for all $\ n\geq n_{0}$

กราฟแสดงตัวอย่าง Big-Oh ตามนิยาม

เช่น

$\ 3n^{2}+2n=O(n^{2})$

จะเห็นได้ว่า definition 1 เป็นจริงได้เมื่อ $\ C=4,n_{0}=2$
$\ 3n^{2}+2n\leq c\cdot n^{2}$
$\ 3n^{2}+2n\leq 3n^{2}+n^{2}$

โดยทั่วไปแล้ว Big-Oh คือการแสดง Upper Bound ของฟังก์ขั่น ขณะที่ Big-Omega ($\Omega$) เป็นการแสดงถึง Lower Bound ของฟังก์ชั่น

---

ตัวอย่างปัญหา ที่ใช้กรรมวิธีแก้ไขแบบ Divide & Conquer

Multiplication

การคูณกันของ $\ x\cdot y$ ที่เป็น binary number ขนาด n-bit สามารถแยกออกได้เป็น

$\ x\cdot y=(2^{\frac {n}{2}}x_{L}+x_{R})\cdot (2^{\frac {n}{2}}y_{L}+y_{R})$

$\ x\cdot y=2^{n}x_{L}y_{L}+2^{\frac {n}{2}}(x_{L}y_{R}+y_{L}x_{R})+x_{R}y_{R}$

• สามารถสังเกตได้ว่า ประกอบไปด้วยพจน์ที่คูณกัน 4 ชุด

นิยาม Function ของเวลาที่ใช้ในการคำนวณตัวเลข n-bit เป็น $T(n)=2T({\frac {n}{2}})+O(n)$

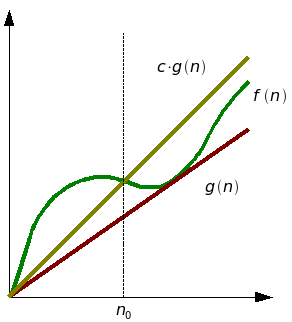
จากภาพ Tree มีความสูง $\log {n}\,$ ทำให้ได้ว่า

$T(n)=cn[1+2+4+...+2^{n}]=cn\cdot 2^{\log {n}}[{\frac {1}{2^{\log {n}}}}+...+{\frac {1}{4}}+{\frac {1}{2}}+1]={\mathcal {O}}(n^{2})$

Gauss ได้เสนอวิธีการคูณในอีกรูปแบบหนึ่งที่ใช้การคูณเพียงสามครั้งจาก $x_{L}y_{R}+x_{R}y_{L}=(x_{L}+x_{R})(y_{L}+y_{R})-x_{L}y_{L}-x_{R}y_{R}\,$ ทำให้อัลกอลิธึ่มได้รับการปรับปรุงเป็น $T(n)=3T({\frac {n}{2}})+{\mathcal {O}}(n)$ ซึ่งเมื่อคำนวณในรูปแบบเดียวกับ Tree ด้านบนโดยถือว่าแต่ละ node จะมีลูกอยู่ 3 ชุดแทนที่จะเป็น 4 ชุด เราจะได้ว่า

$T(n)=cn({\frac {3}{2}})^{\log {n}}=n^{log_{2}{3}}=n^{1.59}$

Merge Sort

Merge Sort เป็นอัลกอลิธึ่มแบบ Devide-and-Conquer อีกอันหนึ่งที่ อาศัยการแบ่งข้อมูลออกเป็นส่วนเล็กๆ แล้วเรียงลำดับให้ถูกต้อง แล้วจึงนำข้อมูลที่เรียงแล้วกลับมาต่อกัน

กระบวนการทำ Merge Sort มีสามขั้นคือ

• การแบ่งส่วนข้อมูล ได้ทำได้ทันที
• การเรียงข้อมูล ที่แบ่งไปครึ่งๆ แล้ว ใช้เวลา $T({\frac {n}{2}})\,$
• การนำข้อมูลที่เรียงแล้วสองชุดมาต่อกันใช้เวลา ${\mathcal {O}}(n)$

โดยรวมแล้ว Merge Sort ใช้เวลาในการทำงาน $T(n)=T({\frac {n}{2}})+{\mathcal {O}}(n)$

หรือก็คือ ${\mathcal {O}}(n\log {n})$

Fast Furier Transform

กราฟแสดงการหาสมการผลลัพธ์จากการคูณค่าในแต่ละจุดของสมการตั้งต้น ภาพจากWalterzorn.com

FFT คืออัลกอลิธึ่มที่ใช้ในการหาผลคูณของสมการ Polynomial สองชุดเข้าด้วยกัน เพื่อใช้งานในด้าน Signal บางอย่าง โดยมีแนวคิดคือการหาสมการที่เป็นผลคุณของ Polynomial นั้นไม่จำเป็นที่จะต้องเกิดจากการนำสมการมาคุณกันจริงๆ แต่อาจสร้างได้จากคุณสมบัติของ Polynomial ดังนี้

• สมการ Polynomial ที่มี degree เป็น d ใดๆ สามารถสร้างขึ้นจากการหาค่าผลของสมการที่ตำแหน่งต่างๆ จำนวน d+1 ตำแหน่ง
• เมือนำสมการ Polynomial degree d สองสมการมาคูณกัน เราจะได้สมการ Polynomial degree เป็น 2d
• ดังนั้นหากเราหาค่าของสมการตั้งต้นสองสมการจำนวน 2d+1 จุด แล้วนำมาคูณกัน สุดท้ายแล้วเราจะได้ค่า 2d+1 จุดที่สามารถนำไป Interpolate กลับมาเป็นสมการผลคูณของ Polynomial สองสมการได้

Devide and Conconquer

เริ่มจากพิจารณาสมการ Polynomial degree-n ใดๆ เช่น $f(x)=8+5x+4x^{2}+2x^{3}\,$ เราสามารถหาค่าของจุดต่างๆ จำนวน n จุดได้ โดยหาค่าทั้งในฝั่งบวกและลบไปพร้อมๆ กัน เช่นพิจารณาจุด $\pm x_{1},\pm x_{2},\pm x_{3},...,\pm x_{n}$ เราจะสามารถแยกพิจารณากรณีคู่และคี่ไปพร้อมๆ กันได้โดยการแยกตัวประกอบเพื่อให้ทุกพจน์มี degree เป็นคู่เสมอ ดังเช่นตัวอย่าง

$f(x)=8+5x+4x^{2}+2x^{3}=(8+4x^{2})+x(5+2x^{2})\,$

การแยกเช่นนี้เป็นจริงเสมอสำหรับ Polnomial ใดๆ เราจึงแยกเป็น $f(x)=f_{e}(x^{2})+xf_{o}(x^{2})\,$ เมื่อ $f_{e}(x)\,$ เป็นพจน์คู่ของ $f(x)\,$ และ $f_{o}(x)\,$ เป็นพจน์คี่ของ $f(x)\,$ โดยที่เมื่อคำนวณค่าออกมาเพียงครั้งเดียว เราสามารถหาค่าทั้งฝั่งบวกและลบได้ดังสมการ

$f(x_{n})=f_{e}(x_{n}^{2})+xf_{o}(x_{n}^{2})$

$f(-x_{n})=f_{e}(x_{n}^{2})+xf_{o}(x_{n}^{2})$

จากข้างบนทำให้เราสามารถย่อยป้ญหาให้เล็กลงครึ่งหนึ่งได้ แต่ในระบบจำนวนจริงเราไม่สามารถแบ่งปัญหาให้เล็กลงไปกว่าครึ่งได้อีกเพราะการยกกำลังสองในครั้งแรกก็ทำให้เลขทุกตัวกลายเป็นจำนวนบวกไปหมด แต่เราสามารถใช้จำนวนเชิงซ้อนในรูปแบบ Root of Unity เพื่อให้สามารถแบ่งปัญหาลงไปเรื่อยๆ ได้โดยการใช้ Root of Unity มีคุณสมบัติที่น่าสนใจสองประการคือ

• มีคู่ตรงข้ามเสมอ ทำให้สามารถยกกำลังสองเพื่อหาค่าทั้งสองค่าในครั้งเดียวได้
• การยกกำลังสองในแต่ละครั้งจะทำให้ได้ Root of Unity ในอับดับที่ ${\frac {n}{2}}$ เสมอ

การคำนวณค่าของการคูณสมการ Polynomial ใดๆ จึงสามารถทำได้ โดยพิจารณาว่าสมการผลลัพธ์จะมี degree เป็นเท่าใด แล้วเลือกใช้งาน Root of Unity ในลำดับที่สูงกว่านั้นทำให้สามารถคำนวณหาค่าของทุกจุดได้ในเวลาเพียง $n\log {n}\,$

Interpolation

หลังจากที่เราพิจารณาจุดได้มากพอที่จะ Interpolate สมการของผลลัพธ์กลับออกมาได้แล้ว สิ่งที่เราต้องทำต่อไปคือการสร้างสมการที่เป็นผลคูณของสองสมการที่ผ่านมา โดยขณะที่การพิจารณาค่าที่ตำแหน่งต่างๆ ของ $f(x)\,$ นั้นได้ความเร็วเป็น ${\mathcal {O}}(n\log {n})$ แล้วก็ตาม แต่ความเร็วในการ Interpolate สมการกลับขึ้นมาก็ต้องนำมาพิจารณาด้วย

แต่คุณสมบัติของฟังก์ขั่น FFT ที่เราใช้ในการพิจารณาค่าในส่วนที่แล้ว มีคุณสมบัติที่น่าแปลกคือ

จาก $\langle values\rangle =FFT(\langle cofficients\rangle ,\omega )$ เราจะได้ว่า $\langle cofficients\rangle ={\frac {1}{n}}FFT(\langle values\rangle ,\omega ^{-1})$ ซึ่งเนื่องจากสมการในการ Interpolate นั้นเป็นสมการเดียวกับที่ใช้ในการพิจารณาค่าทำให้เราได้ว่าอัลกอลิธึ่มนี้มีความเร็ว ${\mathcal {O}}(n\log {n})$ เสมอ

Proof of Interpolation

การที่เราสามารถพิจารณาค่าจำนวน n จุดของสมการ Polynomial ได้นั้น เราสามารถมองว่าเป็นการคูณกันระหว่าง Matrix ของ Coeffient และ Matrix ของตัวแปร ดังสมการต่อไปนี้

${\begin{bmatrix}f(x_{0})\\f(x_{1})\\\vdots \\f(x_{n-1})\end{bmatrix}}={\begin{bmatrix}1&1&1&\cdots &1\\1&\omega &\omega ^{2}&\cdots &\omega ^{n-1}\\\vdots &\vdots &\vdots &\ddots &\vdots \\1&\omega ^{n-1}&\omega ^{2(n-1)}&\cdots &\omega ^{(n-1)(n-1)}\end{bmatrix}}{\begin{bmatrix}a_{0}\\a_{1}\\\vdots \\a_{n-1}\end{bmatrix}}$

เราให้ Matrix ของ $\omega$ ตรงกลางนั้นชื่อว่า M โดยมันมีรูปแบบที่เรียกว่า Vandermonde Matrix ที่ระบุว่า Matrix ในรูปแบบนี้จะมี Inverse เสมอ

การพิสูจน์สมการการ Interpolate นั้นทำโดยการมอง Matrix M เป็น Matrix ที่ Map เวคเตอร์จาก Space หนึ่งๆ ไปอีก Space หนึ่ง ซึ่งหากทุกแกนของ Space ใหม่นั้นตั้งฉากกันทั้งหมด เราจะสามารถบอกได้ว่าการ Inverse จะทำให้ได้ค่าเดิม คือ Coefficient กลับมาเสมอ และสามารถใช้สูตร

$M_{n}(\omega )^{-1}={\frac {1}{n}}M_{n}(\omega ^{-1})$

ซึ่ง $\omega ^{-1}\,$ ก็ยังคงเป็น Root of Unity อยู่ ทำให้เราสามารถใช้อัลกอลิธึ่มเดิมทำงานได้ต่อไป

ขั้นตอนต่อไปคือการพิสูจน์ว่าแมทริกซ์ M นั้นทุก Column (ซึ่งเป็นเวคเตอร์) ตั้งฉากกันทั้งหมด โดยสามารถทำได้จากการทำ inner product ตามสมการ

$u\cdot v^{*}=u_{0}v_{0}^{*}+u_{1}v_{1}^{*}+\cdots +u_{n-1}v_{n-1}^{*}$ โดยที่ $v^{*}\,$ คือ Conjugate ของ $v\,$

โดยที่การทำ inner product จะให้ผลลัพธ์สูงสุดเมื่อเวคเตอร์ขนานกัน และให้ผลลัพธ์เป็นศูนย์เมื่อเวคเตอร์ตั้งฉากกัน

ในกรณีของ M ที่กล่าวถึงข้างต้น เมื่อเราเลือกคอลัมน์ i และ j ใดๆ มาหามุมระหว่างกันแล้วจะได้ inner product ว่า

$1+\omega ^{i-j}+\omega ^{2(i-j)}+\cdots +\omega ^{(n-1)(i-j)}$

ซึ่งเป็นอนุกรมเลขาคณิตที่มีอัตราส่วนเป็น $\omega ^{(i-j)}$ ทำให้เราได้ผลลัพธ์ของอนุกรมเป็น ${\frac {1-\omega ^{n(i-j)}}{1-\omega ^{i-j}}}$ แต่เนื่องจาก $\omega$ เป็น Root of Unity ทำให้$\omega ^{n}=1$ เสมอ อนุกรมนี้จึงได้ 0 ทั้งหมดนี้เราจึงได้พิสูจน์ว่าเราสามารถใช้อัลกอลิธึ่ม FFT ในการทำ Interpolate สมการกลับมาได้ และทำให้อัลกอลิธึ่มรวมใช้เวลาการทำงานอยู่ใน ${\mathcal {O}}(n\log {n})$

---

แหล่งข้อมูล​อื่น​

อธิบายเรื่อง Big-O-Notation ของ Wiki Pedia

อธิบายเรื่อง Big-O-Notation ของ Wiki Pedia

Inner Product ใช้ในการพิสูจน์เรื่อง Manipulation