ผลต่างระหว่างรุ่นของ "204512/บรรยาย 11"
50653724 (คุย | มีส่วนร่วม) (→ทบทวน) |
50653724 (คุย | มีส่วนร่วม) |
||
| (ไม่แสดง 13 รุ่นระหว่างกลางโดยผู้ใช้คนเดียวกัน) | |||
| แถว 74: | แถว 74: | ||
<br> | <br> | ||
'''วิธีทำ'''<br> | '''วิธีทำ'''<br> | ||
| − | สามารถทำให้ค่า objective = 15 ได้หรือไม่ ?<br> | + | : สามารถทำให้ค่า objective = 15 ได้หรือไม่ ?<br> |
[[ภาพ:Image_example2.jpg|200px]] | [[ภาพ:Image_example2.jpg|200px]] | ||
<pre><nowiki> | <pre><nowiki> | ||
Solution คือ สร้าง Dual ที่มี objective = 15 แล้วสร้าง Primal ที่มี objective = 15 เช่นเดียวกัน | Solution คือ สร้าง Dual ที่มี objective = 15 แล้วสร้าง Primal ที่มี objective = 15 เช่นเดียวกัน | ||
</nowiki></pre> | </nowiki></pre> | ||
| − | + | : กำหนดให้<br><br> | |
[[ภาพ:Image_feasible_infeasible.jpg]]<br><br> | [[ภาพ:Image_feasible_infeasible.jpg]]<br><br> | ||
| + | เราจะทำการปรับค่า Dual(feasible แล้ว) ใหม่ แล้วแก้ Primal(infeasible) เก่า ให้เหมาะสมกับ Dual ใหม่ ทำจนกว่าค่าของ Dual และ Primal(feasible ทั้งคู่) จะมีค่าเท่ากัน<br><br> | ||
[[ภาพ:Image_solution.jpg|750px]] | [[ภาพ:Image_solution.jpg|750px]] | ||
| − | <br> | + | <br> |
{{จบบทพิสูจน์}} | {{จบบทพิสูจน์}} | ||
| แถว 89: | แถว 90: | ||
;นิยาม : | ;นิยาม : | ||
<u>Primal</u> | <u>Primal</u> | ||
| − | :maximize : | + | :maximize : c′x |
:subject to : Ax ≥ b | :subject to : Ax ≥ b | ||
:::: x ≥ 0 | :::: x ≥ 0 | ||
| แถว 138: | แถว 139: | ||
'''วิธีทำ''' | '''วิธีทำ''' | ||
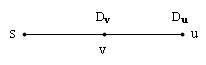
:ให้กราฟ G = (V,E), l(u,v) แทนความยาวเส้นเชื่อม (u,v) | :ให้กราฟ G = (V,E), l(u,v) แทนความยาวเส้นเชื่อม (u,v) | ||
| − | : ตัวแปร D<sub>v</sub> แทนระยะทาง s ไปยัง v | + | : ตัวแปร D<sub>v</sub> แทนระยะทาง s ไปยัง v<br> |
| − | <br> | + | : [[ภาพ:Image_line_distance.jpg]]<br> |
| − | |||
| − | <br> | ||
<u>Primal</u> | <u>Primal</u> | ||
:maximize : | :maximize : | ||
| แถว 162: | แถว 161: | ||
::<math>\sum_{(u,v) \in E} l(u,v) x(u,v) \qquad \longrightarrow </math> <font size='3'>เป็น cost ของ flow</font> | ::<math>\sum_{(u,v) \in E} l(u,v) x(u,v) \qquad \longrightarrow </math> <font size='3'>เป็น cost ของ flow</font> | ||
:subject to : | :subject to : | ||
| − | ::<math>\forall u_{u \in {s,t}} \in V; \qquad \alpha_i + \beta_j \le c_{ij}</math> | + | <!-- ::<math>\forall u_{u \in {s,t}} \in V; \qquad \alpha_i + \beta_j \le c_{ij}</math> |
::<math>\forall i; \qquad \qquad \qquad \qquad \alpha_i \ge 0</math> | ::<math>\forall i; \qquad \qquad \qquad \qquad \alpha_i \ge 0</math> | ||
| − | ::<math>\forall j; \qquad \qquad \qquad \qquad \beta_j \ge 0</math> | + | ::<math>\forall j; \qquad \qquad \qquad \qquad \beta_j \ge 0</math>--> |
| + | |||
| + | ::<math>\sum_{(w,u) \in E} x(w,u) = \sum_{(u,w) \in E} x(u,w)</math> | ||
| + | <br> | ||
| + | :::::[[ภาพ:Image_arrow_in_out.jpg]] | ||
| + | <br> | ||
| + | ::<math>\sum_{(w,u) \in E} x(w,u) = \sum_{(u,w) \in E} x(u,w) \qquad \longrightarrow </math> <font size='3'>flow เข้ามา t 1 หน่วย</font> | ||
| + | ::<math>\sum_{(w,s) \in E} x(w,s) = \sum_{(s,w) \in E} x(s,w) \qquad \longrightarrow </math> <font size='3'>flow ออกจาก s 1 หน่วย</font><br><br> | ||
| + | นี่คือ Dual Program ของ Shortest Path และเป็น form หนึ่งของปัญหา min cost flow | ||
{{จบบทพิสูจน์}} | {{จบบทพิสูจน์}} | ||
| แถว 171: | แถว 178: | ||
:ให้กราฟ G = (V,E) | :ให้กราฟ G = (V,E) | ||
:: capacity u(x,y) บน edge (x,y) | :: capacity u(x,y) บน edge (x,y) | ||
| − | :: cost c(x,y) บน edge (x,y) | + | :: cost c(x,y) บน edge (x,y)<br> |
| + | : [[ภาพ:Image_multi.jpg|140 px]] ที่มี cost = ค่าต่ำสุด (route มากสุด = max flow) | ||
<br> | <br> | ||
| − | + | : <u>min-cost circulation</u> คือ flow = 0 โดยหมุนวนใน flow. จากรูป<br> | |
| − | : | + | :: [[ภาพ:Image_circle.jpg]] |
:minimize : | :minimize : | ||
::<math>\sum_{(u,v) \in E} c(x,y) f(x,y)</math> | ::<math>\sum_{(u,v) \in E} c(x,y) f(x,y)</math> | ||
:subject to : | :subject to : | ||
| − | ::<math>\forall u \in V; \qquad \sum_{(w,x) \in E} f(w,x) = \sum_{(x,w) \in E} f(x,w)</math> | + | ::<math>\forall u \in V; \qquad \sum_{(w,x) \in E} f(w,x) = \sum_{(x,w) \in E} f(x,w)</math> (flow เข้า = flow ออก) |
:::::::::<math>f(x,y) \le u(x,y)</math> | :::::::::<math>f(x,y) \le u(x,y)</math> | ||
---- | ---- | ||
รุ่นแก้ไขปัจจุบันเมื่อ 11:21, 16 กันยายน 2550
จดบันทึกคำบรรยายโดย:
- นางสาว สุกัลยา เลิศวิวัฒน์สกุล รหัส : 50653955
- นางสาว กมลวรรณ โพธิ์แก้ว รหัส : 50653724
เนื้อหา
ทบทวน
Primal Linear Programming
- minimize :
- subject to :
หรือเขียนเป็น matrix form ได้
- minimize : C′x
- subject to : Ax ≥ b ; x เป็นเมตริกซ์ขนาด n-dimension
- x ≥ 0
Dual Linear Programming
- maximize :
- subject to :
หรือเขียนเป็น matrix form ได้
- maximize : y′b
- subject to : ATy ≤ c ; y เป็นเมตริกซ์ขนาด m-dimension
- y ≥ 0
ตัวอย่าง 1 - Assigment
โจทย์ - มีงาน n งาน
- มีพนักงาน n คน
- assign งาน j ให้กับพนักงาน i ใช้ cost Cij
- ต้องการ assign งานให้กับพนักงาน โดยที่งาน 1 งานให้พนักงาน 1 คน
- และพนักงาน 1 คนได้งาน 1 งาน
วิธีทำ
- ให้ xij เป็น 1 ถ้า assign งาน j ให้กับ i
- เป็น 0 ถ้าเป็นอื่นๆ
จากโจทย์เราเขียนเป็นสมการได้ว่า
Primal
- minimize :
- subject to :
จะเห็นว่าสมการข้างบนเป็น integer program ซึ่งต้องใช้เวลาในการแก้นาน ฉะนั้นเราจะทำให้เป็น linear program แทน
ฉะนั้นเราจะแก้ subject to เป็น
- จะได้ว่าเป็น relaxed linear program
เขียนเป็น Dual
- maximize :
- subject to :
เมื่อเราแปลง Primal → Dual ; ค่า Max ของค่าที่นำมาแปลง จะไม่เกินค่า Min ของค่าที่ถูกแปลง
ตัวอย่าง 2
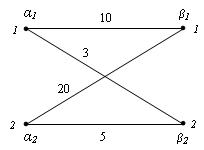
โจทย์ จากตัวอย่างที่ 1 ต้องการหา optimal maching?
วิธีทำ
- สามารถทำให้ค่า objective = 15 ได้หรือไม่ ?
Solution คือ สร้าง Dual ที่มี objective = 15 แล้วสร้าง Primal ที่มี objective = 15 เช่นเดียวกัน
- กำหนดให้
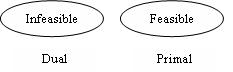
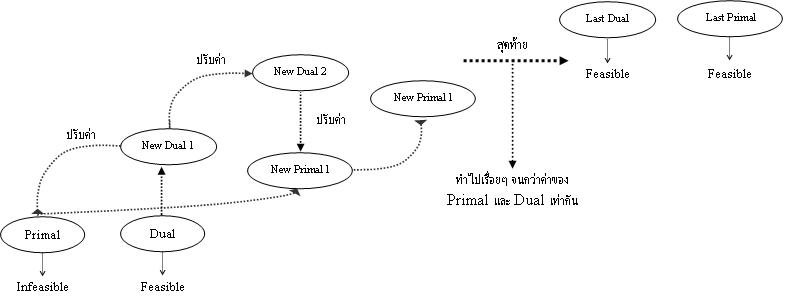
เราจะทำการปรับค่า Dual(feasible แล้ว) ใหม่ แล้วแก้ Primal(infeasible) เก่า ให้เหมาะสมกับ Dual ใหม่ ทำจนกว่าค่าของ Dual และ Primal(feasible ทั้งคู่) จะมีค่าเท่ากัน
Duality
จาก Prob. priallity
- นิยาม
Primal
- maximize : c′x
- subject to : Ax ≥ b
- x ≥ 0
Dual
- maximize : y′b
- subject to : ATy ≤ c
- y ≥ 0
Weak duality
Thm:
- ถ้า x และ y เป็น feasible solution
- y′b ≤ c′x
Proof:
- y′b ≤ y′Ax ≤ c′x
Storng duality
Thm:
- ถ้า x* และ y* เป็น 2optimal solution ของ PLP, DLP
- c′x* = b′y*
Complementary Slackness
Dual:
- maximize : y′b
- ATy + s = c ; s เป็น matrix ขนาด n มิติเท่า y
- y ≥ 0
- s ≥ 0
Proof:
- (ATy*′ + s)x* = y*′b
- y*′Ax + sx* = y*′b
- y*′b + sx*′ = y*′b
- sx* = 0
ตัวอย่าง 3 : Shortest path
โจทย์ หา shortest path จาก s
วิธีทำPrimal
- maximize :
- Dt - Ds
- subject to :
จะเห็นว่าสมการข้างบนดูยาก เราจะเขียนใหม่ได้
- maximize :
- Dt - Ds
- subject to :
เขียนเป็น Dual ได้
- minimize :
- เป็น cost ของ flow
- subject to :
- flow เข้ามา t 1 หน่วย
- flow ออกจาก s 1 หน่วย
นี่คือ Dual Program ของ Shortest Path และเป็น form หนึ่งของปัญหา min cost flow
Min-cost Maximun flow
- min-cost flow คือการหา flow ที่มี cost ต่ำที่สุด
- ให้กราฟ G = (V,E)
- capacity u(x,y) บน edge (x,y)
- cost c(x,y) บน edge (x,y)
 ที่มี cost = ค่าต่ำสุด (route มากสุด = max flow)
ที่มี cost = ค่าต่ำสุด (route มากสุด = max flow)
- min-cost circulation คือ flow = 0 โดยหมุนวนใน flow. จากรูป
- minimize :
- subject to :
- (flow เข้า = flow ออก)
- (flow เข้า = flow ออก)