ผลต่างระหว่างรุ่นของ "204512/บรรยาย 8"
Top (คุย | มีส่วนร่วม) |
|||
| (ไม่แสดง 47 รุ่นระหว่างกลางโดยผู้ใช้ 4 คน) | |||
| แถว 1: | แถว 1: | ||
{{หัวคำบรรยาย|204512}} | {{หัวคำบรรยาย|204512}} | ||
| + | '''จดบันทึกคำบรรยายโดย:''' วัชรพัฐ เมตตานันท <font color="red"></font> | ||
| − | การบรรยายครั้งนี้จะกล่าวถึงการแก้ปัญหา network flows โดยใช้แนวคิดเกี่ยวกับ blocking flows ซึ่งนำไปสู่อัลกอริทึมของ Dinic | + | การบรรยายครั้งนี้จะกล่าวถึงการแก้ปัญหา network flows โดยใช้แนวคิดเกี่ยวกับ blocking flows ซึ่งนำไปสู่อัลกอริทึมของ E.A.Dinic |
==Blocking Flows== | ==Blocking Flows== | ||
| แถว 18: | แถว 19: | ||
<center> | <center> | ||
| − | [[ภาพ:fig8.jpg]] | + | [[ภาพ:fig8-1.jpg]] |
รูปที่ 8.1 ตัวอย่าง blocking flow | รูปที่ 8.1 ตัวอย่าง blocking flow | ||
| แถว 25: | แถว 26: | ||
==Level Graphs== | ==Level Graphs== | ||
| + | ในอัลกอริทึมของ Dinic จะมีขั้นตอนการหา blocking flow บนกราฟที่มีลักษณะพิเศษบางอย่าง ซึ่งเรียกว่า level graph แต่ก่อนจะนิยาม level graph ได้เราต้องให้นิยาม level ของแต่ละโหนดในกราฟก่อน | ||
| + | {{กล่องนิยาม| | ||
| + | ;นิยาม 8.3 : ให้ต้นทาง ''s'', สำหรับโหนด ''v'' ใดๆในกราฟ ''l(v)'' คือระยะทางที่สั้นที่สุดจาก ''s'' ไปยัง ''v'' โดยระยะทางบน path ''p'' หมายถึงจำนวน edge บน path ''p''}} | ||
| + | ต่อมาเราจะสามารถนิยาม level graph ได้ดังนี้ | ||
| + | {{กล่องนิยาม| | ||
| + | ;นิยาม 8.4 : '''level graph''' ของกราฟ ''G'' คือสับกราฟของ ''G'' ที่มีเฉพาะ edge (''u'',''v'') ที่ | ||
| + | |||
| + | <center><math>l(v)=l(u)+1\,</math></center>}} | ||
| + | ;ตัวอย่าง 8.2 : | ||
| + | |||
| + | <center> | ||
| + | [[ภาพ:fig8-2.jpg]] | ||
| + | |||
| + | รูปที่ 8.2 ตัวอย่าง level graph | ||
| + | </center> | ||
| + | |||
| + | พิจารณากราฟ ''G'' ในรูปที่ 8.2 โดย edge ทุกเส้นในรูปอยู่ใน ''G'' level graph ของ ''G'' จะเป็นกราฟที่มีเฉพาะ edge ที่เป็นเส้นทึบในรูป ค่า level ของแต่ละโหนดถูกแสดงด้วยตัวเลขสีแดง | ||
==Dinic's Blocking Flow Algorithm== | ==Dinic's Blocking Flow Algorithm== | ||
| + | ===Blocking Step=== | ||
| + | [[ภาพ:Y-Dinitz.jpg|thumb|150px|right|[http://www.cs.bgu.ac.il/~dinitz/ Yefim Dinitz] ภาพจาก http://www.cs.bgu.ac.il/~dinitz/]] | ||
| + | |||
| + | อัลกอริทึมสำหรับหา maximum flow ของ Dinic ประกอบด้วยการตั้งค่าเริ่มต้นให้ flow เป็นศูนย์ และทำขั้นตอน blocking step ซ้ำไปเรื่อยๆจนโหนด ''t'' ไม่อยู่ใน level graph (ดูรูปที่ 8.3) โดยขั้นตอน blocking step จะแสดงต่อไปนี้ | ||
| + | <center> | ||
| + | [[ภาพ:Fig8-3.jpg]] | ||
| + | |||
| + | รูปที่่่่่ 8.3 อัลกอริทึมสำหรับหา maximum flow ของ Dinic (''a'') กราฟนำเข้า(input graph) (''b'') level graph และ blocking flow แรก levelของแต่ละโหนดแสดงอยู่ในวงเล็บ (''c'') level graph และ blocking flow ที่สอง (''d'') level graph และ blocking flow ที่สาม (''e'') flow สุดท้าย จะได้ minimum cut เป็น ({s,a,b,d},{c,t}) | ||
| + | </center> | ||
| + | BLOCKING STEP(Dinic) : | ||
| + | |||
| + | ให้ <math>f\,</math> เป็น flow ปัจจุบัน และ <math>G_f\,</math> เป็น residual graph | ||
| + | 1 หา level graph <math>L\,</math> ของ <math>G_f\,</math> | ||
| + | 2 หา blocking flow <math>f'\,</math> ใน <math>L\,</math> | ||
| + | 3 ปรับ <math>f\,</math> ให้เป็น <math>f+f'\,</math> | ||
| + | |||
| + | ===Running Time=== | ||
| + | จากตัวอย่างจะเห็นว่า ใน residual graph ของ flow สุดท้ายจะไม่มี path จาก ''s'' ไปยัง ''t'' เหลืออยู่อีก ดังนั้นอัลกอริทึมของ Dinic ให้ผลลัพธ์เป็น maximum flow | ||
| + | ต่อไปจะเป็นการพิสูจน์เวลาทำงานของอัลกอริทึม ให้กราฟนำเข้ามีจำนวนโหนดเท่ากับ ''n'' และจำนวน edge เท่ากับ ''m'' เราจะเริ่มจากทฤษฎีบทย่อยต่อไปนี้ | ||
| + | |||
| + | {{thm-box|;Lemma 8.5 : สำหรับการทำ blocking step ครั้งใดๆ ให้ <math>l(v)\,</math> และ <math>l'(v)\,</math> แทน level ของโหนด <math>v\,</math> ใน level graph ก่อนและหลังการทำ blocking step ตามลำดับ จะได้ว่า | ||
| + | |||
| + | <center><math>l'(t)>l(t)\,</math></center>}} | ||
| + | |||
| + | {{begin-pf}} | ||
| + | ''Proof'': พิจารณา blocking step, ให้ <math>f\,</math> แทน flow ปัจจุบัน, <math>R\,</math> แทน residual graph ของ <math>f\,</math>, <math>L\,</math> แทน level graph, และ <math>R'\,</math> เป็น residual graph หลังการทำ blocking step พิจารณาแต่ละ edge <math>(v,w)\,</math> ใน<math>R\,</math> จะมี <math>l(w) \le l(v)+1</math> แต่ละ edge ใน <math>R'\,</math> จะมาจาก edge ใน <math>R\,</math> หรือไม่ก็เป็น reverse ของ edge ใน <math>L\,</math> ดังนั้น แต่ละ edge <math>(v,w)\,</math> ใน <math>R'\,</math> จะมี <math>l(w) \le l(v)+1\,</math> แสดงว่า <math>l'(t) \ge l(t)\,</math> | ||
| + | |||
| + | สมมติให้ <math>l'(t)=l(t)\,</math> ให้ <math>p\,</math> เป็น shortest path ใดๆ จาก <math>s\,</math> ไปยัง <math>t\,</math> ใน <math>R\,</math> จะได้ว่า <math>l(w)=l(v)+1\,</math> สำหรับทุกๆ edge <math>(v,w)\,</math> ใน <math>p\,</math> ซึ่งแสดงว่าทุกๆ edge ดังกล่าวอยู่ใน <math>L\,</math> เกิดข้อขัดแย้งว่า edge ดังกล่าวอย่างน้อยหนึ่ง edge จะต้อง saturated จาก blocking flow ที่พบบน <math>L\,</math> และไม่ปรากฏบน <math>R'\,</math> ดังนั้นจึงสรุปได้ว่า <math>l'(t)>l(t)\,</math> | ||
| + | {{end-pf}} | ||
| + | |||
| + | จากทฤษฎีบทย่อยข้างต้น สามารถสรุปได้ดังนี้ | ||
| + | {{thm-box|;Theorem 8.6 : การหา maximum flow โดยใช้อัลกอริทึมของ Dinic จะทำ blocking step ไม่เกิน ''n''-1 รอบ}} | ||
| + | {{begin-pf}} | ||
| + | ''Proof'': จาก Lemma 8.5 จะได้ว่า level ของโหนด ''t'' จะเพิ่มขึ้นหรือกลายเป็น undefined ทุกครั้งหลังการทำ blocking step ซึ่ง level ของโหนด ''t'' มีค่าได้น้อยสุดเป็น 1 และมากสุดเป็น ''n''-1 ดังนั้น จึงเกิดการทำ blocking step ได้ไม่เกิน ''n''-1 ครั้ง | ||
| + | {{end-pf}} | ||
| + | |||
| + | สำหรับการหา blocking flow ในแต่ละครั้ง สามารถทำได้ในเวลา <math>O(nm)\,</math> ดังนั้นจึงได้เวลาการทำงานสำหรับอัลกอริทึมของ Dinic ดังทฤษฎีบทต่อไปนี้ | ||
| + | {{thm-box|;Theorem 8.7 : อัลกอริทึมสำหรับหา maximum flow ของ Dinic ใช้เวลาทำงาน | ||
| + | |||
| + | <center><math>O(n^2m)\,</math></center>}} | ||
| + | |||
| + | ===Unit Network=== | ||
| + | |||
| + | ในกราฟที่มีลักษณะพิเศษบางกรณี อัลกอริทึมของ Dinic สามารถทำงานได้มีประสิทธิภาพมากกว่าใน Theorem 8.7 (ใช้จำนวนรอบดีกว่า Theorem 8.6) เช่นใน unit network ซึ่งทุกๆ edge จะมีความจุเป็นจำนวนเต็ม โดย แต่ละ node <math>v</math> ที่ไม่ใช่ <math>s</math> หรือ <math>t</math> <math>v</math> จะต้องเป็นหนึ่งในสองกรณีต่อไปนี้ | ||
| + | #มี edge ชี้เข้าเพียง edge เดียว โดยมีความจุเท่ากับ 1 หรือ | ||
| + | #มี edge ชี้ออกเพียง edge เดียว โดยมีความจุเท่ากับ 1 | ||
| + | |||
| + | {{thm-box|;Theorem 8.8 : สำหรับ unit network อัลกอริทึมของ Dinic จะทำ blocking step ไม่เกิน <math>O(\sqrt n)</math> ครั้ง}} | ||
| + | |||
| + | {{begin-pf}} | ||
| + | ''Proof'': พิจารณา blocking step ให้ <math>f\,</math> เป็น flow ปัจจุบัน, <math>f^*\,</math> เป็น maximum flow, และ <math>R\,</math> เป็น residual graph ของ <math>f\,</math> ดังนั้น <math>f^*-f\,</math> จะต้องเป็น flow บน <math>R\,</math> | ||
| + | |||
| + | เนื่องจาก <math>f\,</math> เป็นจำนวนเต็ม, <math>R\,</math> เป็น unit network, <math>f^*-f\,</math> จะต้องเป็น 0 หรือ 1 บนทุกๆ edge ดังนั้น เราสามารถแบ่ง edge ที่ <math>f^*-f\,</math> เป็น 1 ให้เป็นกลุ่มของ path จาก <math>s</math> ไปยัง <math>t</math> จำนวน <math>|f^*|-|f|\,</math> path (อาจมี cycle) | ||
| + | |||
| + | เนื่องจาก <math>R\,</math> เป็น unit แต่ละ node ที่ไม่ใช่ <math>s</math> หรือ <math>t</math> จะอยู่บน path ได้ไม่เกิน 1 path ซึ่งแสดงว่า <math>f\,</math> จะมี augmenting path ที่มีความยาวไม่เกิน <math>(n-2)/(|f^*|-|f|)+1\,</math> | ||
| + | |||
| + | หลังจาก <math>\lceil\sqrt{n-2}\rceil</math> blocking step, augmenting path ที่สั้นที่สุดจะประกอบด้วย edge อย่างน้อย <math>\sqrt{n-2}+1</math> edge (จาก Theorem 8.6) ดังนั้น <math>\sqrt{n-2}+1 \le (n-1)/(|f^*|-|f|)+1\,</math> โดยที่ <math>|f^*|-|f| \le \sqrt{n-2}</math> จึงสรุปได้ว่า หลังจาก <math>\lfloor \sqrt{n-2} \rfloor</math> blocking step flow ที่ได้จะเป็น max flow | ||
| + | {{end-pf}} | ||
รุ่นแก้ไขปัจจุบันเมื่อ 11:08, 8 ตุลาคม 2550
บันทึกคำบรรยายวิชา 204512 นี้ เป็นบันทึกที่นิสิตเขียนขึ้น เนื้อหาโดยมากยังไม่ผ่านการตรวจสอบอย่างละเอียด การนำไปใช้ควรระมัดระวัง
จดบันทึกคำบรรยายโดย: วัชรพัฐ เมตตานันท
การบรรยายครั้งนี้จะกล่าวถึงการแก้ปัญหา network flows โดยใช้แนวคิดเกี่ยวกับ blocking flows ซึ่งนำไปสู่อัลกอริทึมของ E.A.Dinic
เนื้อหา
Blocking Flows
สำหรับการนิยาม blocking flows เราจะต้องให้นิยาม saturated edge ก่อน
- นิยาม 8.1
- ให้ network G และ flow f จะกล่าวว่า edge e saturated (อิ่มตัว) ถ้า f ใช้ capacity ของ e จนหมด นั่นคือ
และเราสามารถนิยาม blocking flows ได้ดังนี้
- นิยาม 8.2
- เราจะเรียก flow f ว่าเป็น blocking flow ถ้า ทุกๆ s-t path มี saturated edge อย่างน้อยหนึ่ง edge
จะเห็นว่าถ้า f เป็น blocking flow แล้ว เราไม่สามารถเพิ่มขนาดของ flow โดยการดัน flow เพิ่มตาม path ใน G ได้อีก เนื่องจากทุก path มี saturated edge อยู่ แต่เราอาจเพิ่มขนาดของ flow ได้โดยการลด flow บน edge บางเส้น และเพิ่มไปยัง edge อื่น พิจารณาตัวอย่างต่อไปนี้
- ตัวอย่าง 8.1
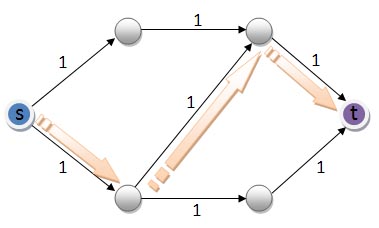
- ให้กราฟมีทิศทางดังรูปที่ 8.1 โดย edge ทุกๆเส้นมี capacity เท่ากับ 1
รูปที่ 8.1 ตัวอย่าง blocking flow
พิจารณา flow f ที่มีขนาดเท่ากับ 1 ตามลูกศรสีส้มในรูป จะเห็นว่า edge ทั้งสามเส้นที่มี flow f ไหลผ่าน เป็น saturated edge ทั้งสิ้น และทุกๆ path จาก s ไปยัง t จะมี saturated edge อย่างน้อยหนึ่งเส้น ซึ่งทำให้เราไม่สามารถเพิ่ม flow ตาม path เหล่านี้ได้อีก ดังนั้น f ในตัวอย่างนี้เป็น blocking flow
Level Graphs
ในอัลกอริทึมของ Dinic จะมีขั้นตอนการหา blocking flow บนกราฟที่มีลักษณะพิเศษบางอย่าง ซึ่งเรียกว่า level graph แต่ก่อนจะนิยาม level graph ได้เราต้องให้นิยาม level ของแต่ละโหนดในกราฟก่อน
- นิยาม 8.3
- ให้ต้นทาง s, สำหรับโหนด v ใดๆในกราฟ l(v) คือระยะทางที่สั้นที่สุดจาก s ไปยัง v โดยระยะทางบน path p หมายถึงจำนวน edge บน path p
ต่อมาเราจะสามารถนิยาม level graph ได้ดังนี้
- นิยาม 8.4
- level graph ของกราฟ G คือสับกราฟของ G ที่มีเฉพาะ edge (u,v) ที่
- ตัวอย่าง 8.2
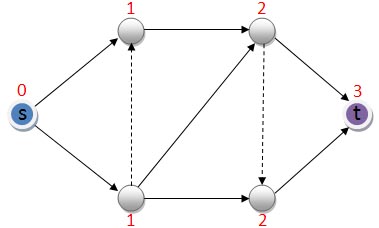
รูปที่ 8.2 ตัวอย่าง level graph
พิจารณากราฟ G ในรูปที่ 8.2 โดย edge ทุกเส้นในรูปอยู่ใน G level graph ของ G จะเป็นกราฟที่มีเฉพาะ edge ที่เป็นเส้นทึบในรูป ค่า level ของแต่ละโหนดถูกแสดงด้วยตัวเลขสีแดง
Dinic's Blocking Flow Algorithm
Blocking Step
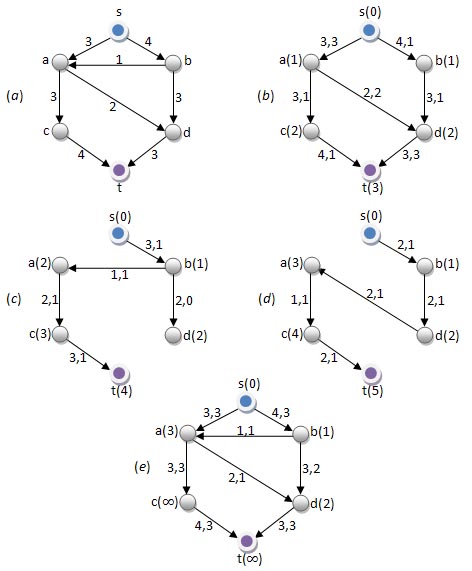
อัลกอริทึมสำหรับหา maximum flow ของ Dinic ประกอบด้วยการตั้งค่าเริ่มต้นให้ flow เป็นศูนย์ และทำขั้นตอน blocking step ซ้ำไปเรื่อยๆจนโหนด t ไม่อยู่ใน level graph (ดูรูปที่ 8.3) โดยขั้นตอน blocking step จะแสดงต่อไปนี้
รูปที่่่่่ 8.3 อัลกอริทึมสำหรับหา maximum flow ของ Dinic (a) กราฟนำเข้า(input graph) (b) level graph และ blocking flow แรก levelของแต่ละโหนดแสดงอยู่ในวงเล็บ (c) level graph และ blocking flow ที่สอง (d) level graph และ blocking flow ที่สาม (e) flow สุดท้าย จะได้ minimum cut เป็น ({s,a,b,d},{c,t})
BLOCKING STEP(Dinic) : ให้ เป็น flow ปัจจุบัน และ เป็น residual graph 1 หา level graph ของ 2 หา blocking flow ใน 3 ปรับ ให้เป็น
Running Time
จากตัวอย่างจะเห็นว่า ใน residual graph ของ flow สุดท้ายจะไม่มี path จาก s ไปยัง t เหลืออยู่อีก ดังนั้นอัลกอริทึมของ Dinic ให้ผลลัพธ์เป็น maximum flow ต่อไปจะเป็นการพิสูจน์เวลาทำงานของอัลกอริทึม ให้กราฟนำเข้ามีจำนวนโหนดเท่ากับ n และจำนวน edge เท่ากับ m เราจะเริ่มจากทฤษฎีบทย่อยต่อไปนี้
- Lemma 8.5
- สำหรับการทำ blocking step ครั้งใดๆ ให้ และ แทน level ของโหนด ใน level graph ก่อนและหลังการทำ blocking step ตามลำดับ จะได้ว่า
Proof: พิจารณา blocking step, ให้ แทน flow ปัจจุบัน, แทน residual graph ของ , แทน level graph, และ เป็น residual graph หลังการทำ blocking step พิจารณาแต่ละ edge ใน จะมี แต่ละ edge ใน จะมาจาก edge ใน หรือไม่ก็เป็น reverse ของ edge ใน ดังนั้น แต่ละ edge ใน จะมี แสดงว่า
สมมติให้ ให้ เป็น shortest path ใดๆ จาก ไปยัง ใน จะได้ว่า สำหรับทุกๆ edge ใน ซึ่งแสดงว่าทุกๆ edge ดังกล่าวอยู่ใน เกิดข้อขัดแย้งว่า edge ดังกล่าวอย่างน้อยหนึ่ง edge จะต้อง saturated จาก blocking flow ที่พบบน และไม่ปรากฏบน ดังนั้นจึงสรุปได้ว่า
จากทฤษฎีบทย่อยข้างต้น สามารถสรุปได้ดังนี้
- Theorem 8.6
- การหา maximum flow โดยใช้อัลกอริทึมของ Dinic จะทำ blocking step ไม่เกิน n-1 รอบ
Proof: จาก Lemma 8.5 จะได้ว่า level ของโหนด t จะเพิ่มขึ้นหรือกลายเป็น undefined ทุกครั้งหลังการทำ blocking step ซึ่ง level ของโหนด t มีค่าได้น้อยสุดเป็น 1 และมากสุดเป็น n-1 ดังนั้น จึงเกิดการทำ blocking step ได้ไม่เกิน n-1 ครั้ง
สำหรับการหา blocking flow ในแต่ละครั้ง สามารถทำได้ในเวลา ดังนั้นจึงได้เวลาการทำงานสำหรับอัลกอริทึมของ Dinic ดังทฤษฎีบทต่อไปนี้
- Theorem 8.7
- อัลกอริทึมสำหรับหา maximum flow ของ Dinic ใช้เวลาทำงาน
Unit Network
ในกราฟที่มีลักษณะพิเศษบางกรณี อัลกอริทึมของ Dinic สามารถทำงานได้มีประสิทธิภาพมากกว่าใน Theorem 8.7 (ใช้จำนวนรอบดีกว่า Theorem 8.6) เช่นใน unit network ซึ่งทุกๆ edge จะมีความจุเป็นจำนวนเต็ม โดย แต่ละ node ที่ไม่ใช่ หรือ จะต้องเป็นหนึ่งในสองกรณีต่อไปนี้
- มี edge ชี้เข้าเพียง edge เดียว โดยมีความจุเท่ากับ 1 หรือ
- มี edge ชี้ออกเพียง edge เดียว โดยมีความจุเท่ากับ 1
- Theorem 8.8
- สำหรับ unit network อัลกอริทึมของ Dinic จะทำ blocking step ไม่เกิน ครั้ง
Proof: พิจารณา blocking step ให้ เป็น flow ปัจจุบัน, เป็น maximum flow, และ เป็น residual graph ของ ดังนั้น จะต้องเป็น flow บน
เนื่องจาก เป็นจำนวนเต็ม, เป็น unit network, จะต้องเป็น 0 หรือ 1 บนทุกๆ edge ดังนั้น เราสามารถแบ่ง edge ที่ เป็น 1 ให้เป็นกลุ่มของ path จาก ไปยัง จำนวน path (อาจมี cycle)
เนื่องจาก เป็น unit แต่ละ node ที่ไม่ใช่ หรือ จะอยู่บน path ได้ไม่เกิน 1 path ซึ่งแสดงว่า จะมี augmenting path ที่มีความยาวไม่เกิน
หลังจาก blocking step, augmenting path ที่สั้นที่สุดจะประกอบด้วย edge อย่างน้อย edge (จาก Theorem 8.6) ดังนั้น โดยที่ จึงสรุปได้ว่า หลังจาก blocking step flow ที่ได้จะเป็น max flow