ผลต่างระหว่างรุ่นของ "01204512/congestion1"
Jittat (คุย | มีส่วนร่วม) |
Jittat (คุย | มีส่วนร่วม) ล (ย้อนการแก้ไขของ CarolAnderson (Talk) ไปยังรุ่นของ Jittat) |
||
| (ไม่แสดง 17 รุ่นระหว่างกลางโดยผู้ใช้ 2 คน) | |||
| แถว 1: | แถว 1: | ||
| − | : หน้านี้เป็นเอกสารประกอบวิชา [[01204512]] | + | : หน้านี้เป็นเอกสารประกอบวิชา [[01204512]] เนื้อหาจาก [http://www.cs.berkeley.edu/~satishr/cs270/sp12/ http://www.cs.berkeley.edu/~satishr/cs270/sp12/] lecture 1 |
| − | |||
| − | : | ||
== ปัญหา congestion minimization == | == ปัญหา congestion minimization == | ||
| แถว 36: | แถว 34: | ||
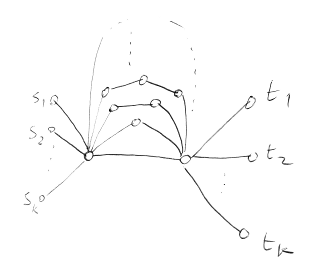
ถ้าเราพิจารณาให้ดี เราจะพบว่า มีตัวอย่างง่าย ๆ ที่ผลลัพธ์ที่ได้ มี congestion เท่ากับ <math>k</math> ในขณะที่คำตอบที่ดีที่สุดให้ congestion แค่ 1 เท่านั้น | ถ้าเราพิจารณาให้ดี เราจะพบว่า มีตัวอย่างง่าย ๆ ที่ผลลัพธ์ที่ได้ มี congestion เท่ากับ <math>k</math> ในขณะที่คำตอบที่ดีที่สุดให้ congestion แค่ 1 เท่านั้น | ||
| − | + | [[Image:Cong-512.png]] | |
สังเกตว่าทุก ๆ path จะพยายามไปใช้เส้นทางที่สั้นที่สุดพร้อม ๆ กันหมด เราจะพยายามแก้ปัญหานี้โดยการทำให้เส้นทางที่สั้นที่สุดมีความ "น่าใช้" ลดลงเรื่อย ๆ เราจะทดลองหลาย ๆ แบบ | สังเกตว่าทุก ๆ path จะพยายามไปใช้เส้นทางที่สั้นที่สุดพร้อม ๆ กันหมด เราจะพยายามแก้ปัญหานี้โดยการทำให้เส้นทางที่สั้นที่สุดมีความ "น่าใช้" ลดลงเรื่อย ๆ เราจะทดลองหลาย ๆ แบบ | ||
=== การปรับระยะทางแบบเชิงเส้น === | === การปรับระยะทางแบบเชิงเส้น === | ||
| − | เราจะปรับความยาวของ edge ตาม congestion ของ edge นั้น กล่าวคือ ในแต่ละรอบที่เราหาเส้นทางที่สั้นที่สุดเราจะให้ <math>\ell(e)=c(e)</math> สำหรับทุก ๆ เส้นเชื่อม | + | เราจะปรับความยาวของ edge ตาม congestion ของ edge นั้น กล่าวคือ ในแต่ละรอบที่เราหาเส้นทางที่สั้นที่สุดเราจะให้ <math>\ell(e)=c(e)</math> สำหรับทุก ๆ เส้นเชื่อม เราจะทยอยเพิ่ม path เข้าไปในระบบจนกว่าระบบจะ "นิ่ง" |
| + | |||
| + | เมื่อใดที่เราจะเรียกว่าระบบ "นิ่ง"? ถ้าเราเลือกเส้นทางใด เราจะเพิ่มค่า congestion ให้กับ edge บน เส้นทางนั้น ทำให้ในรอบต่อไปเวลาเราจะเลือกเส้นทางที่สั้นที่สุด เราจะเลือกได้เส้นทางอื่น ในที่นี้เราจะพิจารณาแบบง่ายไปก่อนว่า เราจะเรียกว่าระบบนิ่ง เมื่อความยาวของ path ใด ๆ เท่ากัน | ||
| + | |||
| + | สังเกตว่าในกรณีนี้ ความยาวของ edge ใน path ที่มี edge เดียว (เส้นล่างสุด) จะต้องยาวเท่ากับเส้นอื่น ๆ ทั้ง <math>k</math> เส้น นั่นคือเราจะได้ว่า | ||
| + | |||
| + | <math> | ||
| + | c(e_1)=2\cdot c(e_2)=3\cdot c(e_3)=\cdots = k\cdot c(e_k) | ||
| + | </math> | ||
| + | |||
| + | เมื่อ <math>e_i</math> คือ edge แรกใน path ที่มีจำนวน edge เท่ากับ <math>i</math> edges (สังเกตว่าทุก ๆ edge ใน path เดี่ยวกัน จะต้องมี congestion เท่ากัน) | ||
| + | |||
| + | สังเกตว่า ผลลัพธ์ที่เราได้ จะต้องเป็น flow ที่มีขนาด k หน่วย จากจุดสมดุลย์ข้างต้น เราส่ง flow ไปแล้วทั้งสิ้นเท่ากับ | ||
| + | |||
| + | <math>c(e_1)+c(e_2)+\cdots+c(e_k)</math> หน่วย ดังนั้นเราจะ scale flow ดังกล่าวลง เพื่อให้ได้ผลรวมเท่ากับ <math>k</math> เราจะต้องหาตัวคูณ <math>\alpha</math> ที่สอดคล้องกับ | ||
| + | |||
| + | <math>\alpha\cdot(c(e_1)+c(e_2)+\cdots+c(e_k))=k</math> นั่นคือ <math>\alpha=\frac{k}{c(e_1)+c(e_2)+\cdots+c(e_k)}</math> | ||
| + | |||
| + | จัดนิพจน์ใหม่ ตามสมการด้านบน โดยแทนค่า <math>c(e_i)=c(e_1)/i</math> เราจะได้ว่า | ||
| + | |||
| + | <math> | ||
| + | \alpha = \frac{k}{c(e_1)+\frac{c(e_1)}{2}+\frac{c(e_1)}{3}+\cdots+\frac{c(e_1)}{k}} | ||
| + | = \frac{k}{c(e_1)\left(1+\frac{1}{2}+\frac{1}{3}+\cdots+\frac{1}{k}\right)} | ||
| + | </math> | ||
| + | |||
| + | สังเกตว่าจำนวน flow ทั้งหมดที่ผ่านเส้นเชื่อม <math>e_1</math> หลังจากการ scale ด้วย <math>\alpha</math> แล้ว จะมีค่าเท่ากับ | ||
| + | |||
| + | <math> | ||
| + | \alpha\cdot c(e_1) = \frac{k}{1+\frac{1}{2}+\frac{1}{3}+\cdots+\frac{1}{k}}\approx k/{\ln k} | ||
| + | </math> | ||
| + | |||
| + | ซึ่งดีกว่าค่า congestion <math>k</math> ในตอนแรก | ||
| + | |||
| + | === การปรับระยะทางเป็นกำลังสอง === | ||
| + | แทนที่เราจะปรับแบบเชิงเส้น เราจะปรับความยาวให้มากขึ้น โดยเราจะให้ <math>\ell(e)=c(e)^2</math> สำหรับทุก ๆ เส้นเชื่อม | ||
| + | |||
| + | ในกรณีนี้ เราจะได้ว่า เส้นทางทุกเส้นจะมีความยาวเท่ากันก็ต่อเมื่อ | ||
| + | |||
| + | <math> | ||
| + | c(e_1)^2=2\cdot c(e_2)^2=3\cdot c(e_3)^2=\cdots = k\cdot c(e_k)^2 | ||
| + | </math> | ||
| + | |||
| + | หรือ <math>c(e_i) = \sqrt{c(e_1)^2/i} = c(e_1)/\sqrt{i}</math> | ||
| + | |||
| + | เราแทนค่านี้ลงไปใหม่ ในการวิเคราะห์เดิมในกรณีที่ปรับค่าความยาวเป็นเชิงเสิ้น เราจะได้ว่า | ||
| + | |||
| + | <math> | ||
| + | \alpha = \frac{k}{c(e_1)+\frac{c(e_1)}{\sqrt{2}}+\frac{c(e_1)}{\sqrt{3}}+\cdots+\frac{c(e_1)}{\sqrt{k}}} | ||
| + | = \frac{k}{c(e_1)\left(1+\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{3}}+\cdots+\frac{1}{\sqrt{k}}\right)} | ||
| + | </math> | ||
| + | |||
| + | ดังนั้นจำนวน flow ทั้งหมดผ่านเส้นเชื่อม <math>e_1</math> หลังจากการ scale ด้วย <math>\alpha</math> แล้ว จะมีค่าเท่ากับ | ||
| + | |||
| + | <math> | ||
| + | c(e_1)\cdot\frac{k}{c(e_1)\left(1+\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{3}}+\cdots+\frac{1}{\sqrt{k}}\right)}= | ||
| + | \frac{k}{1+\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{3}}+\cdots+\frac{1}{\sqrt{k}}} | ||
| + | </math> | ||
| + | |||
| + | สังเกตว่า <math>\frac{1}{\sqrt{i}}\geq \frac{1}{\sqrt{k}}</math> เมื่อ <math>1\leq i \leq k</math> ดังนั้น | ||
| + | |||
| + | <math>\frac{1}{1}+\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{3}}+\cdots+\frac{1}{\sqrt{k}}\geq | ||
| + | k\cdot\frac{1}{\sqrt{k}}= | ||
| + | \sqrt{k}</math> | ||
| + | |||
| + | ดังนั้น ค่า congestion บน <math>e_1</math> หลักการ scale จะมีค่าไม่เกิน <math> k/\sqrt{k} = \sqrt{k}</math> | ||
| + | |||
| + | === การปรับระยะทางแบบยกกำลัง === | ||
| + | ถ้าเราจะปรับความยาวให้มากขึ้น โดยให้ <math>\ell(e)=2^{c(e)}</math> สำหรับทุก ๆ เส้นเชื่อม | ||
| + | |||
| + | ในกรณีนี้ เราจะได้ว่า เส้นทางทุกเส้นจะมีความยาวเท่ากันก็ต่อเมื่อ | ||
| + | |||
| + | <math> | ||
| + | 2^{c(e_1)}=2\cdot 2^{c(e_2)}=3\cdot 2^{c(e_3)}=\cdots = k\cdot 2^{c(e_k)} | ||
| + | </math> | ||
| + | |||
| + | หรือ <math>c(e_i) = \log 2^{c(e_1)}/i = c(e_1)-\log i</math> เมื่อนำสมการนี้เข้าไปแทนในการวิเคราะห์เราสามารถแสดงได้ไม่ยากว่า congestion ที่มากที่สุด จะมีค่าไม่เกิน <math>O(\log k)</math> | ||
รุ่นแก้ไขปัจจุบันเมื่อ 06:03, 5 สิงหาคม 2555
- หน้านี้เป็นเอกสารประกอบวิชา 01204512 เนื้อหาจาก http://www.cs.berkeley.edu/~satishr/cs270/sp12/ lecture 1
เนื้อหา
ปัญหา congestion minimization
ให้กราฟ และเซตของคู่ของจุดยอด จำนวน คู่ เราต้องการหาเซตของเส้นทาง (path) ที่เชื่อมจุดยอดแต่ละคู่ โดยต้องการทำให้จำนวน path ที่ผ่านเส้นเชื่อมใด ๆ มีค่าน้อยที่สุด (เราจะเรียกจำนวนผ่านที่ผ่านเส้นเชื่อมใด ๆ ว่าเป็น congestion ของเส้นเชื่อมนั้น)
คำตอบใด ๆ ของปัญหานี้ คือเซตของ path จำนวน เส้น แต่เราต้องการให้ path เหล่านี้ กระจายกันไป path เหล่านี้ทำให้เกิด congestion บนเส้นเชื่อม เป้าหมายที่เราต้องการจะทำให้มีค่าต่ำสุดของปัญหานี้คือ congestion ที่มากที่สุดบนเส้นเชื่อมใด ๆ
ถ้าเขียนให้ชัดเจนก็คือ เราต้องการจะ:
หา path:
ที่ เชื่อมระหว่าง กับ สำหรับ
เพื่อจะ minimize
เมื่อ คือจำนวน path ที่ผ่านเส้นเชื่อม
ปัญหานี้อาจจะยากสักหน่อย เราจะพิจารณาปัญหาที่ง่ายลง แทนที่เราจะ minimize ค่า congestion ที่สูงที่สุด เราจะ minimize ค่าเฉลี่ยของ congestion กล่าวคือ เราจะ:
minimize , เมื่อ แทนจำนวนเส้นเชื่อม
สังเกตว่าผลรวมของ congestion บนทุก ๆ เส้นเชื่อมนั้น เท่ากับผลรวมของความยาวของทุก ๆ path ดังนั้นเป้าหมายที่เราต้องการจะ minimize คือ
ซึ่งปัญหานี้ เราสามารถแก้ได้โดยง่าย โดยใช้อัลกอริทึมสำหรับ shortest path
สังเกตเพิ่มเติมว่า ค่าคำตอบของปัญหา average congestion minimization นี้ เป็น lower bound ของค่าของคำตอบของปัญหา congestion minimization (เพราะอะไร?) ดังนั้น ถ้าเราจะแก้ปัญหา congestion minimization โดยการใช้วิธีของปัญหาแรกเลยจะได้หรือไม่?
ถ้าเราพิจารณาให้ดี เราจะพบว่า มีตัวอย่างง่าย ๆ ที่ผลลัพธ์ที่ได้ มี congestion เท่ากับ ในขณะที่คำตอบที่ดีที่สุดให้ congestion แค่ 1 เท่านั้น
สังเกตว่าทุก ๆ path จะพยายามไปใช้เส้นทางที่สั้นที่สุดพร้อม ๆ กันหมด เราจะพยายามแก้ปัญหานี้โดยการทำให้เส้นทางที่สั้นที่สุดมีความ "น่าใช้" ลดลงเรื่อย ๆ เราจะทดลองหลาย ๆ แบบ
การปรับระยะทางแบบเชิงเส้น
เราจะปรับความยาวของ edge ตาม congestion ของ edge นั้น กล่าวคือ ในแต่ละรอบที่เราหาเส้นทางที่สั้นที่สุดเราจะให้ สำหรับทุก ๆ เส้นเชื่อม เราจะทยอยเพิ่ม path เข้าไปในระบบจนกว่าระบบจะ "นิ่ง"
เมื่อใดที่เราจะเรียกว่าระบบ "นิ่ง"? ถ้าเราเลือกเส้นทางใด เราจะเพิ่มค่า congestion ให้กับ edge บน เส้นทางนั้น ทำให้ในรอบต่อไปเวลาเราจะเลือกเส้นทางที่สั้นที่สุด เราจะเลือกได้เส้นทางอื่น ในที่นี้เราจะพิจารณาแบบง่ายไปก่อนว่า เราจะเรียกว่าระบบนิ่ง เมื่อความยาวของ path ใด ๆ เท่ากัน
สังเกตว่าในกรณีนี้ ความยาวของ edge ใน path ที่มี edge เดียว (เส้นล่างสุด) จะต้องยาวเท่ากับเส้นอื่น ๆ ทั้ง เส้น นั่นคือเราจะได้ว่า
เมื่อ คือ edge แรกใน path ที่มีจำนวน edge เท่ากับ edges (สังเกตว่าทุก ๆ edge ใน path เดี่ยวกัน จะต้องมี congestion เท่ากัน)
สังเกตว่า ผลลัพธ์ที่เราได้ จะต้องเป็น flow ที่มีขนาด k หน่วย จากจุดสมดุลย์ข้างต้น เราส่ง flow ไปแล้วทั้งสิ้นเท่ากับ
หน่วย ดังนั้นเราจะ scale flow ดังกล่าวลง เพื่อให้ได้ผลรวมเท่ากับ เราจะต้องหาตัวคูณ ที่สอดคล้องกับ
นั่นคือ
จัดนิพจน์ใหม่ ตามสมการด้านบน โดยแทนค่า เราจะได้ว่า
สังเกตว่าจำนวน flow ทั้งหมดที่ผ่านเส้นเชื่อม หลังจากการ scale ด้วย แล้ว จะมีค่าเท่ากับ
ซึ่งดีกว่าค่า congestion ในตอนแรก
การปรับระยะทางเป็นกำลังสอง
แทนที่เราจะปรับแบบเชิงเส้น เราจะปรับความยาวให้มากขึ้น โดยเราจะให้ สำหรับทุก ๆ เส้นเชื่อม
ในกรณีนี้ เราจะได้ว่า เส้นทางทุกเส้นจะมีความยาวเท่ากันก็ต่อเมื่อ
หรือ
เราแทนค่านี้ลงไปใหม่ ในการวิเคราะห์เดิมในกรณีที่ปรับค่าความยาวเป็นเชิงเสิ้น เราจะได้ว่า
ดังนั้นจำนวน flow ทั้งหมดผ่านเส้นเชื่อม หลังจากการ scale ด้วย แล้ว จะมีค่าเท่ากับ
สังเกตว่า เมื่อ ดังนั้น
ดังนั้น ค่า congestion บน หลักการ scale จะมีค่าไม่เกิน
การปรับระยะทางแบบยกกำลัง
ถ้าเราจะปรับความยาวให้มากขึ้น โดยให้ สำหรับทุก ๆ เส้นเชื่อม
ในกรณีนี้ เราจะได้ว่า เส้นทางทุกเส้นจะมีความยาวเท่ากันก็ต่อเมื่อ
หรือ เมื่อนำสมการนี้เข้าไปแทนในการวิเคราะห์เราสามารถแสดงได้ไม่ยากว่า congestion ที่มากที่สุด จะมีค่าไม่เกิน