ผลต่างระหว่างรุ่นของ "01204472/การทดลองเกี่ยวกับเวกเตอร์"

รุ่นแก้ไขปัจจุบันเมื่อ 06:03, 5 สิงหาคม 2555

การทดลองนี้เป็นส่วนหนึ่งของวิชา 01204472

เนื้อหา

1 เวกเตอร์และมุม
2 Perceptron
- 2.1 ทดลองอัลกอริทึม perceptron
- 2.2 Affine function

เวกเตอร์และมุม

เรามีข้อมูลสำหรับทดลอง 2 ชุด ดังนี้

ชุดที่ 1 มีบทความ 2 กลุ่มคือ กลุ่มของบทความในหมวด Association Football 1236 บทความ และบทความในหมวด Diets อีก 307 บทความ ดาวน์โหลด

ชุดที่ 2 มีบทความ 2 กลุ่มคือ กลุ่มของบทความในหมวด Association Football และบทความในหมวด American Football จำนวน 669 บทความ ดาวน์โหลด ดาวน์โหลดข้อมูลที่เก็บแบบ sparse

เมื่อกระจายแฟ้มข้อมูลออกมา ในนั้นจะมีแฟ้มข้อมูล นามสกุล dat อยู่ โดยแฟ้มมีหมายเลข 1xxxx.dat จะเป็นของกลุ่มแรก และ 2xxxx.dat จะเป็นของกลุ่มที่สอง แต่ละแฟ้มจะเก็บข้อมูลของ 1 เวกเตอร์ ในรูปแบบต่อไปนี้

บรรทัดแรกเก็บขนาดของเวกเตอร์
บรรทัดที่สองจะเป็นสมาชิกในเวกเตอร์ ไล่ไปทีละตัว สำหรับข้อมูลชุดนี้จะมีแค่ 0 กับ 1 เท่านั้น

ในการจัดการกับเวกเตอร์นั้น numpy มีโครงสร้างข้อมูลแบบ array ที่ทำให้เราสามารถประมวลผลได้ง่าย เราสามารถสร้างอาร์เรย์จากลิสต์ โดยสั่ง

u = array([1,2,3,4])

เราสามารถหา inner product ได้ง่าย และสามารถเรียกฟังก์ชัน norm เพื่อหา Euclidean norm ได้

หมายเหตุ เพื่อความสะดวกอย่าลืม import pylab ก่อน โดยสั่ง from pylab import *

ตัวอย่างโค้ดอ่านข้อมูลจากไฟล์มาใส่ array

def read_vector(filename):
    lines = open(filename).readlines()
    return array([float(s) for s in lines[1].strip().split()])

ส่วนที่วนลูปอ่าน vector 300 เวกเตอร์แรกของแต่ละกลุ่ม

fnums = range(10001,10301) + range(20001,20301)

vectors = {}
for f in fnums:
    vectors[f] = read_vector("%d.dat" % f)

การกระจายของมุม

ในส่วนแรกสำหรับข้อมูลแต่ละชุดเราจะวาดกราฟแสดงการกระจายของมุมที่เวกเตอร์แต่ละเวกเตอร์กระทำกับเวกเตอร์อันใดอันหนึ่ง เพื่อความรวดเร็วอาจจะใช้เวกเตอร์แค่ 300 เวกเตอร์แรกของแต่ละกลุ่มก็ได้

เราจะเลือกเวกเตอร์ในแฟ้ม 10001.dat มาเพื่อเป็นเวกเตอร์หลัก $x$ จากนั้นเราจะคำนวณมุมของ $x$ กับเวกเตอร์อื่น ๆ โดยให้วาดกราฟแสดงการกระจายของมุมระหว่างเวกเตอร์จากเอกสารในกลุ่มเดียวกัน (ในแฟ้ม 10002.dat - 10301.dat) เพื่อเปรียบเทียบกับเวกเตอร์ที่ได้จากเอกสารอีกกลุ่ม (ในแฟ้ม 20001.dat - 20301.dat)

หมายเหตุ การวาดกราฟแสดงการกระจายสามารถทำได้หลายแบบ โดยอาจจะเขียนเป็น histogram หรือนำข้อมูลมา sort แล้ว plot ตามปกติก็ได้

ให้ลองเปรียบเทียบความแตกต่างที่พบระหว่างเวกเตอร์กลุ่มที่ 1 และ 2 ในข้อมูลทั้งสองชุด

มุมเฉลี่ย

สำหรับข้อมูลแต่ละชุด เราจะคำนวณมุมเฉลี่ยระหว่าง

เวกเตอร์ในกลุ่ม 1 กับเวกเตอร์ในกลุ่ม 1 เอง
เวกเตอร์ในกลุ่ม 2 กับเวกเตอร์ในกลุ่ม 2 เอง
เวกเตอร์ในกลุ่ม 1 กับเวกเตอร์ในกลุ่ม 2

ให้ใช้วิธีการคำนวณมุมโดยคำนวณโดยตรง จากนั้นเปรียบเทียบ "ความแตกต่าง" ของมุมเฉลี่ยทั้ง 3 แบบ ที่ได้จากข้อมูลชุด 1 กับชุดที่ 2

มุมเฉลี่ย: sparse vector

เวกเตอร์ที่เราสนใจมีลักษณะพิเศษ กล่าวคือ ถืงแม้เวกเตอร์จะมีขนาดใหญ่ แต่สมาชิกในเวกเตอร์แทบทั้งหมดคือ 0 ดังนั้น การคำนวณโดยตรงกับเวกเตอร์ประเภทนี้โดยมากจึงกลายเป็นงานสูญเปล่า

ให้เปลี่ยนวิธีการเก็บเวกเตอร์สำหรับการหา inner product โดยแทนที่จะเก็บเป็น array อาจเปลี่ยนเป็นโครงสร้างข้อมูลอื่น (hint: dict หรืออาจจะใช้วิธีอื่น ๆ ก็ได้)

เมื่อเราเปลี่ยนวิธีการเก็บเวกเตอร์ใหม่แล้ว การคำนวณ inner product เพื่อหามุมอาจจะต้องเปลี่ยนไปด้วย ให้แก้โปรแกรม จากนั้นให้คำนวณมุมเฉลี่ยใหม่อีกครั้งและเปรียบเทียบเวลาที่ใช้กับเวลาที่ใช้เมื่อเราคำนวณโดยตรง

หมายเหตุ ในข้อนี้ถ้าใครอยากนึกสนุก สามารถลองเขียนเทียบเวลาการคำนวณเมื่อใช้ภาษาอื่น ๆ ที่เร็วกว่าได้ เช่น C++, Java, หรือ C#

Perceptron

ในข้อนี้เราจะต้องพล็อตกราฟแบบจุด ดูตัวอย่างการใช้งานและโปรแกรมสำหรับพล็อตอย่างง่าย ได้จากตอนท้ายของหน้า 01204472/ตัวอย่าง_matplotlib

เรามีข้อมูลสำหรับทดลอง 4 ชุด ในแฟ้ม p1.txt, p2.txt, p3.txt, และ p4.txt เข้าไปดาวน์โหลดที่นี่ นิสิตสามารถโหลดมาแล้วพล็อตดูข้อมูลก่อนโดยใช้ตัวอย่างโปรแกรมจากหน้า 01204472/ตัวอย่าง_matplotlib ได้

เมื่อลองพล็อตดูแล้ว ให้นิสิตลองพิจารณาว่า function ที่จะแบ่งข้อมูลทั้งสองกลุ่มออกจากการควรจะมีลักษณะอย่างใด

ทดลองอัลกอริทึม perceptron

ในส่วนนี้เราจะทดลอง implement อัลกอริทึม Perceptron

แม้ว่าอัลกอริทึมดังกล่าวจะเป็นอัลกอริทึมแบบออนไลน์ แต่เราจะทดลองกับข้อมูลทั้ง 4 ชุดแบบ batch กล่าวคือ

เราจะใช้อัลกอริทึมดังกล่าวในการหาเวกเตอร์ $w$ ที่ inner product ของ $w$ กับเวกเตอร์ในกลุ่ม 1 มีค่าไม่เป็นลบ แต่ inner product ของ $w$ กับเวกเตอร์ในกลุ่ม 2 มีค่าเป็นลบ
ในการหาเวกเตอร์ $w$ เราจะใส่ข้อมูลทุกตัวในแฟ้มข้อมูลให้กับ Perceptron algorithm เป็นรอบ ๆ จนครบ
ในแต่ละรอบ ให้นับจำนวนครั้งที่อัลกอริทึมทำนายพลาด เพื่อดูประสิทธิภาพของเวกเตอร์ $w$ กับข้อมูลตัวอย่าง
ทดลอง 10 รอบ หรือจนกว่าจะตอบได้ถูกหมด (ซึ่งหลังจากนั้นจะไม่มีการปรับค่า)

ในการ implement นั้น ให้เขียนโปรแกรมที่ทำงานกับเวกเตอร์ทั่วไปได้ (แม้ว่าตัวอย่างจะเป็นเวกเตอร์ที่มีขนาด 2 ก็ตาม เพราะว่าในข้อถัดไปเราจะปรับแต่งเวกเตอร์เล็กน้อย)

สำหรับข้อมูลแต่ละชุด พล็อตข้อมูล พร้อมทั้งวาดเวกเตอร์ $w$ และเวกเตอร์ที่ตั้งฉากกับ $w$ ดังตัวอย่างด้านล่าง

หมายเหตุในการเขียน:

ถ้าต้องการใช้ array เพื่อจัดเก็บเวกเตอร์ สามารถสั่ง from numpy import *
เวกเตอร์ในรูปแสดงโดยใช้ฟังก์ชัน plot อย่างไรก็ตามในหลายข้อ เวกเตอร์ที่ได้มีขนาดใหญ่มาก อาจจำเป็นต้อง scale เวกเตอร์ก่อน
ถ้าต้องการใช้ฟังก์ชัน norm เพื่อหา Euclidean norm ของเวกเตอร์ สามารถสั่ง from numpy.linalg import *
ถ้าต้องการลากเส้นแกน ลองสั่งคำสั่ง plt.axhline() และ plt.axvline() ได้ คำสั่งทั้งสองปรับสีได้ด้วยถ้าเพิ่มพารามิเตอร์เช่น c='gray' เข้าไป

Affine function

ถ้าเราพิจารณาข้อมูลชุดที่ 3 และ 4 เราจะพบว่า เราสามารถขีดเส้นตรงแบ่งข้อมูลเป็นสองกลุ่มได้ แต่ฟังก์ชันของเส้นทั้งสองนั้นไม่ใช่ฟังก์ชันเชิงเส้น แต่เป็น affine function

เรายังสามารถปรับให้อัลกอริทึม Perceptron ทำงานในกรณีดังกล่าวได้ โดยเพิ่มขนาดให้กับเวกเตอร์ที่เราสนใจทั้งหมด จาก 2 เป็น 3 โดยสำหรับเวกเตอร์ข้อมูลตัวอย่าง เราจะเพิ่ม 1 เป็นสมาชิกตัวที่ 3 เช่น จากจุด (10,2) เราจะใช้เป็นจุด (1,2,1) และเวกเตอร์ $w$ เราก็จะให้มีขนาดเป็น 3 ด้วยเช่นกัน

ปรับโปรแกรมตามที่ระบุข้างต้นและทดลอง โดยในตัวอย่างที่ 3 และ 4 อาจจะต้องทดลองโดยเพิ่มจำนวนรอบที่มากหน่อย (ไม่เกิน 100 รอบ) ก็จะสามารถหาเวกเตอร์ $w$ ได้

ให้พยายามอธิบายว่าทำไมการแก้ไขดังกล่าวจึงทำให้ Perceptron ทำงานได้ในกรณีที่เส้นแบ่งเป็น affine function

หมายเหตุ อาจจะทดลองพล็อตแบบสามมิติเพื่อดูตำแหน่งของจุดและทิศทางของเวกเตอร์ $w$ ก็ได้

@@ แถว 2: / แถว 2: @@
 == เวกเตอร์และมุม ==
-=== มุมเฉลี่ย ===
 เรามีข้อมูลสำหรับทดลอง 2 ชุด ดังนี้
@@ แถว 10: / แถว 8: @@
 * ชุดที่ 2 มีบทความ 2 กลุ่มคือ กลุ่มของบทความในหมวด [http://en.wikipedia.org/wiki/Category:Association_football Association Football] และบทความในหมวด [http://en.wikipedia.org/wiki/Category:American_football American Football] จำนวน 669 บทความ [http://theory.cpe.ku.ac.th/~jittat/01204472-55/vectors/football-full.tgz ดาวน์โหลด] [http://theory.cpe.ku.ac.th/~jittat/01204472-55/vectors/football-sparse.tgz ดาวน์โหลดข้อมูลที่เก็บแบบ sparse]
+เมื่อกระจายแฟ้มข้อมูลออกมา ในนั้นจะมีแฟ้มข้อมูล นามสกุล dat อยู่ โดยแฟ้มมีหมายเลข 1xxxx.dat จะเป็นของกลุ่มแรก และ 2xxxx.dat จะเป็นของกลุ่มที่สอง  แต่ละแฟ้มจะเก็บข้อมูลของ 1 เวกเตอร์ ในรูปแบบต่อไปนี้
+* บรรทัดแรกเก็บขนาดของเวกเตอร์
+* บรรทัดที่สองจะเป็นสมาชิกในเวกเตอร์ ไล่ไปทีละตัว  สำหรับข้อมูลชุดนี้จะมีแค่ 0 กับ 1 เท่านั้น
+ในการจัดการกับเวกเตอร์นั้น numpy มีโครงสร้างข้อมูลแบบ array ที่ทำให้เราสามารถประมวลผลได้ง่าย เราสามารถสร้างอาร์เรย์จากลิสต์ โดยสั่ง
+ u = array([1,2,3,4])
+เราสามารถหา inner product ได้ง่าย และสามารถเรียกฟังก์ชัน <tt>norm</tt> เพื่อหา Euclidean norm ได้
+'''หมายเหตุ''' เพื่อความสะดวกอย่าลืม import pylab ก่อน โดยสั่ง <tt>from pylab import *</tt>
+ตัวอย่างโค้ดอ่านข้อมูลจากไฟล์มาใส่ array
+<pre>
+def read_vector(filename):
+    lines = open(filename).readlines()
+    return array([float(s) for s in lines[1].strip().split()])
+</pre>
+ส่วนที่วนลูปอ่าน vector 300 เวกเตอร์แรกของแต่ละกลุ่ม
+<pre>
+fnums = range(10001,10301) + range(20001,20301)
+vectors = {}
+for f in fnums:
+    vectors[f] = read_vector("%d.dat" % f)
+</pre>
 === การกระจายของมุม ===
+ในส่วนแรกสำหรับข้อมูลแต่ละชุดเราจะวาดกราฟแสดงการกระจายของมุมที่เวกเตอร์แต่ละเวกเตอร์กระทำกับเวกเตอร์อันใดอันหนึ่ง  เพื่อความรวดเร็วอาจจะใช้เวกเตอร์แค่ 300 เวกเตอร์แรกของแต่ละกลุ่มก็ได้
+เราจะเลือกเวกเตอร์ในแฟ้ม 10001.dat มาเพื่อเป็นเวกเตอร์หลัก <math>x</math> จากนั้นเราจะคำนวณมุมของ <math>x</math> กับเวกเตอร์อื่น ๆ โดยให้วาดกราฟแสดงการกระจายของมุมระหว่างเวกเตอร์จากเอกสารในกลุ่มเดียวกัน (ในแฟ้ม 10002.dat - 10301.dat) เพื่อเปรียบเทียบกับเวกเตอร์ที่ได้จากเอกสารอีกกลุ่ม (ในแฟ้ม 20001.dat - 20301.dat)
+'''หมายเหตุ''' การวาดกราฟแสดงการกระจายสามารถทำได้หลายแบบ โดยอาจจะเขียนเป็น histogram หรือนำข้อมูลมา sort แล้ว plot ตามปกติก็ได้
+ให้ลองเปรียบเทียบความแตกต่างที่พบระหว่างเวกเตอร์กลุ่มที่ 1 และ 2 ในข้อมูลทั้งสองชุด
+=== มุมเฉลี่ย ===
+สำหรับข้อมูลแต่ละชุด เราจะคำนวณมุมเฉลี่ยระหว่าง
+* เวกเตอร์ในกลุ่ม 1 กับเวกเตอร์ในกลุ่ม 1 เอง
+* เวกเตอร์ในกลุ่ม 2 กับเวกเตอร์ในกลุ่ม 2 เอง
+* เวกเตอร์ในกลุ่ม 1 กับเวกเตอร์ในกลุ่ม 2
+ให้ใช้วิธีการคำนวณมุมโดยคำนวณโดยตรง  จากนั้นเปรียบเทียบ "ความแตกต่าง" ของมุมเฉลี่ยทั้ง 3 แบบ ที่ได้จากข้อมูลชุด 1 กับชุดที่ 2
+=== มุมเฉลี่ย: sparse vector ===
+เวกเตอร์ที่เราสนใจมีลักษณะพิเศษ กล่าวคือ ถืงแม้เวกเตอร์จะมีขนาดใหญ่ แต่สมาชิกในเวกเตอร์แทบทั้งหมดคือ 0   ดังนั้น การคำนวณโดยตรงกับเวกเตอร์ประเภทนี้โดยมากจึงกลายเป็นงานสูญเปล่า
+ให้เปลี่ยนวิธีการเก็บเวกเตอร์สำหรับการหา inner product โดยแทนที่จะเก็บเป็น <tt>array</tt> อาจเปลี่ยนเป็นโครงสร้างข้อมูลอื่น (hint: [http://docs.python.org/tutorial/datastructures.html#dictionaries dict] หรืออาจจะใช้วิธีอื่น ๆ ก็ได้)
+เมื่อเราเปลี่ยนวิธีการเก็บเวกเตอร์ใหม่แล้ว การคำนวณ inner product เพื่อหามุมอาจจะต้องเปลี่ยนไปด้วย  ให้แก้โปรแกรม จากนั้นให้คำนวณมุมเฉลี่ยใหม่อีกครั้งและเปรียบเทียบเวลาที่ใช้กับเวลาที่ใช้เมื่อเราคำนวณโดยตรง
+'''หมายเหตุ''' ในข้อนี้ถ้าใครอยากนึกสนุก สามารถลองเขียนเทียบเวลาการคำนวณเมื่อใช้ภาษาอื่น ๆ ที่เร็วกว่าได้ เช่น C++, Java, หรือ C#
+== Perceptron ==
+: ''ในข้อนี้เราจะต้องพล็อตกราฟแบบจุด ดูตัวอย่างการใช้งานและโปรแกรมสำหรับพล็อตอย่างง่าย ได้จากตอนท้ายของหน้า [[01204472/ตัวอย่าง_matplotlib]]''
+เรามีข้อมูลสำหรับทดลอง 4 ชุด ในแฟ้ม p1.txt, p2.txt, p3.txt, และ p4.txt [http://theory.cpe.ku.ac.th/~jittat/01204472-55/vectors/ เข้าไปดาวน์โหลดที่นี่]  นิสิตสามารถโหลดมาแล้วพล็อตดูข้อมูลก่อนโดยใช้ตัวอย่างโปรแกรมจากหน้า [[01204472/ตัวอย่าง_matplotlib]] ได้
+เมื่อลองพล็อตดูแล้ว ให้นิสิตลองพิจารณาว่า function ที่จะแบ่งข้อมูลทั้งสองกลุ่มออกจากการควรจะมีลักษณะอย่างใด
+=== ทดลองอัลกอริทึม perceptron ===
+ในส่วนนี้เราจะทดลอง implement [[01204472/perceptron_algorithm|อัลกอริทึม Perceptron]]
+แม้ว่าอัลกอริทึมดังกล่าวจะเป็นอัลกอริทึมแบบออนไลน์ แต่เราจะทดลองกับข้อมูลทั้ง 4 ชุดแบบ batch กล่าวคือ
+*เราจะใช้อัลกอริทึมดังกล่าวในการหาเวกเตอร์ <math>w</math> ที่ inner product ของ <math>w</math> กับเวกเตอร์ในกลุ่ม 1 มีค่าไม่เป็นลบ แต่ inner product ของ <math>w</math> กับเวกเตอร์ในกลุ่ม 2 มีค่าเป็นลบ
+* ในการหาเวกเตอร์ <math>w</math> เราจะใส่ข้อมูลทุกตัวในแฟ้มข้อมูลให้กับ Perceptron algorithm เป็นรอบ ๆ จนครบ
+* ในแต่ละรอบ ให้นับจำนวนครั้งที่อัลกอริทึมทำนายพลาด เพื่อดูประสิทธิภาพของเวกเตอร์ <math>w</math> กับข้อมูลตัวอย่าง
+* ทดลอง 10 รอบ หรือจนกว่าจะตอบได้ถูกหมด (ซึ่งหลังจากนั้นจะไม่มีการปรับค่า)
+ในการ implement นั้น ให้เขียนโปรแกรมที่ทำงานกับเวกเตอร์ทั่วไปได้ (แม้ว่าตัวอย่างจะเป็นเวกเตอร์ที่มีขนาด 2 ก็ตาม เพราะว่าในข้อถัดไปเราจะปรับแต่งเวกเตอร์เล็กน้อย)
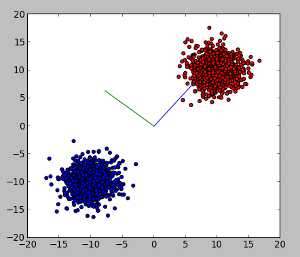
+สำหรับข้อมูลแต่ละชุด พล็อตข้อมูล พร้อมทั้งวาดเวกเตอร์ <math>w</math> และเวกเตอร์ที่ตั้งฉากกับ <math>w</math> ดังตัวอย่างด้านล่าง
+[[Image:Perceptron-w-vectors.png]]
+'''หมายเหตุในการเขียน''':
+* ถ้าต้องการใช้ <tt>array</tt> เพื่อจัดเก็บเวกเตอร์ สามารถสั่ง <tt>from numpy import *</tt>
+* เวกเตอร์ในรูปแสดงโดยใช้ฟังก์ชัน <tt>plot</tt>  อย่างไรก็ตามในหลายข้อ เวกเตอร์ที่ได้มีขนาดใหญ่มาก อาจจำเป็นต้อง scale เวกเตอร์ก่อน
+* ถ้าต้องการใช้ฟังก์ชัน <tt>norm</tt> เพื่อหา Euclidean norm ของเวกเตอร์ สามารถสั่ง <tt>from numpy.linalg import *</tt>
+* ถ้าต้องการลากเส้นแกน ลองสั่งคำสั่ง <tt>plt.axhline()</tt> และ <tt>plt.axvline()</tt> ได้ คำสั่งทั้งสองปรับสีได้ด้วยถ้าเพิ่มพารามิเตอร์เช่น <tt>c='gray'</tt> เข้าไป
+=== Affine function ===
+ถ้าเราพิจารณาข้อมูลชุดที่ 3 และ 4 เราจะพบว่า เราสามารถขีดเส้นตรงแบ่งข้อมูลเป็นสองกลุ่มได้ แต่ฟังก์ชันของเส้นทั้งสองนั้นไม่ใช่ฟังก์ชันเชิงเส้น แต่เป็น affine function
+เรายังสามารถปรับให้อัลกอริทึม Perceptron ทำงานในกรณีดังกล่าวได้ โดยเพิ่มขนาดให้กับเวกเตอร์ที่เราสนใจทั้งหมด จาก 2 เป็น 3 โดยสำหรับเวกเตอร์ข้อมูลตัวอย่าง เราจะเพิ่ม 1 เป็นสมาชิกตัวที่ 3 เช่น จากจุด (10,2) เราจะใช้เป็นจุด (1,2,1) และเวกเตอร์ <math>w</math> เราก็จะให้มีขนาดเป็น 3 ด้วยเช่นกัน
+ปรับโปรแกรมตามที่ระบุข้างต้นและทดลอง โดยในตัวอย่างที่ 3 และ 4 อาจจะต้องทดลองโดยเพิ่มจำนวนรอบที่มากหน่อย (ไม่เกิน 100 รอบ) ก็จะสามารถหาเวกเตอร์ <math>w</math> ได้
+ให้พยายามอธิบายว่าทำไมการแก้ไขดังกล่าวจึงทำให้ Perceptron ทำงานได้ในกรณีที่เส้นแบ่งเป็น affine function
+'''หมายเหตุ''' อาจจะทดลองพล็อตแบบสามมิติเพื่อดูตำแหน่งของจุดและทิศทางของเวกเตอร์ <math>w</math> ก็ได้

ผลต่างระหว่างรุ่นของ "01204472/การทดลองเกี่ยวกับเวกเตอร์"

รุ่นแก้ไขปัจจุบันเมื่อ 06:03, 5 สิงหาคม 2555

เนื้อหา

เวกเตอร์และมุม

การกระจายของมุม

มุมเฉลี่ย

มุมเฉลี่ย: sparse vector

Perceptron

ทดลองอัลกอริทึม perceptron

Affine function

รายการเลือกการนำทาง

เครื่องมือส่วนตัว

เนมสเปซ

สิ่งที่แตกต่าง

ดู

เพิ่มเติม

ค้นหา

การนำทาง

เครื่องมือ