ผลต่างระหว่างรุ่นของ "01204472/การทดลองเกี่ยวกับ SVD"
ไปยังการนำทาง
ไปยังการค้นหา
Jittat (คุย | มีส่วนร่วม) |
Jittat (คุย | มีส่วนร่วม) |
||
| แถว 18: | แถว 18: | ||
[[image:Cir-eig.png]] | [[image:Cir-eig.png]] | ||
| + | |||
| + | ให้หา eigenvector ของ M ด้วยฟังก์ชัน [http://docs.scipy.org/doc/numpy/reference/generated/numpy.linalg.eig.html eig] เวกเตอร์ดังกล่าวอธิบายอะไรเกี่ยวกับรูปด้านบน | ||
| + | |||
| + | ให้ลองคูณ M เข้ากับ eigen vector ที่ได้ทั้งสอง | ||
| + | |||
| + | ให้ plot eigen vector ทั้งสองลงบนกราฟ (สังเกตว่าเวกเตอร์ไม่จำเป็นต้องตั้งฉากกัน) | ||
| + | |||
| + | === SVD ของ M === | ||
== เมตริกซ์ที่มี Low rank == | == เมตริกซ์ที่มี Low rank == | ||
รุ่นแก้ไขเมื่อ 02:33, 6 กันยายน 2555
เนื้อหา
ทดลองเกี่ยวกับ eigenvectors
ก่อนอื่นเราจะสร้างรายการของจุดบนวงกลมรัศมี 1 หน่วย
ang = arange(0,2.*pi,pi/10.) x = [cos(a) for a in ang] y = [sin(a) for a in ang]
plot(x,y,'o')
สร้างรายการของเวกเตอร์จากลิสต์ x และ y
vs = [matrix([[xx],[yy]]) for xx,yy in zip(x,y)]
จากนั้นให้สร้างเมตริกซ์ M ขนาด 2x2 ขึ้นมา สำหรับเวกเตอร์ v แต่ละเวกเตอร์ใน vs ให้หา Mv และรวมเป็นรายการ mvs
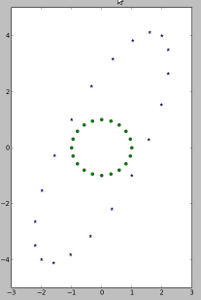
ให้นำจุดเหล่านั้นในลิสต์ mvs มา plot ที่เดียวกับจุดจากรายการ vs ที่เรา plot ตอนแรก ดังตัวอย่างด้านล่าง (รูปอาจจะไม่เหมือน ขึ้นกับเมตริกซ์ M)
ให้หา eigenvector ของ M ด้วยฟังก์ชัน eig เวกเตอร์ดังกล่าวอธิบายอะไรเกี่ยวกับรูปด้านบน
ให้ลองคูณ M เข้ากับ eigen vector ที่ได้ทั้งสอง
ให้ plot eigen vector ทั้งสองลงบนกราฟ (สังเกตว่าเวกเตอร์ไม่จำเป็นต้องตั้งฉากกัน)
SVD ของ M
เมตริกซ์ที่มี Low rank
การประมาณเมตริกซ์ ด้วย Low rank เมตริกซ์
Collaborative filtering
อ่านเพิ่มเติม: http://www.netflixprize.com/community/viewtopic.php?id=1043