ผลต่างระหว่างรุ่นของ "01204472/การทดลองเกี่ยวกับ SVD"

จาก Theory Wiki
ไปยังการนำทาง ไปยังการค้นหา
 
(ไม่แสดง 17 รุ่นระหว่างกลางโดยผู้ใช้คนเดียวกัน)
แถว 1: แถว 1:
 +
ในการทดลองวันนี้เราจะ plot กราฟเป็นจำนวนมาก โดยปกติเมื่อเราสั่ง plot กราฟที่ได้จะทับกับรูปเดิม ถ้าเราต้องการสร้าง figure ใหม่ (เพื่อเก็บรูปเดิมไว้) ให้สั่ง
 +
 +
figure()
 +
 
== ทดลองเกี่ยวกับ eigenvectors ==
 
== ทดลองเกี่ยวกับ eigenvectors ==
  
แถว 18: แถว 22:
  
 
[[image:Cir-eig.png]]
 
[[image:Cir-eig.png]]
 +
 +
ให้หา eigenvector ของ M ด้วยฟังก์ชัน [http://docs.scipy.org/doc/numpy/reference/generated/numpy.linalg.eig.html eig] เวกเตอร์ดังกล่าวอธิบายอะไรเกี่ยวกับรูปด้านบน
 +
 +
ให้ลองคูณ M เข้ากับ eigenvector ที่ได้ทั้งสอง
 +
 +
ให้ plot eigenvector ทั้งสองลงบนกราฟ (สังเกตว่าเวกเตอร์ไม่จำเป็นต้องตั้งฉากกัน)
  
 
== เมตริกซ์ที่มี Low rank ==
 
== เมตริกซ์ที่มี Low rank ==
  
 +
เราจะทดลองสร้างเมตริกซ์ที่มี rank ต่ำ
 +
 +
สร้างเวกเตอร์ X
 +
 +
X = matrix([ [sin(a) for a in arange(0,4*pi,pi/50)] ]).T
 +
 +
และเวกเตอร์ Y
 +
 +
Y = matrix([ [cos(a) for a in arange(0,4*pi,pi/50)] ]).T
 +
 +
สร้างเมตริกซ์ M โดยให้เท่ากับ X Y<sup>T</sup>
 +
 +
M = X * Y.T
 +
 +
จากให้แสดงเมตริกซ์ดังกล่าวด้วยคำสั่ง
 +
 +
imshow(M)
 +
 +
Rank ของเมตริกซ์ M มีค่าเท่ากับเท่าใด?
 +
 +
ทดลองคำนวณ rank ของ M ด้วยคำสั่ง <tt>matrix_rank(M)</tt> (อย่าสับสนกับฟังก์ชัน rank) ทำไมผลลัพธ์ที่ได้ไม่ตรงกับที่เราคาดการณ์ไว้?
 +
 +
ให้คำนวณหา singular value decomposition ของ M โดยสั่ง
 +
 +
u,s,v = svd(M)
 +
 +
ให้พิจารณาค่าใน s  ค่าดังกล่าวเกี่ยวข้องอะไรกับ rank ของ M?
 +
 +
พิจารณาเมตริกซ์ u, ทดลองสั่ง plot คอลัมน์แรกของ u
 +
 +
plot(u[:,0])
 +
 +
พิจารณาเมตริกซ์ v, ทดลองสั่ง plot แถวแรกของ v
 +
 +
plot(v[0,:].T)
  
 
== การประมาณเมตริกซ์ ด้วย Low rank เมตริกซ์ ==
 
== การประมาณเมตริกซ์ ด้วย Low rank เมตริกซ์ ==
 +
เราจะสร้างเมตริกซ์ N ที่เป็น noise ขนาด 0.01
 +
 +
N = matrix([[uniform()/100. for i in range(200)] for j in range(200)])
 +
 +
จากเมตริกซ์ M ในตัวอย่างที่แล้ว ให้สร้าง
 +
 +
MM = M + N
 +
 +
ทดลอง plot
 +
 +
imshow(MM)
 +
 +
สังเกตว่า MM มีลักษณะใกล้เคียงกับ M มาก  ทดลองหา rank โดยสั่ง
 +
 +
matrix_rank(MM)
 +
 +
ค่าดังกล่าวบอกอะไรกับเรา? เมตริกซ์ M กับ MM ต่างกันอย่างไร?
 +
 +
decompose MM ด้วย SVD
 +
 +
a,b,c = svd(MM)
 +
 +
พิจารณาเวกเตอร์ b, คอลัมน์แรกของ a, แถวแรกของ c (ทดลอง plot ค่าดู)
 +
 +
เราจะสร้างเมตริกซ์ MMM ที่ approximate MM ที่มี rank = 1 ได้อย่างไร?
 +
 +
ทดลองสร้าง MMM แล้ว plot ผลลัพธ์ด้วย imshow
 +
 +
=== ทดลองโดยการเพิ่ม noise ===
 +
 +
ทดลองซ้ำ โดยเพิ่ม noise ให้มากขึ้นเป็นระดับ 1 หน่วย โดยสั่ง
 +
 +
N = matrix([[uniform() for i in range(200)] for j in range(200)])
 +
 +
ให้
 +
 +
MM = M + N
 +
 +
จากนั้นคำนวณ
 +
 +
a,b,c = svd(MM)
 +
 +
พิจารณาค่าในเวกเตอร์ b  เวกเตอร์ b ที่ได้ ต่างจากกรณีที่หาเมื่อระดับของ noise ต่ำ ๆ อย่างไร?
 +
 +
สร้างเมตริกซ์ที่ approximate MM ที่มี rank = 1 สังเกตผลโดยสั่ง imshow
 +
 +
ผลลัพธ์ที่ได้ใกล้เคียงกับ M หรือไม่ อย่างไร?
 +
 +
สร้างเมตริกซ์ที่ approximate MM ที่มี rank = 2 สังเกตผลโดยสั่ง imshow
 +
 +
สร้างเมตริกซ์ที่ approximate MM ที่มี rank = 3 สังเกตผลโดยสั่ง imshow
  
 +
'''หมายเหตุ:''' การสร้าง matrix ที่ approximate MM ข้าง ต้นสามารถสั่งได้ด้วยคำสั่งเดียว
  
 
== Collaborative filtering ==
 
== Collaborative filtering ==
  
−
อ่านเพิ่มเติม: http://www.netflixprize.com/community/viewtopic.php?id=1043
+
* [http://ict.ewi.tudelft.nl/~jun/CollaborativeFiltering.html Collborative Filtering Resources]
 +
* [http://www.netflixprize.com/community/viewtopic.php?id=1043 A guide to SVD for collaborative filtering]

รุ่นแก้ไขปัจจุบันเมื่อ 09:16, 6 กันยายน 2555

ในการทดลองวันนี้เราจะ plot กราฟเป็นจำนวนมาก โดยปกติเมื่อเราสั่ง plot กราฟที่ได้จะทับกับรูปเดิม ถ้าเราต้องการสร้าง figure ใหม่ (เพื่อเก็บรูปเดิมไว้) ให้สั่ง 

figure()

ทดลองเกี่ยวกับ eigenvectors

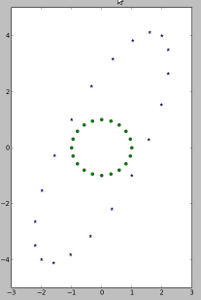
ก่อนอื่นเราจะสร้างรายการของจุดบนวงกลมรัศมี 1 หน่วย 

ang = arange(0,2.*pi,pi/10.)
x = [cos(a) for a in ang]
y = [sin(a) for a in ang]

plot(x,y,'o')

สร้างรายการของเวกเตอร์จากลิสต์ x และ y 

vs = [matrix([[xx],[yy]]) for xx,yy in zip(x,y)]

จากนั้นให้สร้างเมตริกซ์ M ขนาด 2x2 ขึ้นมา สำหรับเวกเตอร์ v แต่ละเวกเตอร์ใน vs ให้หา Mv และรวมเป็นรายการ mvs

ให้นำจุดเหล่านั้นในลิสต์ mvs มา plot ที่เดียวกับจุดจากรายการ vs ที่เรา plot ตอนแรก ดังตัวอย่างด้านล่าง (รูปอาจจะไม่เหมือน ขึ้นกับเมตริกซ์ M)

Cir-eig.png

ให้หา eigenvector ของ M ด้วยฟังก์ชัน eig เวกเตอร์ดังกล่าวอธิบายอะไรเกี่ยวกับรูปด้านบน

ให้ลองคูณ M เข้ากับ eigenvector ที่ได้ทั้งสอง

ให้ plot eigenvector ทั้งสองลงบนกราฟ (สังเกตว่าเวกเตอร์ไม่จำเป็นต้องตั้งฉากกัน)

เมตริกซ์ที่มี Low rank

เราจะทดลองสร้างเมตริกซ์ที่มี rank ต่ำ

สร้างเวกเตอร์ X 

X = matrix([ [sin(a) for a in arange(0,4*pi,pi/50)] ]).T

และเวกเตอร์ Y 

Y = matrix([ [cos(a) for a in arange(0,4*pi,pi/50)] ]).T

สร้างเมตริกซ์ M โดยให้เท่ากับ X YT 

M = X * Y.T

จากให้แสดงเมตริกซ์ดังกล่าวด้วยคำสั่ง 

imshow(M)

Rank ของเมตริกซ์ M มีค่าเท่ากับเท่าใด?

ทดลองคำนวณ rank ของ M ด้วยคำสั่ง matrix_rank(M) (อย่าสับสนกับฟังก์ชัน rank) ทำไมผลลัพธ์ที่ได้ไม่ตรงกับที่เราคาดการณ์ไว้?

ให้คำนวณหา singular value decomposition ของ M โดยสั่ง 

u,s,v = svd(M)

ให้พิจารณาค่าใน s ค่าดังกล่าวเกี่ยวข้องอะไรกับ rank ของ M?

พิจารณาเมตริกซ์ u, ทดลองสั่ง plot คอลัมน์แรกของ u 

plot(u[:,0])

พิจารณาเมตริกซ์ v, ทดลองสั่ง plot แถวแรกของ v 

plot(v[0,:].T)

การประมาณเมตริกซ์ ด้วย Low rank เมตริกซ์

เราจะสร้างเมตริกซ์ N ที่เป็น noise ขนาด 0.01 

N = matrix([[uniform()/100. for i in range(200)] for j in range(200)])

จากเมตริกซ์ M ในตัวอย่างที่แล้ว ให้สร้าง 

MM = M + N

ทดลอง plot 

imshow(MM)

สังเกตว่า MM มีลักษณะใกล้เคียงกับ M มาก ทดลองหา rank โดยสั่ง 

matrix_rank(MM)

ค่าดังกล่าวบอกอะไรกับเรา? เมตริกซ์ M กับ MM ต่างกันอย่างไร?

decompose MM ด้วย SVD 

a,b,c = svd(MM)

พิจารณาเวกเตอร์ b, คอลัมน์แรกของ a, แถวแรกของ c (ทดลอง plot ค่าดู)

เราจะสร้างเมตริกซ์ MMM ที่ approximate MM ที่มี rank = 1 ได้อย่างไร?

ทดลองสร้าง MMM แล้ว plot ผลลัพธ์ด้วย imshow

ทดลองโดยการเพิ่ม noise

ทดลองซ้ำ โดยเพิ่ม noise ให้มากขึ้นเป็นระดับ 1 หน่วย โดยสั่ง 

N = matrix([[uniform() for i in range(200)] for j in range(200)])

ให้ 

MM = M + N

จากนั้นคำนวณ 

a,b,c = svd(MM)

พิจารณาค่าในเวกเตอร์ b เวกเตอร์ b ที่ได้ ต่างจากกรณีที่หาเมื่อระดับของ noise ต่ำ ๆ อย่างไร?

สร้างเมตริกซ์ที่ approximate MM ที่มี rank = 1 สังเกตผลโดยสั่ง imshow

ผลลัพธ์ที่ได้ใกล้เคียงกับ M หรือไม่ อย่างไร?

สร้างเมตริกซ์ที่ approximate MM ที่มี rank = 2 สังเกตผลโดยสั่ง imshow

สร้างเมตริกซ์ที่ approximate MM ที่มี rank = 3 สังเกตผลโดยสั่ง imshow

หมายเหตุ: การสร้าง matrix ที่ approximate MM ข้าง ต้นสามารถสั่งได้ด้วยคำสั่งเดียว

Collaborative filtering

ดึงข้อมูลจาก "http://158.108.32.49/wiki/index.php?title=01204472/การทดลองเกี่ยวกับ_SVD&oldid=36533"