ผลต่างระหว่างรุ่นของ "Probstat/week15 practice 1"
ไปยังการนำทาง
ไปยังการค้นหา
Jittat (คุย | มีส่วนร่วม) (หน้าที่ถูกสร้างด้วย 'Generate 5 sets of samples from normal populations, each of size 10, on a spreadsheet software. Make sure that the mean and variance o...') |
Jittat (คุย | มีส่วนร่วม) (→Test) |
||
| (ไม่แสดง 8 รุ่นระหว่างกลางโดยผู้ใช้คนเดียวกัน) | |||
| แถว 1: | แถว 1: | ||
| + | : ''This is part of [[probstat]].'' | ||
| + | |||
| + | == Data generation == | ||
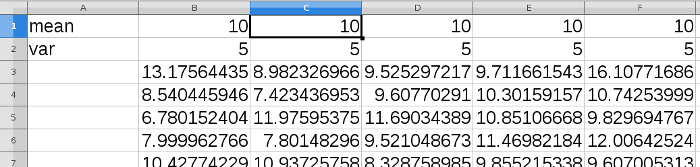
Generate 5 sets of samples from normal populations, each of size 10, on a spreadsheet software. Make sure that the mean and variance of each set can be modified easily. | Generate 5 sets of samples from normal populations, each of size 10, on a spreadsheet software. Make sure that the mean and variance of each set can be modified easily. | ||
| + | |||
| + | [[Image:Prob-anova-data.png]] | ||
| + | |||
| + | == Variance estimations == | ||
| + | '''Estimator 1.''' The first estimator for <math>\sigma^2</math> is | ||
| + | |||
| + | <center> | ||
| + | <math>\frac{1}{m}\sum_{i=1}^m \sum_{j=1}^n \frac{(X_{ij} - \bar{X}_{i\centerdot})^2}{n-1}.</math> | ||
| + | </center> | ||
| + | |||
| + | This estimator is always correct. (Even when <math>H_0</math> is not true.) | ||
| + | |||
| + | '''Estimator 2.''' The second estimator is calculated from the sample means. It will be correct only when <math>H_0</math> is true. | ||
| + | |||
| + | <center> | ||
| + | <math>n \sum_{i=1}^m \frac{(\bar{X}_{i\centerdot} - \bar{X}_{\centerdot\centerdot})^2}{m-1}</math> | ||
| + | </center> | ||
| + | |||
| + | == Hypothesis testing == | ||
| + | Then compute | ||
| + | |||
| + | <center> | ||
| + | <math>SS_w = \sum_{i=1}^m \sum_{j=1}^n (X_{ij} - \bar{X}_{i\centerdot})^2</math> | ||
| + | </center> | ||
| + | |||
| + | and | ||
| + | |||
| + | <center> | ||
| + | <math>SS_b = n \sum_{i=1}^m (\bar{X}_{i\centerdot} - \bar{X}_{\centerdot\centerdot})^2</math> | ||
| + | </center> | ||
| + | |||
| + | Recall that | ||
| + | |||
| + | <center> | ||
| + | <math>\frac{SS_w}{\sigma^2} \sim \chi_{m(n-1)}^2</math>, | ||
| + | </center> | ||
| + | |||
| + | and | ||
| + | |||
| + | <center> | ||
| + | <math>\frac{SS_b}{\sigma^2} \sim \chi_{m-1}^2</math>. | ||
| + | </center> | ||
| + | |||
| + | Also, since <math>S_i^2</math> is independent of <math>\bar{X}_{i\centerdot}</math>, <math>SS_w</math> and <math>SS_b</math> are independent. Thus, the statistic | ||
| + | |||
| + | <center> | ||
| + | <math> | ||
| + | \frac{SS_b/(m-1)}{SS_w/m(n-1)} \sim F_{m-1,m(n-1)}. | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | Therefore, we can use the table for the F-distribution to test for <math>H_0</math>. | ||
รุ่นแก้ไขปัจจุบันเมื่อ 03:00, 4 ธันวาคม 2557
- This is part of probstat.
Data generation
Generate 5 sets of samples from normal populations, each of size 10, on a spreadsheet software. Make sure that the mean and variance of each set can be modified easily.
Variance estimations
Estimator 1. The first estimator for is
This estimator is always correct. (Even when is not true.)
Estimator 2. The second estimator is calculated from the sample means. It will be correct only when is true.
Hypothesis testing
Then compute
and
Recall that
,
and
.
Also, since is independent of , and are independent. Thus, the statistic
Therefore, we can use the table for the F-distribution to test for .