ผลต่างระหว่างรุ่นของ "VC-SNDP:spider decomposition"
Top (คุย | มีส่วนร่วม) |
Top (คุย | มีส่วนร่วม) |
||
| แถว 18: | แถว 18: | ||
[[ภาพ:Spiders.png]] | [[ภาพ:Spiders.png]] | ||
| − | ===พิสูจน์=== | + | ===พิสูจน์=== โดย induction บนจำนวน edge ระหว่าง white vertices ใน G |
| + | ใน base case ให้กราฟ G ไม่มี edge ดังกล่าวเลย จะได้ว่า G เป็น bipartite. ( edge ระหว่าง black vertices ก็ไม่มีด้วย) | ||
| + | เนื่องจากแต่ละคู่ของ black vertices เป็น k-element connected แสดงว่าแต่ละ black vertex จะต้องมีอย่างน้อย k white vertices ที่ติดกับมัน | ||
| + | |||
| + | เราจะสร้าง set of spiders โดยให้แต่ละโหนด b | ||
== Approximating SS-k-VC-SNDP == | == Approximating SS-k-VC-SNDP == | ||
รุ่นแก้ไขเมื่อ 06:05, 25 กุมภาพันธ์ 2552
This page describes spider decompositions and the approach of Chuzhoy Khanna and Chekuri and Korula in tackling the single-source k sndp.
ให้กราฟ เซตของ terminals T และจำนวนเต็มบวก เรียกโหนดใน T ว่าเป็น black vertices, นอกจากนั้นเป็น white vertices.
Spider คือ tree ที่มีโหนดที่มีดีกรีมากกว่าสองไม่เกิน 1 จุดยอด ถ้ามี vertex ดังกล่าว จะเรียกว่าเป็น head ถ้าไม่มี spider จะเป็น path และจะสามารถเรียกโหนดใดเป็น head ก็ได้; เรียกจุดยอดที่ไม่ใช่ leaf และ head ว่า intermediate vertex, เรียก leaf ว่า foot, เรียก path จาก head ไป leaf ว่า leg
เนื้อหา
Decomposition
Chuzhoy และ Khanna ได้ใช้ spider decomposition ในการพิสูจน์ approximation algorithm สำหรับ ss-k-sndp อย่างไรก็ตามในที่นี้เราจะใช้ decomposition ที่ weak กว่าของ Chekuri และ Korula
Chekuri-Korula [Theorem 4.4] แสดงว่า ให้กราฟ G ที่ทุก ๆ คู่ของจุดยอดสีดำ k-element connected, มีสับกราฟ H ของ G ที่สามารถ partition เป็น spiders ที่
- ทุก ๆ leaf เป็น black vertex
- ทุก ๆ black vertex เป็น foot ของ k spiders พอดี
- ทุก ๆ intermediate vertex เป็น white vertex (สังเกตว่า head เป็น black vertex ได้) และสำหรับกรณีที่ spider มี white vertex เป็น head จะต้องมี leg อย่างน้อย 2 legs
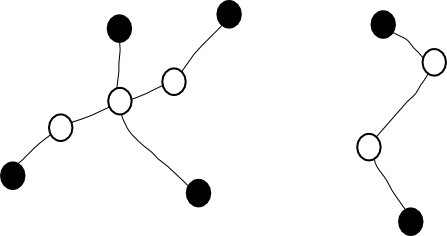
ด้านล่างแสดงตัวอย่างของ spiders
===พิสูจน์=== โดย induction บนจำนวน edge ระหว่าง white vertices ใน G ใน base case ให้กราฟ G ไม่มี edge ดังกล่าวเลย จะได้ว่า G เป็น bipartite. ( edge ระหว่าง black vertices ก็ไม่มีด้วย) เนื่องจากแต่ละคู่ของ black vertices เป็น k-element connected แสดงว่าแต่ละ black vertex จะต้องมีอย่างน้อย k white vertices ที่ติดกับมัน
เราจะสร้าง set of spiders โดยให้แต่ละโหนด b