ผลต่างระหว่างรุ่นของ "VC-SNDP:spider decomposition"
Jittat (คุย | มีส่วนร่วม) |
Jittat (คุย | มีส่วนร่วม) |
||
| (ไม่แสดง 34 รุ่นระหว่างกลางโดยผู้ใช้ 2 คน) | |||
| แถว 4: | แถว 4: | ||
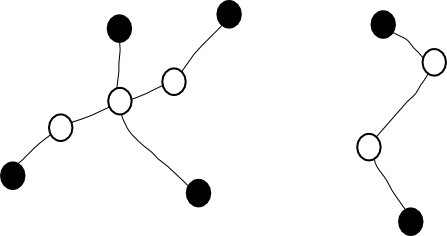
'''Spider''' คือ tree ที่มีโหนดที่มีดีกรีมากกว่าสองไม่เกิน 1 จุดยอด ถ้ามี vertex ดังกล่าว จะเรียกว่าเป็น '''head''' ถ้าไม่มี spider จะเป็น path และจะสามารถเรียกโหนดใดเป็น head ก็ได้; เรียกจุดยอดที่ไม่ใช่ leaf และ head ว่า '''intermediate vertex''', เรียก leaf ว่า '''foot''', เรียก path จาก head ไป leaf ว่า '''leg''' | '''Spider''' คือ tree ที่มีโหนดที่มีดีกรีมากกว่าสองไม่เกิน 1 จุดยอด ถ้ามี vertex ดังกล่าว จะเรียกว่าเป็น '''head''' ถ้าไม่มี spider จะเป็น path และจะสามารถเรียกโหนดใดเป็น head ก็ได้; เรียกจุดยอดที่ไม่ใช่ leaf และ head ว่า '''intermediate vertex''', เรียก leaf ว่า '''foot''', เรียก path จาก head ไป leaf ว่า '''leg''' | ||
| + | |||
| + | === ภาพรวม (ตาม Chekuri-Korula) === | ||
| + | * อัลกอริทึมใช้ greedy augmentation บนลำดับแบบสุ่มของ terminal | ||
| + | * cost พิสูจน์ด้วย '''Theorem 4.2''' ที่แสดงว่า cost ในการทำ augmentation '''จากทุกโหนด''' ไม่เกิน <math>8k\cdot OPT</math> (ดูด้านล่าง) | ||
| + | * key lemma คือ '''Lemma 4.3''' ที่แสดงว่ามีจากทุก ๆ terminal มี set ของ internal vertex disjoint path ไปยัง terminal อื่น ๆ ที่ cost รวมไม่เกิน 2 เท่าของ opt, lemma นี้พิสูจน์ได้โดยแสดงว่ามี spider decomposition | ||
| + | * spider decomposition พิสูจน์ด้วย Reduction Lemma | ||
| + | |||
| + | '''ข้อสังเกต''': จาก Lemma 4.3 มา Theorem 4.2 เสียไป <math>k</math> | ||
== Decomposition == | == Decomposition == | ||
| แถว 11: | แถว 19: | ||
Chekuri-Korula [Theorem 4.4] แสดงว่า ให้กราฟ G ที่ทุก ๆ คู่ของจุดยอดสีดำ ''k''-element connected, มีสับกราฟ ''H'' ของ ''G'' ที่สามารถ partition เป็น spiders ที่ | Chekuri-Korula [Theorem 4.4] แสดงว่า ให้กราฟ G ที่ทุก ๆ คู่ของจุดยอดสีดำ ''k''-element connected, มีสับกราฟ ''H'' ของ ''G'' ที่สามารถ partition เป็น spiders ที่ | ||
# ทุก ๆ leaf เป็น black vertex และ ทุก ๆ intermediate vertex เป็น white vertex (สังเกตว่า head เป็น black vertex ได้) | # ทุก ๆ leaf เป็น black vertex และ ทุก ๆ intermediate vertex เป็น white vertex (สังเกตว่า head เป็น black vertex ได้) | ||
| − | # ทุก ๆ black vertex เป็น foot ของ ''k'' spiders พอดี, และ ทุก ๆ white vertex อยู่ใน 1 spider เท่านั้น | + | # ทุก ๆ black vertex เป็น '''foot ของ ''k'' spiders พอดี''', และ ทุก ๆ white vertex '''อยู่ใน 1 spider เท่านั้น''' |
# สำหรับกรณีที่ spider มี white vertex เป็น head จะต้องมี leg อย่างน้อย 2 legs | # สำหรับกรณีที่ spider มี white vertex เป็น head จะต้องมี leg อย่างน้อย 2 legs | ||
| แถว 19: | แถว 27: | ||
===spider decomposition กับ set ของ paths=== | ===spider decomposition กับ set ของ paths=== | ||
| + | พิจารณา spider แต่ละตัว เราจะพบว่าเราสามารถหาเซตของ path จากแต่ละ foot หนึ่ง ๆ ไปยังอีก foot ใด ๆ ได้ โดยที่ค่าใช้จ่ายรวมไม่เกิน 2 เท่าของ cost ของ spider (ดูรูป) | ||
| + | |||
| + | [[ภาพ:Spiders-paths.png]] | ||
| + | |||
| + | ดังนั้น ถ้าเรามี spider decomposition เราจะได้ว่าเราสามารถหา, สำหรับทุก ๆ terminal <math>t</math>, set of <math>k</math> internally vertex disjoint paths <math>{\mathcal P}_t</math> ที่ <math>\sum_{t\in T}cost({\mathcal P}_t)\leq 2\cdot(\mbox{cost of all spiders})</math> เพราะว่า | ||
| + | |||
| + | * สังเกตว่า white vertex ไม่ share กันระหว่าง spider | ||
| + | * ทุก ๆ black vertex เป็น leg ของ ''k'' spiders (ดังนั้นดึงมาตัวละ path) | ||
| + | |||
| + | ด้านบนคือหัวใจของบทพิสูจน์ของ Lemma 4.3 ใน Chekuri-Korula | ||
| + | |||
| + | ===Spider decomposition บนกรณี bipartite=== | ||
| + | พิจารณากรณีที่ไม่มีเส้นเชื่อมระหว่าง 2 white vertices เราสามารถสมมติว่าไม่มีเส้นเชื่อมระหว่าง black vertices ได้ด้วย โดยการใส่จุดขาวลงไปตรงกลางเส้นเชื่อมระหว่าง black vertices ดังนั้นเราอยู่ในกรณีที่กราฟเป็น bipartite โดยกลุ่มหนึ่งคือ white vertices อีกกลุ่มคือ black vertices | ||
| + | |||
| + | เราจะแสดงว่า ในกรณี bipartite ดังกล่าว บนกราฟที่ทุก ๆ terminal นั้น <math>k</math>-vertex connected ไปยัง root จะมี spider decomposition | ||
| + | |||
| + | * ก่อนอื่น สังเกตว่า เราสามารถลบ white vertex ที่มี degree เป็น 1 ทิ้งได้ (เพราะว่าไม่ได้ทำให้ terminal ใดติดกับใครได้เลย) | ||
| + | * จากนั้น สังเกตว่าทุก ๆ terminal <math>u</math> จะต้องมี อย่างน้อย <math>k</math> vertices ที่ติดกับมัน และจะต้องเป็น white vertices ทั้งหมดด้วย | ||
| + | * เลือก edge ที่ติดกับ <math>u</math> มา <math>k</math> edges | ||
| + | * พิจารณา white vertex <math>v</math> ที่มีบาง edge ที่ติดกับมันโดนเลือก | ||
| + | ** ถ้ามีอย่างน้อย 2 edge --- ให้ vertex นั้นเป็น head ของ spider และให้แต่ละ terminal ที่เลือก edge เหล่านั้นเป็น foot ของ spider | ||
| + | ** ถ้ามีแค่ edge เดียว --- ให้เลือก edge ที่ติดกับ <math>v</math> ไปยัง อีก terminal หนึ่ง สมมติว่าเป็น <math>w</math>, ให้ <math>w</math> เป็น head ของ spider ที่มี <math>u</math> เป็น foot | ||
| + | |||
| + | พิจารณารูปด้านล่าง (กรณี k=2) รูปซ้ายแสดงการเลือก เส้นเชื่อมสีเขียวคือเส้นเชื่อมที่ไม่ถูกเลือก รูปขวาแสดง spider 2 spider, สังเกตว่า black vertex ที่สามจากซ้าย เป็น foot ของ 2 spiders และเป็น head ของอีก 1 spider | ||
| + | |||
| + | [[ภาพ:Spider-bipartite.png]] | ||
| + | |||
| + | ===บทพิสูจน์: มี spider decomposition (Thm 4.4 ใน Chekuri-Korula)=== | ||
| + | |||
| + | ส่วนนี้จะมาเขียนทีหลัง | ||
| − | |||
โดย induction บนจำนวน edge ระหว่าง white vertices ใน G | โดย induction บนจำนวน edge ระหว่าง white vertices ใน G | ||
ใน base case ให้กราฟ G ไม่มี edge ดังกล่าวเลย จะได้ว่า G เป็น bipartite. ( edge ระหว่าง black vertices ก็ไม่มีด้วย) | ใน base case ให้กราฟ G ไม่มี edge ดังกล่าวเลย จะได้ว่า G เป็น bipartite. ( edge ระหว่าง black vertices ก็ไม่มีด้วย) | ||
| แถว 28: | แถว 65: | ||
== Approximating SS-k-VC-SNDP == | == Approximating SS-k-VC-SNDP == | ||
| + | ในส่วนนี้จะอธิบายอัลกอริทึมตามที่ปรากฎใน Chekuri-Korula | ||
| + | |||
| + | ให้กราฟ <math>G=(V,E)</math> เซตของ terminals <math>T</math> และ root <math>r</math> | ||
| + | |||
| + | สำหรับสับเซตของ terminals <math>T'</math> ใด ๆ และ terminal <math>t\in T-T'</math>, เราจะกล่าวว่า เซตของ <math>k</math> paths <math>p_1,p_2,\ldots,p_k</math> เป็น '''augmentation for <math>t</math> w.r.t. <math>T'</math>''' ถ้า | ||
| + | |||
| + | * path เริ่มที่ ''t'' ไปถึงโหนดใน <math>T'\cup\{r\}</math> | ||
| + | * path เหล่านั้น internally vertex disjoint, | ||
| + | * terminal ใน <math>T'</math> เป็นจุดปลายได้แค่ path เดียว | ||
| + | |||
| + | อัลกอริทึมเป็นดังนี้ | ||
| + | |||
| + | 1. สุ่มลำดับ terminal ให้เป็น <math>t_1,t_2,\ldots,t_j</math> | ||
| + | 2. ให้ ''H'' เป็นกราฟว่าง | ||
| + | 3. พิจารณา <math>t=t_1,t_2,\ldots</math> | ||
| + | 3.1 หา min-cost augmentation for <math>t</math> w.r.t. <math>T_{i-1}</math> เมื่อ <math>T_i=\{t_1,\ldots,t_i\}</math> | ||
| + | 3.2 นำผลลัพธ์ที่ได้ใส่ใน ''H'' | ||
| + | 4. output ''H'' | ||
| + | |||
| + | === ความถูกต้อง === | ||
| + | |||
| + | เก็บไว้เป็นการบ้านก่อนแล้วกันนะ ;) | ||
| + | |||
| + | === ค่าใช้จ่าย === | ||
| + | key หลักในการพิสูจน์เกี่ยวกับค่าใช้จ่ายคือ Theorem 4.2 ดังแสดงด้านล่าง | ||
| + | |||
| + | {{กล่องสี|#ddddff| | ||
| + | '''Theorem 4.2''' ให้ ''OPT'' แทนค่าใช้จ่ายของ optimal solution, และ <math>AugCost(t)</math> แทนค่าใช้จ่ายในการ augmentation for ''t'' w.r.t <math>T-\{t\}</math>, <math>\sum_{t} AugCost(t)\leq 8k\cdot OPT</math> | ||
| + | }} | ||
| + | |||
| + | จาก theorem ดังกล่าว เราจะพิสูจน์ว่าอัลกอริทึมด้านบนมี expected cost <math>O(k\cdot\log|T|\cdot OPT)</math> | ||
| + | |||
| + | {{กล่องสี|#ddffdd| | ||
| + | '''Claim:''' Expected cost ในการ augment <math>t_i</math> คือ <math>8k\cdot OPT/i</math> | ||
| + | }} | ||
| + | |||
| + | '''Proof of claim:''' (sketch) สำหรับ <math>T'\subseteq T</math>, ให้ <math>OPT(T')</math> แทนคำตอบที่ดีที่สุดของ SS-k-SNDP เมื่อให้ terminal set เป็น <math>T'</math> | ||
| + | |||
| + | * <math>OPT(T')\leq OPT(T)</math> | ||
| + | * ใช้ Theorem 4.2 บน <math>T_i</math> จะได้ว่า <math>\sum_{t\in T_i} AugCost(t)\leq 8k\cdot OPT(T_i)\leq 8k\cdot OPT(T)</math> | ||
| + | * สังเกตว่า given <math>T_i</math> โหนดสุดท้ายที่จะถูก add (นั่นคือ <math>t_i</math>) สามารถเป็นโหนดใด ๆ ก็ได้ใน <math>T_i</math> ดังนั้น expected cost คือ <math>8k\cdot OPT/i</math> ตามต้องการ เพราะ <math>|T_i|=i</math> | ||
| + | |||
| + | จาก claim ดังกล่าว approximation ratio สามารถพิสูจน์ได้โดยใช้ linearity of expectation. | ||
| + | |||
| + | *note ถ้าไม่สุ่ม permutation แล้วคิดแบบ expected จะมีกรณีที่อัลกอริทึมให้ผลลัพธ์ที่มีค่าใช้จ่ายเป็น <math>\Omega (|T|\cdot OPT)</math> | ||
== Reduction lemma == | == Reduction lemma == | ||
=== Proof of the spider decomposition with the reduction lemma === | === Proof of the spider decomposition with the reduction lemma === | ||
รุ่นแก้ไขปัจจุบันเมื่อ 17:18, 27 กุมภาพันธ์ 2552
This page describes spider decompositions and the approach of Chuzhoy Khanna and Chekuri and Korula in tackling the single-source k sndp.
ให้กราฟ เซตของ terminals T และจำนวนเต็มบวก เรียกโหนดใน T ว่าเป็น black vertices, นอกจากนั้นเป็น white vertices.
Spider คือ tree ที่มีโหนดที่มีดีกรีมากกว่าสองไม่เกิน 1 จุดยอด ถ้ามี vertex ดังกล่าว จะเรียกว่าเป็น head ถ้าไม่มี spider จะเป็น path และจะสามารถเรียกโหนดใดเป็น head ก็ได้; เรียกจุดยอดที่ไม่ใช่ leaf และ head ว่า intermediate vertex, เรียก leaf ว่า foot, เรียก path จาก head ไป leaf ว่า leg
เนื้อหา
ภาพรวม (ตาม Chekuri-Korula)
- อัลกอริทึมใช้ greedy augmentation บนลำดับแบบสุ่มของ terminal
- cost พิสูจน์ด้วย Theorem 4.2 ที่แสดงว่า cost ในการทำ augmentation จากทุกโหนด ไม่เกิน (ดูด้านล่าง)
- key lemma คือ Lemma 4.3 ที่แสดงว่ามีจากทุก ๆ terminal มี set ของ internal vertex disjoint path ไปยัง terminal อื่น ๆ ที่ cost รวมไม่เกิน 2 เท่าของ opt, lemma นี้พิสูจน์ได้โดยแสดงว่ามี spider decomposition
- spider decomposition พิสูจน์ด้วย Reduction Lemma
ข้อสังเกต: จาก Lemma 4.3 มา Theorem 4.2 เสียไป
Decomposition
Chuzhoy และ Khanna ได้ใช้ spider decomposition ในการพิสูจน์ approximation algorithm สำหรับ ss-k-sndp อย่างไรก็ตามในที่นี้เราจะใช้ decomposition ที่ weak กว่าของ Chekuri และ Korula
Chekuri-Korula [Theorem 4.4] แสดงว่า ให้กราฟ G ที่ทุก ๆ คู่ของจุดยอดสีดำ k-element connected, มีสับกราฟ H ของ G ที่สามารถ partition เป็น spiders ที่
- ทุก ๆ leaf เป็น black vertex และ ทุก ๆ intermediate vertex เป็น white vertex (สังเกตว่า head เป็น black vertex ได้)
- ทุก ๆ black vertex เป็น foot ของ k spiders พอดี, และ ทุก ๆ white vertex อยู่ใน 1 spider เท่านั้น
- สำหรับกรณีที่ spider มี white vertex เป็น head จะต้องมี leg อย่างน้อย 2 legs
ด้านล่างแสดงตัวอย่างของ spiders
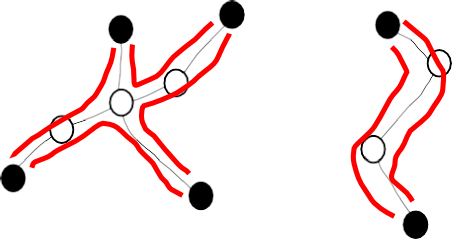
spider decomposition กับ set ของ paths
พิจารณา spider แต่ละตัว เราจะพบว่าเราสามารถหาเซตของ path จากแต่ละ foot หนึ่ง ๆ ไปยังอีก foot ใด ๆ ได้ โดยที่ค่าใช้จ่ายรวมไม่เกิน 2 เท่าของ cost ของ spider (ดูรูป)
ดังนั้น ถ้าเรามี spider decomposition เราจะได้ว่าเราสามารถหา, สำหรับทุก ๆ terminal , set of internally vertex disjoint paths ที่ เพราะว่า
- สังเกตว่า white vertex ไม่ share กันระหว่าง spider
- ทุก ๆ black vertex เป็น leg ของ k spiders (ดังนั้นดึงมาตัวละ path)
ด้านบนคือหัวใจของบทพิสูจน์ของ Lemma 4.3 ใน Chekuri-Korula
Spider decomposition บนกรณี bipartite
พิจารณากรณีที่ไม่มีเส้นเชื่อมระหว่าง 2 white vertices เราสามารถสมมติว่าไม่มีเส้นเชื่อมระหว่าง black vertices ได้ด้วย โดยการใส่จุดขาวลงไปตรงกลางเส้นเชื่อมระหว่าง black vertices ดังนั้นเราอยู่ในกรณีที่กราฟเป็น bipartite โดยกลุ่มหนึ่งคือ white vertices อีกกลุ่มคือ black vertices
เราจะแสดงว่า ในกรณี bipartite ดังกล่าว บนกราฟที่ทุก ๆ terminal นั้น -vertex connected ไปยัง root จะมี spider decomposition
- ก่อนอื่น สังเกตว่า เราสามารถลบ white vertex ที่มี degree เป็น 1 ทิ้งได้ (เพราะว่าไม่ได้ทำให้ terminal ใดติดกับใครได้เลย)
- จากนั้น สังเกตว่าทุก ๆ terminal จะต้องมี อย่างน้อย vertices ที่ติดกับมัน และจะต้องเป็น white vertices ทั้งหมดด้วย
- เลือก edge ที่ติดกับ มา edges
- พิจารณา white vertex ที่มีบาง edge ที่ติดกับมันโดนเลือก
- ถ้ามีอย่างน้อย 2 edge --- ให้ vertex นั้นเป็น head ของ spider และให้แต่ละ terminal ที่เลือก edge เหล่านั้นเป็น foot ของ spider
- ถ้ามีแค่ edge เดียว --- ให้เลือก edge ที่ติดกับ ไปยัง อีก terminal หนึ่ง สมมติว่าเป็น , ให้ เป็น head ของ spider ที่มี เป็น foot
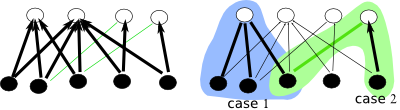
พิจารณารูปด้านล่าง (กรณี k=2) รูปซ้ายแสดงการเลือก เส้นเชื่อมสีเขียวคือเส้นเชื่อมที่ไม่ถูกเลือก รูปขวาแสดง spider 2 spider, สังเกตว่า black vertex ที่สามจากซ้าย เป็น foot ของ 2 spiders และเป็น head ของอีก 1 spider
บทพิสูจน์: มี spider decomposition (Thm 4.4 ใน Chekuri-Korula)
ส่วนนี้จะมาเขียนทีหลัง
โดย induction บนจำนวน edge ระหว่าง white vertices ใน G ใน base case ให้กราฟ G ไม่มี edge ดังกล่าวเลย จะได้ว่า G เป็น bipartite. ( edge ระหว่าง black vertices ก็ไม่มีด้วย) เนื่องจากแต่ละคู่ของ black vertices เป็น k-element connected แสดงว่าแต่ละ black vertex จะต้องมีอย่างน้อย k white vertices ที่ติดกับมัน
เราจะสร้าง set of spiders โดยให้แต่ละโหนด b
Approximating SS-k-VC-SNDP
ในส่วนนี้จะอธิบายอัลกอริทึมตามที่ปรากฎใน Chekuri-Korula
ให้กราฟ เซตของ terminals และ root
สำหรับสับเซตของ terminals ใด ๆ และ terminal , เราจะกล่าวว่า เซตของ paths เป็น augmentation for w.r.t. ถ้า
- path เริ่มที่ t ไปถึงโหนดใน
- path เหล่านั้น internally vertex disjoint,
- terminal ใน เป็นจุดปลายได้แค่ path เดียว
อัลกอริทึมเป็นดังนี้
1. สุ่มลำดับ terminal ให้เป็น 2. ให้ H เป็นกราฟว่าง 3. พิจารณา 3.1 หา min-cost augmentation for w.r.t. เมื่อ 3.2 นำผลลัพธ์ที่ได้ใส่ใน H 4. output H
ความถูกต้อง
เก็บไว้เป็นการบ้านก่อนแล้วกันนะ ;)
ค่าใช้จ่าย
key หลักในการพิสูจน์เกี่ยวกับค่าใช้จ่ายคือ Theorem 4.2 ดังแสดงด้านล่าง
Theorem 4.2 ให้ OPT แทนค่าใช้จ่ายของ optimal solution, และ แทนค่าใช้จ่ายในการ augmentation for t w.r.t ,
จาก theorem ดังกล่าว เราจะพิสูจน์ว่าอัลกอริทึมด้านบนมี expected cost
Claim: Expected cost ในการ augment คือ
Proof of claim: (sketch) สำหรับ , ให้ แทนคำตอบที่ดีที่สุดของ SS-k-SNDP เมื่อให้ terminal set เป็น
- ใช้ Theorem 4.2 บน จะได้ว่า
- สังเกตว่า given โหนดสุดท้ายที่จะถูก add (นั่นคือ ) สามารถเป็นโหนดใด ๆ ก็ได้ใน ดังนั้น expected cost คือ ตามต้องการ เพราะ
จาก claim ดังกล่าว approximation ratio สามารถพิสูจน์ได้โดยใช้ linearity of expectation.
- note ถ้าไม่สุ่ม permutation แล้วคิดแบบ expected จะมีกรณีที่อัลกอริทึมให้ผลลัพธ์ที่มีค่าใช้จ่ายเป็น