ผลต่างระหว่างรุ่นของ "คณิตศาสตร์แบบเวคเตอร์ใน VPython"
Chaiporn (คุย | มีส่วนร่วม) |
Chaiporn (คุย | มีส่วนร่วม) |
||
| แถว 59: | แถว 59: | ||
[[Image:vpython-vec-mul-div.png|center|600px]] | [[Image:vpython-vec-mul-div.png|center|600px]] | ||
| + | |||
| + | == ขนาดของเวกเตอร์ == | ||
| + | เวกเตอร์ 2 มิติ <math>\mathbf{v} = \begin{bmatrix}x\\y\end{bmatrix}</math> มีขนาด (หรือความยาว) ตามทฤษฎีของปีทาโกรัสดังนี้ | ||
| + | |||
| + | :<math>||\mathbf{v}|| = \sqrt{x^2+y^2}</math> | ||
| + | |||
| + | ขนาดของเวกเตอร์คำนวณได้จากฟังก์ชัน <tt>mag()</tt> ในโมดูล visual ดังตัวอย่าง | ||
| + | |||
| + | >>> from visual import vector,mag | ||
| + | >>> v = vector(3,4) | ||
| + | >>> print(mag(v)) | ||
| + | 5.0 | ||
| + | |||
| + | ดังนั้นสำหรับเวกเตอร์ใด ๆ ที่ขนาดไม่เป็นศูนย์ เราสามารถสร้างเวกเตอร์หนึ่งหน่วยที่ชี้ไปทางเดียวกับเวกเตอร์นั้น โดยการหารเวกเตอร์นั้นด้วยขนาดของตัวเอง ดังตัวอย่าง | ||
| + | |||
| + | >>> u = v/mag(v) | ||
| + | >>> print(u) | ||
| + | <0.6, 0.8, 0> | ||
| + | >>> print(mag(u)) | ||
| + | 1.0 | ||
รุ่นแก้ไขเมื่อ 14:53, 10 ตุลาคม 2558
- วิกินี้เป็นส่วนหนึ่งของรายวิชา 01204223
- เนื้อหาในวิกินี้ดัดแปลงมาจากกิจกรรมประกอบหนังสือเรียนรายวิชาเพิ่มเติม เทคโนโลยีสารสนเทศและการสื่อสาร ภาษาไพทอน โดยสถาบันส่งเสริมการสอนวิทยาศาสตร์และเทคโนโลยี
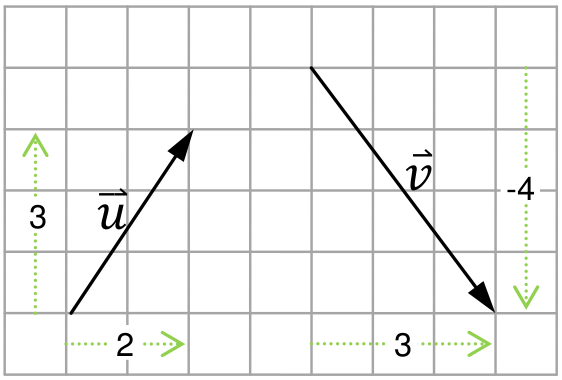
โมดูล visual ในไลบรารี VPython รองรับการประมวลผลทางคณิตศาสตร์เชิงเวคเตอร์โดยเตรียมคลาสชื่อ vector เพื่อใช้สร้างปริมาณเวกเตอร์ตั้งแต่หนึ่งถึงสามมิติ ตัวอย่างต่อไปนี้เป็นการนิยามเวกเตอร์ และเวกเตอร์ ไว้ในตัวแปร u และ v ตามลำดับ
>>> from visual import vector >>> u = vector(2,3) >>> v = vector(3,-4) >>> print(u,v) <2, 3, 0> <3, -4, 0>
จะเห็นว่าเวกเตอร์ที่สร้างขึ้นมีขนาด 3 มิติ อย่างไรก็ตามกิจกรรมนี้จะสนใจเพียงสองมิติแรก ซึ่งหากไม่สนใจมิติที่สามแล้วค่าของ u และ v ข้างต้นจะสอดคล้องกับแผนภาพดังนี้
ปริมาณในแต่ละมิติของเวกเตอร์สามารถอ้างถึงผ่านคุณลักษณะชื่อ x และ y ของเวกเตอร์นั้น ๆ และยังอ้างอิงตามรูปแบบลิสต์ได้เช่นกัน ตัวอย่างเช่น
>>> v = vector(2,3) >>> print(v.x,v.y) 2.0 3.0 >>> print(v[0],v[1]) 2.0 3.0 >>> v.x = -8.5 >>> print(v) <-8.5, 3, 0>
การบวกและลบเวกเตอร์
เนื่องจากภาษาไพทอนรองรับการทำ Operator Overloading ข้อมูลชนิดเวกเตอร์ที่สร้างขึ้นจากคลาส vector ของ VPython สามารถนำมาประมวลผลด้วยตัวดำเนินการทางคณิตศาสตร์ + และ – ได้ทันที ดังตัวอย่าง
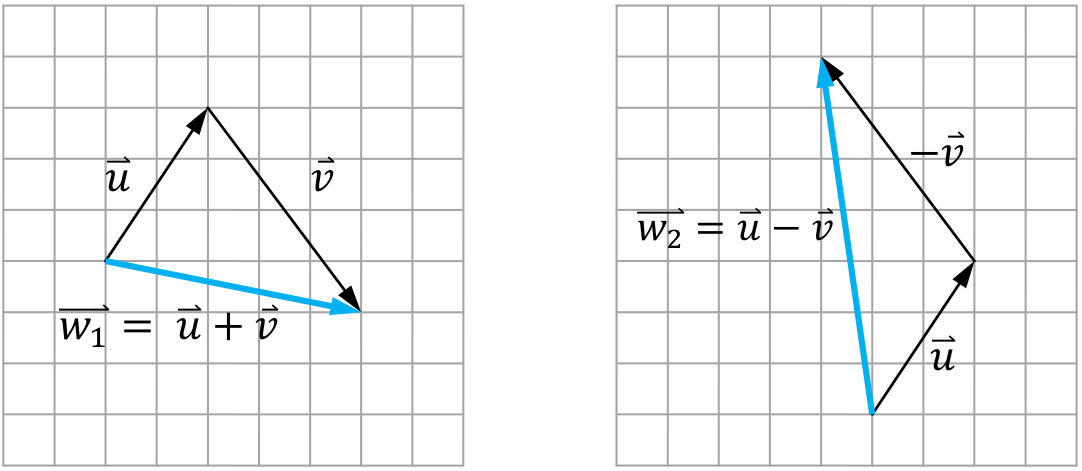
>>> from visual import vector >>> u = vector(2,3) >>> v = vector(3,-4) >>> w1 = u+v >>> w2 = u-v >>> print(w1,w2) <5, -1, 0> <-1, 7, 0>
ซึ่งสอดคล้องกับแผนภาพ
การคูณและหารเวกเตอร์ด้วยสเกลาร์
ปริมาณเวกเตอร์ที่สร้างขึ้นสามารถนำมาคูณหรือหารด้วยปริมาณสเกลาร์ผ่านตัวดำเนินการ * และ /
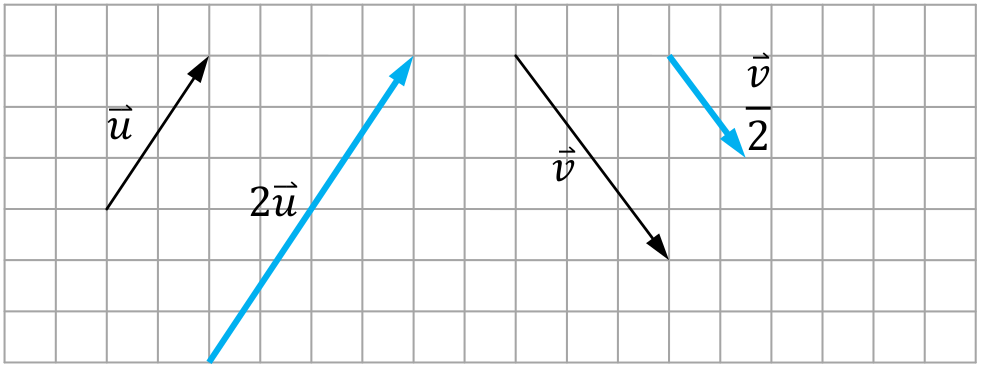
>>> w3 = u*2 >>> w4 = v/2 >>> print(w3) <4, 6, 0> >>> print(w4) <1.5, -2, 0>
ซึ่งให้ผลลัพธ์เป็นเวกเตอร์ใหม่ที่ขนาดเปลี่ยนไปแต่ยังคงทิศทางเดิม ดังแผนภาพ
ขนาดของเวกเตอร์
เวกเตอร์ 2 มิติ มีขนาด (หรือความยาว) ตามทฤษฎีของปีทาโกรัสดังนี้
ขนาดของเวกเตอร์คำนวณได้จากฟังก์ชัน mag() ในโมดูล visual ดังตัวอย่าง
>>> from visual import vector,mag >>> v = vector(3,4) >>> print(mag(v)) 5.0
ดังนั้นสำหรับเวกเตอร์ใด ๆ ที่ขนาดไม่เป็นศูนย์ เราสามารถสร้างเวกเตอร์หนึ่งหน่วยที่ชี้ไปทางเดียวกับเวกเตอร์นั้น โดยการหารเวกเตอร์นั้นด้วยขนาดของตัวเอง ดังตัวอย่าง
>>> u = v/mag(v) >>> print(u) <0.6, 0.8, 0> >>> print(mag(u)) 1.0