ผลต่างระหว่างรุ่นของ "จำลองการเคลื่อนที่ด้วยคณิตศาสตร์แบบเวกเตอร์ใน VPython"
Chaiporn (คุย | มีส่วนร่วม) |
Chaiporn (คุย | มีส่วนร่วม) |
||
| (ไม่แสดง 2 รุ่นระหว่างกลางโดยผู้ใช้คนเดียวกัน) | |||
| แถว 66: | แถว 66: | ||
:<math>||\mathbf{v}|| = \sqrt{x^2+y^2}</math> | :<math>||\mathbf{v}|| = \sqrt{x^2+y^2}</math> | ||
| − | + | ขนาดของเวกเตอร์คำนวณได้จากคุณสมบัติ <tt>mag</tt> ดังตัวอย่าง | |
| − | >>> from vis import vector | + | >>> from vis import vector |
>>> v = vector(3,4) | >>> v = vector(3,4) | ||
| − | >>> print mag | + | >>> print v.mag |
5.0 | 5.0 | ||
ดังนั้นสำหรับเวกเตอร์ใด ๆ ที่ขนาดไม่เป็นศูนย์ เราสามารถสร้างเวกเตอร์หนึ่งหน่วยที่ชี้ไปทางเดียวกับเวกเตอร์นั้น โดยการหารเวกเตอร์นั้นด้วยขนาดของมันเอง ดังตัวอย่าง | ดังนั้นสำหรับเวกเตอร์ใด ๆ ที่ขนาดไม่เป็นศูนย์ เราสามารถสร้างเวกเตอร์หนึ่งหน่วยที่ชี้ไปทางเดียวกับเวกเตอร์นั้น โดยการหารเวกเตอร์นั้นด้วยขนาดของมันเอง ดังตัวอย่าง | ||
| − | >>> u = v/mag | + | >>> u = v/v.mag |
| − | >>> print | + | >>> print u |
<0.6, 0.8, 0> | <0.6, 0.8, 0> | ||
| − | >>> print mag | + | >>> print u.mag |
1.0 | 1.0 | ||
| แถว 89: | แถว 89: | ||
:<math>\mathbf{s}(t+\Delta t) = \mathbf{s}(t) + \mathbf{v}(t)\Delta t</math> | :<math>\mathbf{s}(t+\Delta t) = \mathbf{s}(t) + \mathbf{v}(t)\Delta t</math> | ||
| + | |||
| + | ซึ่งมีความหมายว่าเราสามารถทราบตำแหน่งของวัตถุหลังจากที่เวลาผ่านไป <math>\Delta t</math> ได้โดยอาศัยความเร็วและตำแหน่งปัจจุบันของมัน | ||
ในทำนองเดียวกัน ความสัมพันธ์ระหว่างความเร่ง <math>\mathbf{a}(t)</math> และความเร็ว <math>\mathbf{v}(t)</math> สามารถเขียนในรูป | ในทำนองเดียวกัน ความสัมพันธ์ระหว่างความเร่ง <math>\mathbf{a}(t)</math> และความเร็ว <math>\mathbf{v}(t)</math> สามารถเขียนในรูป | ||
| แถว 104: | แถว 106: | ||
scene.range = 100 # กำหนดช่องหน้าต่างแสดงผลให้ครอบคลุมรัศมี 100 หน่วยจากศูนย์กลางจอ | scene.range = 100 # กำหนดช่องหน้าต่างแสดงผลให้ครอบคลุมรัศมี 100 หน่วยจากศูนย์กลางจอ | ||
| − | # สร้างลูกบอลสีเหลืองรัศมี 5 หน่วยไว้ที่พิกัด ( | + | # สร้างลูกบอลสีเหลืองรัศมี 5 หน่วยไว้ที่พิกัด (-50,-50) |
ball = vis.sphere(pos=(-50,-50),radius=5,color=vis.color.yellow,make_trail=True) | ball = vis.sphere(pos=(-50,-50),radius=5,color=vis.color.yellow,make_trail=True) | ||
รุ่นแก้ไขปัจจุบันเมื่อ 10:25, 19 ตุลาคม 2558
- วิกินี้เป็นส่วนหนึ่งของรายวิชา 01204223
- เนื้อหาในวิกินี้ดัดแปลงมาจากกิจกรรมประกอบหนังสือเรียนรายวิชาเพิ่มเติม เทคโนโลยีสารสนเทศและการสื่อสาร ภาษาไพทอน โดยสถาบันส่งเสริมการสอนวิทยาศาสตร์และเทคโนโลยี
เนื้อหา
คลาส vector ใน VPython
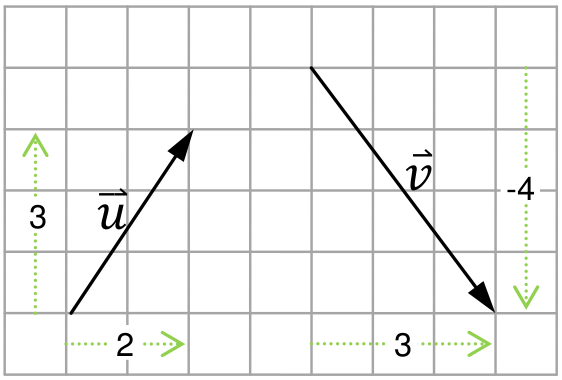
โมดูล visual และ vis ในไลบรารี VPython รองรับการประมวลผลทางคณิตศาสตร์เชิงเวกเตอร์โดยเตรียมคลาสชื่อ vector เพื่อใช้สร้างปริมาณเวกเตอร์ตั้งแต่หนึ่งถึงสามมิติ ตัวอย่างต่อไปนี้เป็นการนิยามเวกเตอร์ และเวกเตอร์ ไว้ในตัวแปร u และ v ตามลำดับ
>>> from vis import vector >>> u = vector(2,3) >>> v = vector(3,-4) >>> print u,v <2, 3, 0> <3, -4, 0>
จะเห็นว่าเวกเตอร์ที่สร้างขึ้นมีขนาด 3 มิติ อย่างไรก็ตามตัวอย่างทั้งหมดในเอกสารนี้จะสนใจเพียงสองมิติแรก ซึ่งหากไม่สนใจมิติที่สามแล้วค่าของ u และ v ข้างต้นจะสอดคล้องกับแผนภาพดังนี้
ปริมาณในแต่ละมิติของเวกเตอร์สามารถอ้างถึงผ่านคุณลักษณะชื่อ x และ y ของเวกเตอร์นั้น ๆ และยังอ้างอิงตามรูปแบบลิสต์ได้เช่นกัน ตัวอย่างเช่น
>>> v = vector(2,3) >>> print v.x,v.y 2.0 3.0 >>> print v[0],v[1] 2.0 3.0 >>> v.x = -8.5 >>> print v <-8.5, 3, 0>
การบวกและลบเวกเตอร์
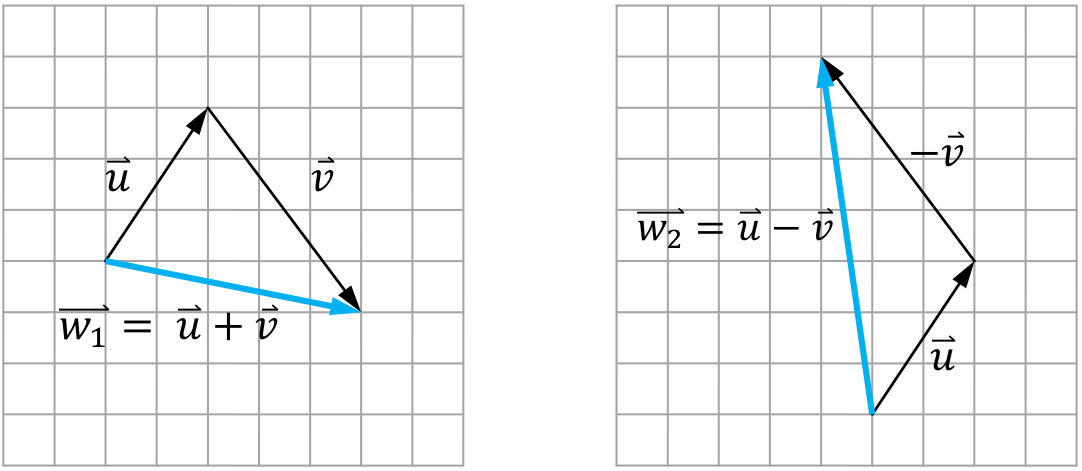
เนื่องจากภาษาไพทอนรองรับการทำ Operator Overloading ข้อมูลชนิดเวกเตอร์ที่สร้างขึ้นจากคลาส vector ของ VPython สามารถนำมาประมวลผลด้วยตัวดำเนินการทางคณิตศาสตร์ + และ – ได้ทันที ดังตัวอย่าง
>>> from vis import vector >>> u = vector(2,3) >>> v = vector(3,-4) >>> w1 = u+v >>> w2 = u-v >>> print w1,w2 <5, -1, 0> <-1, 7, 0>
ซึ่งสอดคล้องกับแผนภาพ
การคูณและหารเวกเตอร์ด้วยสเกลาร์
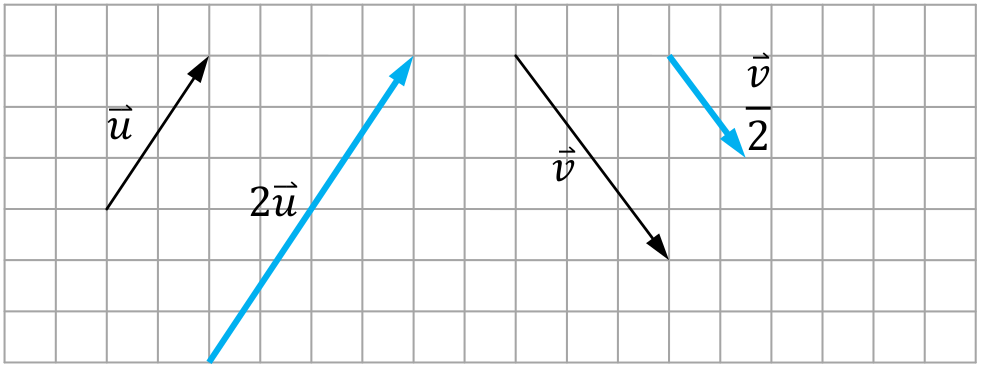
ปริมาณเวกเตอร์ที่สร้างขึ้นสามารถนำมาคูณหรือหารด้วยปริมาณสเกลาร์ผ่านตัวดำเนินการ * และ /
>>> w3 = u*2 >>> w4 = v/2 >>> print w3 <4, 6, 0> >>> print w4 <1.5, -2, 0>
ซึ่งให้ผลลัพธ์เป็นเวกเตอร์ใหม่ที่ขนาดเปลี่ยนไปแต่ยังคงทิศทางเดิม ดังแผนภาพ
ขนาดของเวกเตอร์
เวกเตอร์ 2 มิติ มีขนาด (หรือความยาว) ตามทฤษฎีของปีทาโกรัสดังนี้
ขนาดของเวกเตอร์คำนวณได้จากคุณสมบัติ mag ดังตัวอย่าง
>>> from vis import vector >>> v = vector(3,4) >>> print v.mag 5.0
ดังนั้นสำหรับเวกเตอร์ใด ๆ ที่ขนาดไม่เป็นศูนย์ เราสามารถสร้างเวกเตอร์หนึ่งหน่วยที่ชี้ไปทางเดียวกับเวกเตอร์นั้น โดยการหารเวกเตอร์นั้นด้วยขนาดของมันเอง ดังตัวอย่าง
>>> u = v/v.mag >>> print u <0.6, 0.8, 0> >>> print u.mag 1.0
การประยุกต์ใช้กฎการเคลื่อนที่เพื่อจำลองการเคลื่อนไหวของวัตถุ
กฎการเคลื่อนที่พื้นฐานกล่าวไว้ว่าสำหรับวัตถุใด ๆ แล้ว ความเร็วของวัตถุ และตำแหน่งของวัตถุ มีความสัมพันธ์ตามสมการ
ในกรณีที่ มีค่าน้อย หรือ มีค่าคงที่ ซึ่งจะได้ว่า
ซึ่งมีความหมายว่าเราสามารถทราบตำแหน่งของวัตถุหลังจากที่เวลาผ่านไป ได้โดยอาศัยความเร็วและตำแหน่งปัจจุบันของมัน
ในทำนองเดียวกัน ความสัมพันธ์ระหว่างความเร่ง และความเร็ว สามารถเขียนในรูป
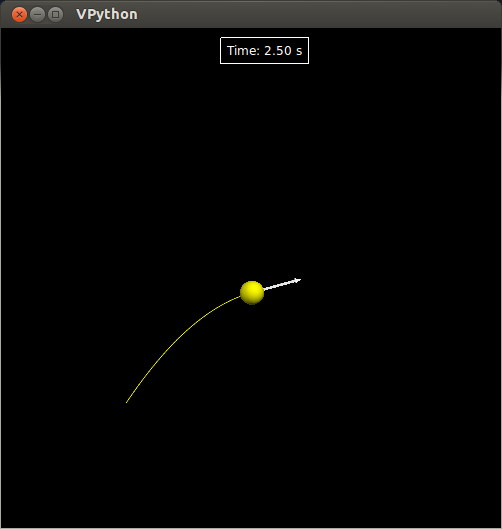
ตัวอย่างสคริปต์ด้านล่างแสดงการคำนวณความเร็วและตำแหน่งของวัตถุโดยใช้สมการการเคลื่อนที่ข้างต้นมาประมวลผลด้วยคณิตศาสตร์แบบเวกเตอร์ จากนั้นนำมาสร้างเป็นภาพเคลื่อนไหวด้วย VPython ได้ดังนี้
# set encoding=utf8
import vis
DELTA_T = 0.05
scene = vis.display(width=500,height=500)
scene.range = 100 # กำหนดช่องหน้าต่างแสดงผลให้ครอบคลุมรัศมี 100 หน่วยจากศูนย์กลางจอ
# สร้างลูกบอลสีเหลืองรัศมี 5 หน่วยไว้ที่พิกัด (-50,-50)
ball = vis.sphere(pos=(-50,-50),radius=5,color=vis.color.yellow,make_trail=True)
ball.vel = vis.vector(20,30) # กำหนดความเร็วต้นของลูกบอล
ball.acc = vis.vector(0,-9.8) # กำหนดความเร่งของลูกบอลตามแรงโน้มถ่วงของโลก
# เตรียมลูกศรเพื่อแสดงทิศทางและขนาดของความเร็วปัจจุบันของลูกบอล
arrow = vis.arrow(shaftwidth=1)
# เตรียมป้ายข้อความเพื่อใช้แสดงผลเวลาปัจจุบัน
txt = vis.label(pos=(5,90))
txt.time = 0.0
while True:
vis.rate(30) # หน่วงเวลาให้แอนิเมชันอัพเดตไม่เกิน 30 ครั้งต่อวินาที
ball.vel += ball.acc*DELTA_T # คำนวณความเร็วใหม่จากความเร่งปัจจุบัน
ball.pos += ball.vel*DELTA_T # คำนวณตำแหน่งใหม่จากความเร็วปัจจุบัน
arrow.pos = ball.pos
arrow.axis = ball.vel # ลากลูกศรแสดงทิศทางและขนาดของความเร็ว
txt.time += DELTA_T
txt.text = 'Time: %.2f s' % txt.time
ทดลองรันสคริปต์ข้างต้นควรเห็นผลลัพธ์ดังภาพ