418531 ภาคต้น 2552/โจทย์ปัญหาการค้นหาด้วยพละกำลังเยี่ยงควายถึก

ข้อ 1

[Subset Sum Problem] กำหนดเซตของจำนวนเต็ม $A=\{a_{1},a_{2},\ldots ,a_{n}\}\,$ ที่มีจำนวนสมาชิกเท่ากับ $n\,$ ตัว และกำหนดจำนวนเต็ม $S\,$ มาให้ เราต้องการตอบคำถามที่ว่่า "มีซับเซต $B\,$ บางซับเซตของ $A\,$ ที่ผลบวกของสมาชิกของมันเท่ากับ $S\,$ หรือไม่?" (กล่าวคือ เราต้องการหาเซต $B=\{b_{1},b_{2},\ldots ,b_{k}\}\subseteq A\,$ ที่ $b_{1}+b_{2}+\cdots +b_{k}=S\,$)

ยกตัวอย่างเช่น ถ้า $A=\{1,2,3,\ldots ,10\}$ และ $S=20\,$ แล้ว คำตอบของคำถามข้างบนคือ "ใ่ช่" เนื่องจากมีซับเซต $\{2,8,10\}\,$ ที่ผลบวกของมันมีค่าเท่ากับ 20 (ความจริงแล้วยังมีซับเซตอื่นๆ อีกมากมายที่มีผลบวกเท่ากับ 20) ในทางกลับกัน ถ้า $S=100\,$ แล้วเราไม่สามารถหาซับเซตของ $A\,$ ที่มีผลบวกเท่ากับ $100\,$ ได้เลย (ทำไม?)

จงออกแบบอัลกอริทึมเพื่อแก้ปัญหาข้างต้น อัลกอริทึมของคุณควรใช้เวลาทำงานไม่เกิน $O(n2^{n})\,$

เฉลย

ข้อ 2

[จิตรทัศน์ ฝักเจริญผล] แดงเตรียมตัวไปตั้งแค้มป์ในป่าดงดิบกับเพื่อนๆ เขาไปเดินเลือกซื้ออุปกรณ์ที่ห้างสรรพสินค้าโชว์ห่วย ในร้านมีอุปกรณ์ตั้งแค้มป์ $n\,$ ชิ้น ผลิตภัณฑ์ชิ้นที่ $i\,$ มีราคา $w_{i}\,$ บาท

แดงต้องการอุปกรณ์เหล่านี้ เพื่อใช้งานหลายอย่าง เช่น เหลาไม้ ขุดดิน ฟังเพลง เลื่อยไม้ กรองน้ำ ถลุงเหล็ก โม่แป้ง เป็นต้น รวมการใช้งานทั้งหมดมีได้ $k\,$ แบบ

แดงมีข้อมูลว่าอุปกรณ์แต่ละชิ้นทำอะไรได้บ้าง โดยสำหรับอุปกรณ์ที่ $i\,$ และการใช้งานที่ $j$ ค่า $p(i,j)\,$ จะระบุว่า อุปกรณ์ดังกล่าวมีความสามารถใชงานสำหรับงานที่ $j\,$ หรือไม่ กล่าวคือ $p(i,j)=1\,$ เมื่ออุปกรณ์ที่ $i\,$ สามารถทำงาน $j\,$ ได้ และ $p(i,j)=0\,$ เมื่ออุปกรณ์ชิ้นที่ i ทำไม่ได้

ช่วยแดงเลือกเซตของอุปกรณ์ที่จะซื้อเพื่อให้สามารถใช้งานทำงานทุกงานได้ครบ กล่าวคือ สำหรับการใช้งาน $j$ ใดๆ จะต้องมีอุปกรณ์ที่เลือกไปอย่างน้อย $1\,$ อย่างที่สามารถใช้ทำงาน $j\,$ ได้ นอกจากนี้ให้เลือกโดยใช้เงินน้อยที่สุดด้วย

จงออกแบบอัลกอริทึมเพื่อช่วยแดงแก้ปัญหาข้างต้น อัลกอริทึมของคุณควรใช้เวลาทำงานไม่เกิน $O(nk2^{n})\,$

หมายเหตุ: มีอัลกอริทึมที่สามารถแก้ปัญหานี้ได้ในเวลา $O(nk2^{k})\,$

เฉลย

ข้อ 3

[YTOPC Challenge เมษายน 2552] กำหนดเซตของจำนวนเต็ม $A\,$ ซึ่งมีสมาชิกอยู่ทั้งหมด $n\,$ ตัว เราต้องการตอบคำถามว่า "มีจำนวนเต็ม $a,b,c\in A$ โดยที่ $a<b<c\,$ และ $a+b>c\,$ หรือไม่?" (กล่าวอีกอย่างหนึ่งคือ $a,b,c\,$ สามารถเป็นความยาวด้านของสามเหลี่ยมรูปหนึ่งได้)

1. จงออกแบบอัลกอริทึมที่ตอบคำถามดังกล่าวข้างต้นที่มีเวลาการทำงานเท่ากับ $\Theta (n^{3})\,$
2. จงแสดงว่าถ้าเราสามารถเรียงจำนวนที่อยู่ในเซต $A\,$ ในเวลา $O(f(n))\,$ แล้วเราสามารถแก้ปัญหานี้ในเวลา $O(f(n)+n)\,$

เฉลย

ข้อ 4

[ทักษพร กิตติอัครเสถียร, TOI.C:05-2009] กำหนดเซตของจำนวนเต็ม $A\,$ ซึ่งมีสมาชิกอยู่ทั้งหมด $n\,$ ตัว และกำหนดจำนวนเต็ม $x\,$ ให้ เราต้องการตอบคำถามว่า "มีคู่จำนวนเต็ม $a,b\,$ โดยที่ $a,b\in A\,$ และ $a<b\,$ และ $a+b=x\,$ อยู่กี่คู่"

ยกตัวอย่างเช่น ถ้า $A={1,2,3,...,10}\,$ และ $x=11\,$ แล้วคำตอบของคำถามข้างต้นคือ 5 แต่ถ้า $x=19\,$ แล้วคำตอบคือ 1

1. จงออกแบบอัลกอริทึมที่ตอบคำถามดังกล่าวข้างต้นที่มีเวลาการทำงานเท่ากับ $\Theta (n^{2})\,$
2. จงแสดงว่าถ้าสามารถตอบคำถามว่ามีจำนวนเต็ม $y\,$ อยู่ในเซต $A\,$ หรือไม่ ได้ในเวลา $O(f(n))\,$ แล้วเราสามารถแก้ปัญหานี้ในเวลา $O(n\cdot f(n))\,$

เฉลย

ข้อ 5

[ข้อสอบคอมพิวเตอร์โอลิมปิกประเทศไทย ประจำปี 2548] ลำดับเลขคณิต (arithmetic sequence) คือลำดับที่ผลต่างของพจน์ที่อยู่ติดกันมีค่าคงที่ เช่น 2, 4, 6, 8, 10, 12 เป็นลำดับเลขคณิตที่มีผลต่างระหว่างพจน์ที่ติดกันเท่ากับ 2 และ 11, 6, 1, -4, -9, -14, -19 เป็นลำดับเลขคณิตที่มีผลต่างระหว่างพจน์ที่ติดกันเท่ากับ -5

กำหนดลำดับ (ที่ไม่จำเป็นต้องเป็นลำดับเลขคณิต) ของจำนวนเต็มลำดับหนึ่งมาให้ โดยลำดับนี้มีความยาว $n\,$ จงหาลำดับย่อย (หมายถึงพจน์ที่ติดกัน) ของลำดับนี้ที่มีความยาวมากทีุ่สุดและเป็นลำดับเลขคณิต

ยกตัวอย่างเช่น สมมติว่าลำดับที่ให้มาคือลำดับ 10, 1, 2, 3, 2, 4, 6, 8, 10, 5, 0 เราได้ว่ามีลำดับย่อยของลำดับนี้ที่เป็นลำดับเลขคณิตอยู่หลายลำดับ เช่น 10, 1, 2, 3, 2, 4, 6, 8, 10, 5, 0 (ความยาว 3) หรือ 10, 1, 2, 3, 2, 4, 6, 8, 10, 5, 0 (ความยาว 3) แต่ลำดับย่อยที่เป็นลำดับเลขคณิตที่ยาวที่สุดคือ 10, 1, 2, 3, 2, 4, 6, 8, 10, 5, 0 (ความยาว 5)

1. จงออกแบบอัลกอริทึมที่แก้ปัญหาข้างต้นที่มีเวลาการทำงานเท่ากับ $\Theta (n^{3})\,$
2. จงออกแบบอัลกอริทึมที่แก้ปัญหาข้างต้นที่มีเวลาการทำงานเท่ากับ $\Theta (n)\,$

เฉลย

ข้อ 6

[APIO 2009] รัฐบาลของเมืองสิรูเสรีตัดสินใจว่าจะมีการประมูลที่ดินซึ่งอุดมไปด้วย น้ำมันในจังหวัดนาวาลูร์ ให้กับบริษัทเอกชนที่สนใจจะมาขุดบ่อน้ำมัน ที่ดินที่จะเอาไปประมูลมีรูปร่างเป็นสี่เหลี่ยมผืนผ้าที่ถูกแบ่งออกเป็นตารางขนาด $M\,$ คูณ $N$ ช่อง

ก่อนหน้านี้ หน่วยสำรวจทางธรณีวิทยาของสิรูเสรีได้ประมาณปริมาณน้ำมันสะสมในนาวาลูร์ไว้ ข้อมูลที่สำรวจได้มีรูปแบบเป็นตารางขนาด $M\,$ คูณ $N\,$ ช่อง ที่แต่ละช่องบรรจุจำนวนเต็มหนึ่งค่า ซึ่งเป็นค่าประมาณของปริมาณน้ำมันสะสมในที่ดินช่องนั้น

เพื่อป้องกันการผูกขาดการขุดเจาะน้ำมัน รัฐบาลจึงออกกฎว่าบริษัทแต่ละบริษัทสามารถขอประมูลพื้นที่ซึ่งเป็นสี่เหลี่ยมจัตุรัสขนาด $K\,$ คูณ $K\,$ ช่องได้เท่านั้น

กลุ่มบริษัทน้ำมัน AoE ซึ่งประกอบด้วยบริษัทน้ำมันสามบริษัทเข้าร่วมการประมูลครั้งนี้ด้วย โดยแต่ละบริษัทต้องการที่ดินหนึ่งพื้นผืนซึ่งไม่ซ้อนทับกับที่ดินของบริษัทอื่นในกลุ่ม นอกจากนี้พวกเขายังต้องการให้ที่ดินมีปริมาณน้ำมันสะสมมากที่สุดเท่าที่จะมากได้

ตัวอย่างเช่น สมมติว่าข้อมูลปริมาณน้ำมันสะสมเป็นดังเช่นตารางข้างล่างนี้

1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1
1 8 8 8 8 8 1 1 1
1 8 8 8 8 8 1 1 1
1 8 8 8 8 8 1 1 1
1 1 1 1 8 8 8 1 1
1 1 1 1 1 1 8 8 8
1 1 1 1 1 1 9 9 9
1 1 1 1 1 1 9 9 9

ถ้า $K=2\,$ แล้วกลุ่มบริษัท AoE สามารถเลือกประมูลพื้นที่ซึ่งมีปริมาณน้ำมันสะสมรวมสูงสุด เท่ากับ 100 ได้ แต่ถ้า $K=3\,$ แล้ว AoE สามารถเลือกประมูลพื้นที่ที่มีน้ำมันสะสมรวมสูงสุด เท่ากับ 208 ได้

AoE ได้จ้างคุณให้ออกแบบอัลกอริทึมเพื่อหาปริมาณน้ำมันสะสมรวมสูงสุดที่ AoE สามารถประมูลได้

1. จงออกแบบอัลกอริืึทึมดังกล่าว อัลกอริทึมของคุณควรทำงานด้วยเวลา $\Theta (N^{3}M^{3}K^{2})\,$
2. จงออกแบบอัลกอริืึทึมดังกล่าว อัลกอริทึมของคุณควรทำงานด้วยเวลา $\Theta (N^{3}M^{3})\,$

เฉลย

ข้อ 7

[อาภาพงศ์ จันทร์ทอง, TOI.C:05-2009] เรามีลำดับของจำนวนเต็ม $N$ จำนวน แทนด้วย $a_{1},a_{2},a_{3},\ldots ,a_{N}\,$ เราต้องการทราบจำนวนของลำดับย่อย $a_{i},a_{i+1},a_{i+2},\ldots ,a_{j}\,$ (ซึ่ง $i\leq j\,$) ที่มีพิสัยของลำดับย่อยเป็นจำนวนเต็มที่อยู่ในช่วง $[p,q]\,$ ว่ามีกี่ลำดับย่อย

นิยาม: พิสัยของลำดับจำนวนหนึ่ง ๆ คือผลต่างของค่าสูงสุดและต่ำสุดของลำดับดังกล่าว ดังนั้นพิสัยของลำดับย่อย $a_{i},a_{i+1},a_{i+2},\ldots ,a_{j}\,$ ก็คือ $\max(a_{i},a_{i+1},a_{i+2},\ldots ,a_{j})-\min(a_{i},a_{i+1},a_{i+2},\ldots ,a_{j})\,$

ตัวอย่างเช่น สมมติลำดับของจำนวนเต็ม 7 ตัวมี 1, 7, 4, 3, 9, 6, 8 พบว่าจะมีลำดับย่อยทั้งหมด 13 ลำดับย่อยที่มีค่าพิสัยอยู่ในช่วงตั้งแต่ 4 ถึง 6 ได้แก่ 1-7-4-3, 1-7-4, 1-7, 7-4-3-9-6-8, 7-4-3-9-6, 7-4-3-9, 7-4-3, 4-3-9-6-8, 4-3-9-6, 4-3-9, 3-9-6-8, 3-9-6 และ 3-9

จงออกแบบอัลกอริทึมสำหรับแก้ปัญหานี้ อัลกอริทึมของคุณควรจะทำงานในเวลา $O(n^{3})\,$

หมายเหตุ: มีอัลกอริทึมที่สามารถแก้ปัญหานี้ได้ในเวลา $O(n\log n)\,$

เฉลย

ข้อ 8

[Satisfiability Problem] กำหนดประพจน์ที่มีตัวแปร $x_{1},x_{2},\ldots ,x_{n}\,$ (ตัวแปรจะมีไม่มากกว่า $n\,$ ตัว) โดยที่แต่ละตัวมีค่า $T\,$ หรือ $F\,$ และตัวแปรเหล่านี้ถูกประกอบเข้าด้วยกันเป็นประพจน์ด้วยเครื่องหมาย $\wedge \,$, $\vee \,$, และ/หรือ $\neg \,$ ยกตัวอย่างเช่น $x_{1}\wedge (x_{2}\vee \neg x_{3})\,$ หรือ $(x_{1}\vee x_{2})\wedge (x_{3}\vee x_{4}\vee x_{5})\,$ เป็นต้น

เราต้องการตอบคำถามว่า "สำหรับประพจน์ที่ให้มา มีวิธีการกำหนดค่าตัวแปรให้ประพจน์มีค่าเป็น $T\,$ หรือไม่?"

ยกตัวอย่างเ่ช่น สำหรับประพจน์ $x_{1}\wedge x_{2}\wedge \neg x_{3}$ เราสามารถทำให้ประพจน์มีค่าเป็น $T\,$ ได้ด้วยการกำหนดให้ $x_{1}=T,x_{2}=T,x_{3}=F\,$ ได้ ฉะนั้นคำตอบของคำถามข้างต้นสำหรับประพจน์นี้คือ "ใช่" แต่สำหรับประพจน์ $x_{1}\wedge \neg x_{1}\,$ แล้ว ไม่ว่าเราจะกำหนดให้ $x_{1}\,$ มีค่าเป็นอะไร ประพจน์ก็จะมีค่าเป็น $F\,$ เสมอ ดังนั้นคำตอบของคำถามนี้สำหรับประพจน์ที่สองนี้คือ "ไม่ใช่"

จงออกแบบอัลกอริทึมสำหรับแก้ปัญหาดังกล่าว อัลกอริทึมของคุณควรทำงานในเวลา $O(2^{n}M)\,$ เมื่อ $M\,$ คือเวลาที่ใช้ในการคำนวณค่าความจริงของประพจน์ที่กำหนดให้ โดยที่คุณรู้ค่าของตัวแปรทุกตัวแล้ว

เฉลย

ข้อ 9

กำหนดตารางขนาด $n$ คูณ $n$ มาให้หนึ่งตาราง ตารางแต่ละช่องมีจำนวนเต็มบวกบรรจุดอยู่หนึ่งจำนวน

เราสามารถคำนวณคะแนนของตารางได้ดังนี้: สำหรับช่องแต่ละช่องที่ไม่ใช่ช่องที่อยู่ในแถวล่างสุดหรือช่องที่อยู่ในแถวซ้ายสุด

• ให้หาผลต่างของเลขจำนวนเต็มในช่องนั้นกับช่องที่อยู่ทางด้านซ้ายของมัน แล้วนำผลลัพธ์ที่ได้ไปยกกำลังสอง
• ให้หาผลต่างของเลขจำนวนเต็มในช่องนั้นกับช่องที่อยู่ทางด้านล่างของมัน แล้วนำผลลัพธ์ที่ได้ไปยกกำลังสอง

คะแนนของตารางคือผลบวกของเลขทั้งสองตัวข้างบนนี้ สำหรับตารางช่องที่ไม่ใช่ช่องที่อยู่ในแถวล่างสุดหรือช่องที่อยู่ในแถวซ้ายสุดทุกช่อง

ยกตัวอย่างเช่น ตาราง:

5 6 4
2 3 1
8 9 7

มีคะแนนเท่ากับ $(5-6)^{2}+(5-2)^{2}+(6-4)^{2}+(6-3)^{2}+(4-1)^{2}+(2-3)^{2}+(2-8)^{2}+(3-1)^{2}+(3-9)^{2}+(1-7)^{2}+(8-9)^{2}+(9-7)^{2}=150$

คุณต้องการทำให้คะแนนของตารางมีค่าต่ำสุดเท่าที่จะเป็นไปได้ โดยคุณสามารถ

• สลับแถวของตารางแบบใดก็ได้ แต่เวลาสลับต้องสลับทั้งแถว
• สลับคอลัมน์ของตารางแบบใดก็ได้ แต่เวลาสลับต้องสลับทั้งคอลัมน์

จงออกแบบอัลกอริทึมเพื่อหาค่าที่ต่ำที่สุดนี้ อัลกอริทึมของคุณควรทำงานในเวลา $O(n^{2}n!)\,$

หมายเหตุ: มีอัลกอริทึมที่สามารถแก้ปัญหานี้ได้ในเวลา $O(n^{2}2^{n})\,$

เฉลย

ข้อ 10

[Traveling Salesman Problem] กำหนดจุดมาให้ $n\,$ ในระนาบสองมิติ ให้จุด $n\,$ จุดเหล่านี้มีสัญลักษณ์ $(x_{1},y_{1}),(x_{2},y_{2}),\ldots ,(x_{n},y_{n})\,$

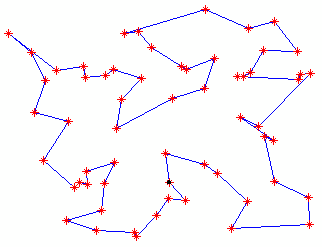
คุณต้องการเดินทางโดยเริ่มจากจุด $(x_{1},y_{1})\,$ แล้วไปผ่านจุดอื่นทุกจุด โดยคุณจะเดินเข้าหาจุดแต่ละจุดเพียงครั้งเดียว และออกจากจุดแต่ละจุดเพียงครั้งเดียวเท่านั้น แล้วให้ท้ายที่สุดคุณกลับไปอยู่ที่จุด $(x_{1},y_{1})\,$ อีกครั้ง การเดินแบบนี้เรียกว่า Hamiltonian Cycle ยกตัวอย่างเช่นตามรูปข้างล่างนี้ (จุด $(x_{1},y_{1})\,$ จะเป็นจุดใดก็ได้ในจุดหลายๆ จุดข้างล่างนี้)

คุณต้องการหา Hamiltonian Cycle ที่มีระยะทางสั้นที่สุด โดยระยะทางของ Hamiltonian Cycle หนึ่งๆ มีค่าเท่ากับผลบวกของความยาวของส่วนของเส้นตรงที่เชื่อมจุดสองจุดที่คุณเดินระหว่างมันในเส้นทาง คุณคงยังจำได้ว่าระยะทางระหว่างจุด $(x_{i},y_{i})\,$ และ $(x_{j},y_{j})\,$ มีค่าเท่ากับ ${\sqrt {(x_{i}-x_{j})^{2}+(y_{i}-y_{j})^{2}}}\,$ ดังนั้นถ้าสมมติให้ $n=4\,$ เราจะได้ว่า Hamiltonian Cycle $(x_{1},y_{1})\rightarrow (x_{4},y_{4})\rightarrow (x_{2},y_{2})\rightarrow (x_{3},y_{3})\rightarrow (x_{1},y_{1})\,$ มีระยะทางเท่ากับ ${\sqrt {(x_{1}-x_{4})^{2}+(y_{1}-y_{4})^{2}}}+{\sqrt {(x_{4}-x_{2})^{2}+(y_{4}-y_{2})^{2}}}+{\sqrt {(x_{2}-x_{3})^{2}+(y_{2}-y_{3})^{2}}}+{\sqrt {(x_{3}-x_{1})^{2}+(y_{3}-y_{1})^{2}}}\,$

จงออกแบบอัลกอริืทึมเพื่อแก้ปัญหานี้ อัลกอริทึมของคุณควรทำงานได้ในเวลา $O(n!)\,$

เฉลย