ผลต่างระหว่างรุ่นของ "418531 ภาคต้น 2552/โจทย์ปัญหาอัลกอริทึมแบบตะกละ II/เฉลยข้อ 4"
Cardcaptor (คุย | มีส่วนร่วม) (หน้าที่ถูกสร้างด้วย '== ข้อย่อย 1 == ไม่จริง พิจารณากราฟข้างล่างและต้นไม้…') |
Cardcaptor (คุย | มีส่วนร่วม) |
||
| แถว 4: | แถว 4: | ||
[[Image:Minimum-bottleneck-spanning-tree-counterexample.JPG]] | [[Image:Minimum-bottleneck-spanning-tree-counterexample.JPG]] | ||
| − | เราได้ว่า <math>T \,</math> เป็น minimum bottleneck spanning tree ของ <math>G \,</math> เนื่องจาก spanning tree ทุกต้นต้องมี edge ที่มี cost เท่ากับ 3 แต่ <math>T \,</math> ไม่ใช่ minimum spanning tree เนื่องจากมันไม่มี edge ที่มี weight 1 | + | เราได้ว่า <math>T \,</math> เป็น minimum-bottleneck spanning tree ของ <math>G \,</math> เนื่องจาก spanning tree ทุกต้นต้องมี edge ที่มี cost เท่ากับ 3 แต่ <math>T \,</math> ไม่ใช่ minimum spanning tree เนื่องจากมันไม่มี edge ที่มี weight 1 |
| + | |||
| + | == ข้อย่อย 2 == | ||
| + | จริง | ||
| + | |||
| + | ให้ <math>T \,</math> เป็น minimum spannning tree สมมติเพื่อให้เกิดข้อขัดแย้งว่ามันไม่ใช่ minimum-bottleneck spanning tree กล่าวคือมันมี edge <math>e \,</math> ที่มี cost มากกว่า bottleneck edge ของ minimum-bottleneck spanning tree | ||
| + | |||
| + | สมมติให้ <math>T' \,</math> เป็น minimum-bottleneck spanning tree ต้นหนึ่ง เราได้ว่า cost ของ edge ทุก edge ใน <math>T' \,</math> จะมีค่าน้อยกว่า cost ของ edge <math>e \,</math> ดังนั้น เมื่อเราเพิ่ม <math>e \,</math> เข้าไปใน <math>T' \,</math> มันจะทำให้เกิด cycle ขึ้นหนึ่ง cycle และเรายังทราบอีกว่า <math>e \,</math> จะเป็น edge ที่มี cost มากที่สุดใน cycle นั้น จาก cycle property เราทราบว่า <math>e \,</math> จะต้องไม่เป็นสมาชิกของ minimum spanning tree ต้นใดเลย เกิดข้อขัดแย้ง | ||
รุ่นแก้ไขปัจจุบันเมื่อ 15:42, 18 กันยายน 2552
ข้อย่อย 1
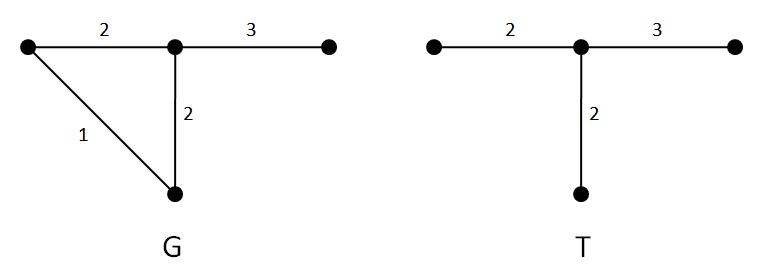
ไม่จริง พิจารณากราฟข้างล่างและต้นไม้ต้นต่อไปนี้
เราได้ว่า เป็น minimum-bottleneck spanning tree ของ เนื่องจาก spanning tree ทุกต้นต้องมี edge ที่มี cost เท่ากับ 3 แต่ ไม่ใช่ minimum spanning tree เนื่องจากมันไม่มี edge ที่มี weight 1
ข้อย่อย 2
จริง
ให้ เป็น minimum spannning tree สมมติเพื่อให้เกิดข้อขัดแย้งว่ามันไม่ใช่ minimum-bottleneck spanning tree กล่าวคือมันมี edge ที่มี cost มากกว่า bottleneck edge ของ minimum-bottleneck spanning tree
สมมติให้ เป็น minimum-bottleneck spanning tree ต้นหนึ่ง เราได้ว่า cost ของ edge ทุก edge ใน จะมีค่าน้อยกว่า cost ของ edge ดังนั้น เมื่อเราเพิ่ม เข้าไปใน มันจะทำให้เกิด cycle ขึ้นหนึ่ง cycle และเรายังทราบอีกว่า จะเป็น edge ที่มี cost มากที่สุดใน cycle นั้น จาก cycle property เราทราบว่า จะต้องไม่เป็นสมาชิกของ minimum spanning tree ต้นใดเลย เกิดข้อขัดแย้ง