ผลต่างระหว่างรุ่นของ "418531 ภาคต้น 2552/โจทย์ปัญหาอัลกอริทึมแบบตะกละ II/เฉลยข้อ 2"

รุ่นแก้ไขปัจจุบันเมื่อ 10:12, 6 ตุลาคม 2552

ข้อย่อย 1

เราจะทำการพิสูจน์โดยใช้ข้อสังเกตต่อไปนี้

สำหรับ edge $e\,$ และ edge $e'\,$ ในกราฟ ถ้า $c(e)<c(e')\,$ แล้ว $c(e)^{2}<c(e')^{2}\,$ ด้วย

พิสูจน์:

จาก

c(e)<c(e')\,

ให้เป็นสมการที่ 1

คูณสมการที่ 1 ทั้งสองข้างด้วย

c(e)\,

จะได้

c(e)^{2}<c(e')c(e)\,

ให้เป็นสมการที่ 2 (เนื่องจาก cost ของทุก edge เป็นบวก)

คูณสมการที่ 1 ทั้งสองข้างด้วย

c(e')\,

จะได้

c(e)c(e')<c(e')^{2}\,

ให้เป็นสมการที่ 3 (เนื่องจาก cost ของทุก edge เป็นบวก)

จากสมการที่ 2 และ 3 จะได้

c(e)^{2}<c(e')^{2}\,

จริง

จะพิสูจน์ว่า minimum spanning tree $T\,$ จากกราฟ $G\,$ ที่ได้เป็น minimum spanning tree ของกราฟใหม่จริง

ดังนั้นต้องทำการพิสูจน์ว่าสำหรับทุก ๆ edge $e={a,b}\,$ ใน minimum spanning tree $T\,$ นั้น edge $e\,$ ดังกล่าวจะต้องเป็นเป็น edge ใน minmimum spanning tree ต้นหนึ่งของกราฟ $G'\,$ ด้วย

พิจารณา edge $e=\{a,b\}\,$ ใด ๆ ที่อยู่ในต้นไม้ $T\,$ ถ้าเราทำการลบ edge $e\,$ นี้ออกจากต้นไม้ $T\,$ เราจะได้ว่าเกิดการแบ่ง vertex ของกราฟ $G\,$ ออกเป็นสองส่วน ให้เป็น $A\,$ กับ $B\,$ โดยที่ $A\,$ คือเซตของ vertex ที่ไปถึงจาก $a\,$ ได้ ในกราฟ $T\,$ ที่ลบ edge $e\,$ ออกแล้ว ส่วน $B\,$ คือเซตของ vertex ที่ไปถึงจาก $b\,$ ได้ ในกราฟ $T\,$ ที่ลบ edge $e\,$ ออกแล้ว สังเกตว่า $A\,$ และ $B\,$ ไม่เป็นเซตว่าง เนื่องจาก ทั้งสองเซตจะมีสมาชิกอยู่อย่างน้อยหนึ่งตัวคือ $a\,$ และ $b\,$ ตามลำดับ นอกจากนี้ยังได้ว่า $A\cup B=V\,$ ดังนั้น $A\,$ เป็น cut ใน $G\,$

พิจารณา cut set ของ cut $A\,$ เราจะได้ว่า edge $e\,$ เป็น edge ที่มี cost น้อยที่สุดในบรรดา edge ที่ข้าม cut $A\,$ เนื่องจาก edge $e\,$ มีปลายด้านหนึ่งอยู่ใน $A\,$ และปลายอีกด้านหนึ่งอยู่ใน $B\,$ (ถ้าไม่เช่นนั้น เราสามารถเลือก edge ที่มี cost น้อยกว่า edge $e\,$ นี้มาใส่ใน tree แทน เราก็จะได้ tree อีกต้นที่มี cost น้อยกว่า cost ของ $T\,$ จึงขัดแย้งกับที่บอกว่า $T\,$ เป็น minimum spanning tree ใน $G\,$ )

พิจารณา cut $A\,$ ซึ่งเป็น cut เดียวกับที่นิยามข้างต้นในกราฟ $G'\,$ จากที่เราได้ทำการพิสูจน์ไปแล้ว จะได้ว่า cost ของ edge $e\,$ ในกราฟ $G'\,$ ซึ่งมีค่าเป็น $c(e)^{2}\,$ นี้จะต้องน้อยที่สุดในบรรดา edge ที่ข้าม cut $A\,$ ในกราฟ $G'\,$ ด้วย นั่นคือ $c(e)<c(e')\,$ สำหรับ edge $e'\,$ ใด ๆ ที่เป็น edge ข้าม cut $A\,$ และ $e\neq e'\,$ แล้ว $c(e)^{2}<c(e')^{2}\,$ และเนื่องจากโจทย์กำหนดให้ cost ของแต่ละ edge ในกราฟไม่ซ้ำกัน จาก cut property เราจะได้ว่า edge $e\,$ นี้จะต้องเป็น edge ใน minimum spanning tree ต้นหนึ่งของกราฟ $G'\,$

ข้อย่อย 2

ข้อความข้างต้นไม่จริง แสดงตัวอย่างขัดแย้งได้ดังต่อไปนี้

จากตัวอย่างข้างต้น กราฟทางซ้ายเป็นกราฟที่ให้มา จากกราฟจะได้ระยะทางที่สั้นที่สุดจาก $s\,$ ไป $t\,$ คือ edge ที่พุ่งจาก $s\,$ ไปยัง $t\,$ เลย ซึ่งมี cost เป็น 10 แต่เมื่อเอาค่า cost ของแต่ละ edge มายกกำลังสองแล้วจะได้ว่า ระยะทางจาก $s\,$ ไป $t\,$ จะเป็น $s\rightarrow a\rightarrow b\rightarrow t\,$ ซึ่งมี cost เป็น 4+16+49 = 69 ซึ่งน้อยกว่า cost ของedge จาก $s\,$ ไปยัง $t\,$ ที่เคยเป็นระยะทางที่สั้นที่สุดจากกราฟตั้งต้น ซึ่งตอนนี้มี cost เป็น 100

@@ แถว 9: / แถว 9: @@
 :คูณสมการที่ 1 ทั้งสองข้างด้วย <math> c(e') \,</math> จะได้ <math> c(e)c(e') < c(e')^2 \,</math> ให้เป็นสมการที่ 3 (เนื่องจาก cost ของทุก edge เป็นบวก)
 :จากสมการที่ 2 และ 3 จะได้ <math> c(e)^2 < c(e')^2 \,</math> จริง
 จะพิสูจน์ว่า minimum spanning tree <math> T \, </math> จากกราฟ <math> G \,</math> ที่ได้เป็น minimum spanning tree ของกราฟใหม่จริง
-''พิสูจน์:'' จะพิสูจน์โดยข้อขัดแย้ง สมมติให้ <math> T \, </math>  ไม่เป็น minimum spanning tree ของกราฟใหม่ ให้ minimum spanning tree ของกราฟใหม่เป็น <math> T' \,</math> แสดงว่า tree <math> T' \,</math> ต้องมี edge อย่างน้อยหนึ่ง edge ที่ไม่อยู่ใน <math> T \,</math> ให้ edge นั้นเป็น edge <math> e = \{ u,v \} \,</math> เมื่อเราลบ edge <math> e \,</math> นี้ออกจาก <math> T' \, </math> จะได้แบ่ง vertex ของกราฟออกเป็นสองส่วน ให้เป็นเซต <math> S \,</math> กับ <math> V - S \,</math> เนื่องจาก edge <math> e \, </math> เป็น edge ที่มีจุดปลายข้างหนึ่งในเซต <math> S \, </math> และปลายอีกข้างหนึ่งอยู่ใน <math> V - S \,</math> (เป็น edge ข้าม cut นั่นเอง) และ edge <math> e \, </math> นี้อยู่ใน minimum spanning tree <math> T' \,</math> ดังนั้น edge <math> e \, </math> ต้องมี cost น้อยที่สุดในบรรดา edge ข้าม cut <math> S \, </math> และ <math> V - S \, </math> นี้แล้ว หรือพูดอีกอย่างคือ <math> c(e) < c(e') \,</math> สำหรับ edge <math> e' \,</math> ใด ๆ ที่เป็น edge ข้าม cut และ <math> e \neq e' \,</math> ซึ่งจากข้อสังเกตข้างต้น เราจะได้ว่า <math> c(e)^2 < c(e')^2 \,</math> ด้วย และเนื่องจากโจทย์กำหนดให้ cost ของแต่ละ edge ในกราฟไม่ซ้ำกัน ดังนั้นในกราฟใหม่ edge <math> e \,</math> นี้ก็จะต้องถูกเพิ่มเข้าไปใน minimum spanning tree ด้วย เนื่องจากเป็น edge ข้าม cut ที่มี cost น้อยที่สุดแล้ว  จึงเกิดข้อขัดแย้ง ดังนั้น mimimum spanning tree <math> T \,</math> ที่ได้จากกราฟ <math> G \,</math> จะเป็น minimum spanning tree ของกราฟใหม่ด้วย
+ดังนั้นต้องทำการพิสูจน์ว่าสำหรับทุก ๆ edge <math> e={a,b}\,</math> ใน minimum spanning tree <math> T\,</math> นั้น edge <math> e \,</math> ดังกล่าวจะต้องเป็นเป็น edge ใน minmimum spanning tree ต้นหนึ่งของกราฟ <math> G' \, </math> ด้วย
+พิจารณา edge <math> e=\{a,b\} \,</math> ใด ๆ ที่อยู่ในต้นไม้ <math> T \,</math> ถ้าเราทำการลบ edge <math> e \,</math> นี้ออกจากต้นไม้ <math> T \,</math> เราจะได้ว่าเกิดการแบ่ง vertex ของกราฟ <math> G \,</math> ออกเป็นสองส่วน ให้เป็น <math> A \,</math> กับ <math> B\,</math> โดยที่ <math> A\,</math> คือเซตของ vertex ที่ไปถึงจาก <math> a \,</math> ได้ ในกราฟ <math> T\,</math> ที่ลบ edge <math> e\,</math> ออกแล้ว ส่วน <math> B \,</math> คือเซตของ vertex ที่ไปถึงจาก <math> b \,</math> ได้ ในกราฟ <math> T\,</math> ที่ลบ edge <math> e\,</math> ออกแล้ว สังเกตว่า <math> A \,</math> และ <math> B \,</math> ไม่เป็นเซตว่าง เนื่องจาก ทั้งสองเซตจะมีสมาชิกอยู่อย่างน้อยหนึ่งตัวคือ <math> a \,</math> และ <math> b\,</math> ตามลำดับ นอกจากนี้ยังได้ว่า <math> A \cup B = V \,</math> ดังนั้น <math> A \,</math> เป็น cut ใน <math> G \,</math>
+พิจารณา cut set ของ cut <math> A \,</math> เราจะได้ว่า edge <math> e \,</math> เป็น edge ที่มี cost น้อยที่สุดในบรรดา edge ที่ข้าม cut <math> A \,</math> เนื่องจาก edge <math> e \,</math> มีปลายด้านหนึ่งอยู่ใน <math> A \,</math> และปลายอีกด้านหนึ่งอยู่ใน <math> B \,</math> (ถ้าไม่เช่นนั้น เราสามารถเลือก edge ที่มี cost น้อยกว่า edge <math> e \,</math> นี้มาใส่ใน tree แทน เราก็จะได้ tree อีกต้นที่มี cost น้อยกว่า cost ของ <math> T \,</math> จึงขัดแย้งกับที่บอกว่า <math> T \,</math> เป็น minimum spanning tree ใน <math> G \,</math>)
+พิจารณา cut <math> A \,</math> ซึ่งเป็น cut เดียวกับที่นิยามข้างต้นในกราฟ <math> G' \,</math> จากที่เราได้ทำการพิสูจน์ไปแล้ว จะได้ว่า cost ของ edge <math> e \,</math> ในกราฟ <math> G' \,</math> ซึ่งมีค่าเป็น <math> c(e)^2 \,</math> นี้จะต้องน้อยที่สุดในบรรดา edge ที่ข้าม cut <math> A \,</math> ในกราฟ <math> G' \,</math> ด้วย นั่นคือ<math> c(e) < c(e') \,</math> สำหรับ edge <math> e' \,</math> ใด ๆ ที่เป็น edge ข้าม cut <math> A \,</math> และ <math> e \neq e' \,</math> แล้ว <math> c(e)^2 < c(e')^2 \,</math> และเนื่องจากโจทย์กำหนดให้ cost ของแต่ละ edge ในกราฟไม่ซ้ำกัน  จาก cut property เราจะได้ว่า edge <math> e \,</math> นี้จะต้องเป็น edge ใน minimum spanning tree ต้นหนึ่งของกราฟ <math> G'\,</math>
 ==ข้อย่อย 2 ==
 ข้อความข้างต้นไม่จริง แสดงตัวอย่างขัดแย้งได้ดังต่อไปนี้
+[[ไฟล์:2_2.JPG]]
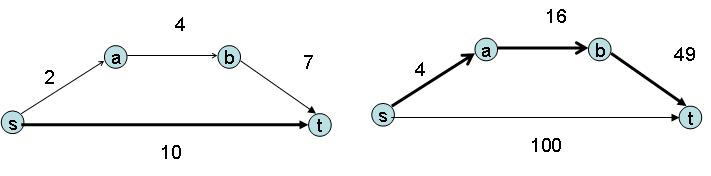
+จากตัวอย่างข้างต้น กราฟทางซ้ายเป็นกราฟที่ให้มา จากกราฟจะได้ระยะทางที่สั้นที่สุดจาก <math> s \, </math> ไป <math> t \,</math> คือ edge ที่พุ่งจาก <math> s \, </math> ไปยัง <math> t \, </math> เลย ซึ่งมี cost เป็น 10 แต่เมื่อเอาค่า cost ของแต่ละ edge มายกกำลังสองแล้วจะได้ว่า ระยะทางจาก <math> s \,</math> ไป <math> t \,</math> จะเป็น <math> s \rightarrow a \rightarrow b \rightarrow t \,</math> ซึ่งมี cost เป็น 4+16+49 = 69 ซึ่งน้อยกว่า cost ของedge จาก <math> s \, </math> ไปยัง <math> t \,</math> ที่เคยเป็นระยะทางที่สั้นที่สุดจากกราฟตั้งต้น ซึ่งตอนนี้มี cost เป็น 100

ผลต่างระหว่างรุ่นของ "418531 ภาคต้น 2552/โจทย์ปัญหาอัลกอริทึมแบบตะกละ II/เฉลยข้อ 2"

รุ่นแก้ไขปัจจุบันเมื่อ 10:12, 6 ตุลาคม 2552

ข้อย่อย 1

ข้อย่อย 2

รายการเลือกการนำทาง

เครื่องมือส่วนตัว

เนมสเปซ

สิ่งที่แตกต่าง

ดู

เพิ่มเติม

ค้นหา

การนำทาง

เครื่องมือ