ผลต่างระหว่างรุ่นของ "204512-53/lecture2"
Wanchat111 (คุย | มีส่วนร่วม) |
|||
| (ไม่แสดง 62 รุ่นระหว่างกลางโดยผู้ใช้ 5 คน) | |||
| แถว 1: | แถว 1: | ||
| + | =Loop Invariants= | ||
| + | |||
| + | * การเรียงข้อมูล ยกตัวอย่าง | ||
| + | #Insertion Sort | ||
| + | #Bubble Sort | ||
| + | |||
| + | =Insertion Sort= | ||
| + | |||
| + | ===Algorithm=== | ||
| + | 1. for i = 2 to n (พิจารณาข้อมูล array A[i]) | ||
| + | |||
| + | 2. x <math>\Leftarrow</math> A[i] , j <math>\Leftarrow</math> (i - 1) | ||
| + | |||
| + | 3. While (i > 0) and (A[j] > x) | ||
| + | |||
| + | A[j+1] <math>\Leftarrow</math> A[j] | ||
| + | |||
| + | j <math>\Leftarrow</math> j-1 | ||
| + | |||
| + | A[j+1] = x | ||
| + | |||
| + | ===Loop Invariants=== | ||
| + | 1. I จริงก่อนทำ (Initialization) | ||
| + | 2. ทุกๆรอบหลัง loop ทำเสร็จ I ก็จริง (Maintainance) | ||
| + | 3. ถ้า loop จบการทำงาน +I (Termination) | ||
| + | เป้าหมายก็คือโปรแกรมถูกต้องตรงกับ termination ที่เราต้องการ | ||
| + | |||
| + | ===Proof=== | ||
| + | 1. I : A[1,...,i-1] เป็นข้อมูลชุดเดียวกับ A[1,....,i-1]ตั้งต้นและเรียงลำดับจากน้อยไปมาก | ||
| + | |||
| + | 2. รอบที่ K ใดๆ i = k A[1,...,k-1] A[k] | ||
| + | . ตัวที่ 1 ... k-1 K | ||
| + | . | ||
| + | . | ||
| + | . | ||
| + | i = k+1 A[1,....,k](เรียงตามลำดับ) | ||
| + | |||
| + | ถ้า loop Invariants จริง โปรแกรมทำงานเรื่อย จะหยุดทำงานเมื่อเงื่อนไขไม่จริง | ||
| + | |||
| + | =Bubble Sort= | ||
| + | |||
| + | พิจารณา array A = [2,1,3,4,6,5,7,9,10] | ||
| + | |||
| + | ===Algorithm=== | ||
| + | 1. for j <math>\Leftarrow</math> 1 to n | ||
| + | 2. i <math>\Leftarrow</math> 1 | ||
| + | 3. while i<n | ||
| + | 4. if A[i]>A[i+1] | ||
| + | 5. swap(A[i],A[i+1]) | ||
| + | 6. i <math>\Leftarrow</math> i+1 | ||
| + | |||
| + | ===Loop Invariant=== | ||
| + | |||
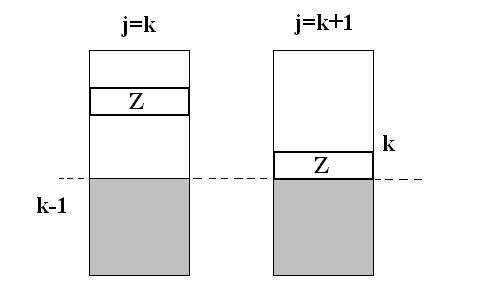
| + | I1: "A ช่อง j-1 ช่องสุดท้ายเรียงลำดับจากน้อยไปมาก และเป็นข้อมูล j-1 ตัวที่มีค่ามากที่สุดใน A" | ||
| + | |||
| + | [[ไฟล์:I1.jpg]] | ||
| + | |||
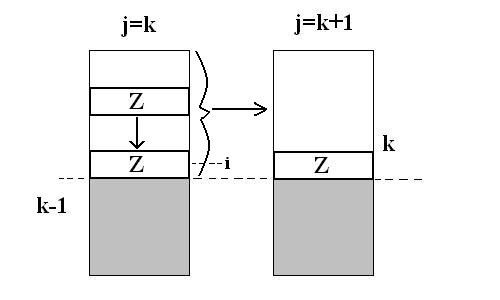
| + | I2: "A[i] มีค่ามากสุดในบรรดา A[1,...,i]" | ||
| + | |||
| + | ====Proof I2==== | ||
| + | |||
| + | 1. เริ่มต้น i=1 เห็นตัวเดียว เพราะฉะนั้น Initial จริง | ||
| + | |||
| + | 2. ตาม if ถ้าตัวที่ i มากกว่า i+1 ก็สลับ เพราะฉะนั้น i เป็นตัวที่มากสุึด | ||
| + | |||
| + | [[ไฟล์:I2.jpg]] | ||
| + | |||
| + | 3.โปรแกรมทำงานเรื่อย จะหยุดทำงานเมื่อเงื่อนไขไม่จริง | ||
| + | |||
| + | =BIG O= | ||
| + | ==Definition== | ||
| + | function f(n) เป็น O(g(n)) หรือ f(n) = O(g(n)) | ||
| + | |||
| + | ถ้ามี n<sub>0</sub> และ c(คือค่าคงที่) ที่ | ||
| + | |||
| + | f(n) ≤ c.g(n) โดยที่ n ≥ n<sub>0</sub> | ||
| + | |||
| + | ===ตัวอย่าง กราฟ Big O=== | ||
| + | |||
| + | [[ไฟล์:BigO.jpg]] | ||
| + | |||
| + | ==ตัวอย่าง1== | ||
| + | |||
| + | พิสูจน์ 1000n = O(n<sup>2</sup>) | ||
| + | |||
| + | ถ้า n > 1000 <math>\Rightarrow</math> n<sup>2</sup> ≥ 1000n | ||
| + | |||
| + | ให้ n<sub>0</sub> = 1001 , c = 1 <math>\Rightarrow</math> 1000n ≤ 1n<sup>2</sup> | ||
| + | |||
| + | เมื่อ n ≥ 1001 | ||
| + | |||
| + | =Binary Search Tree= | ||
| + | |||
| + | ===ตัวอย่าง Binary Tree=== | ||
| + | |||
| + | [[ไฟล์:BST.JPG]] | ||
| + | |||
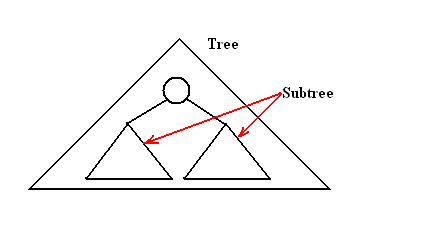
| + | ===ตัวอย่าง Subtree=== | ||
| + | |||
| + | [[ไฟล์:Tree_subtree.PNG]] | ||
| + | |||
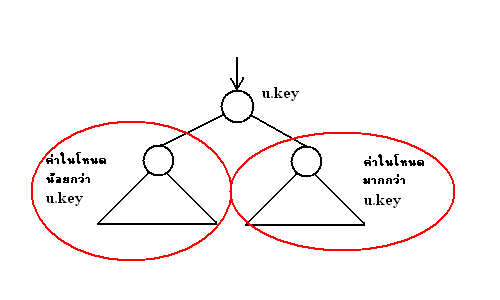
| + | ===ตัวอย่างการเก็บค่าใน Tree=== | ||
| + | |||
| + | [[ไฟล์:Tree_value.PNG]] | ||
| + | |||
| + | ===Function=== | ||
| + | |||
| + | เมื่อ x=>root, k=>key | ||
| + | |||
| + | * INSERT(x,k) | ||
| + | * FIND(x,k) | ||
| + | * MIN(x) -ไล่ tree ทางด้านซ้าย | ||
| + | * MAX(x) -ไล่ tree ทางด้านขวา | ||
| + | * SUCCESSOR(x,k) -หาตัวถัดไปที่ติดกับมันหลังเรียง | ||
| + | * DELETE(x,k) | ||
| + | |||
| + | ===FIND(x,k)=== | ||
| + | |||
| + | if x=NIL return NIL | ||
| + | if x.key=k | ||
| + | return x | ||
| + | else if x.key<k | ||
| + | return FIND(x.right,k) | ||
| + | else | ||
| + | return FIND(x.left,k) | ||
| + | |||
| + | ===อื่นๆ=== | ||
| + | |||
| + | * ความลึกของ Tree - ความยาวสูงสุดจาก root ถึง leaf (ที่ root ลึก 0) | ||
| + | |||
| + | * มีข้อมูล n ตัว สูงอย่างน้อย log n | ||
| + | |||
=Red-Black Trees= | =Red-Black Trees= | ||
| − | + | * เป็น Binary tree | |
| − | + | * Assume ว่าทุก node จบลงที่ Nil Node(All leaf node is Nil) | |
==เงื่อนไข== | ==เงื่อนไข== | ||
| − | + | * Node ใดๆจะเป็นสีแดงไม่ก็ดำ | |
| − | + | * Root เป็นสีดำ | |
| − | + | * Leaf เป็นสีดำ | |
| − | + | * Node ใดเป็น Red Node Child ของ Node นั้นจะต้องเป็น Black Node | |
| − | + | * จาก Node u ใดๆทุกๆ Path จาก Node ดังกล่าวไปยัง Leaf ของมันจะต้องมี Node ที่เป็นสีดำเท่ากันทั้งหมด | |
==Lemma== | ==Lemma== | ||
Red-Black tree ที่มี n internal nodes จะมีความสูงไม่เกิน 2log(n+1) | Red-Black tree ที่มี n internal nodes จะมีความสูงไม่เกิน 2log(n+1) | ||
| − | ==Proof== | + | ===Proof=== |
นิยาม ที่ Node u ใดๆ bh(u) (black height ของ u) จะเท่ากับจำนวน Black Node จาก u ไป Node Leaf ใดๆ(ไม่นับ u)) | นิยาม ที่ Node u ใดๆ bh(u) (black height ของ u) จะเท่ากับจำนวน Black Node จาก u ไป Node Leaf ใดๆ(ไม่นับ u)) | ||
| − | Claim สำหรับ internal node u ใดๆจำนวน internal node ใน sub-tree ใดๆที่ u เป็น rootจะมีค่าไม่น้อยกว่า 2^bh(u) -1 | + | ===Claim=== |
| + | สำหรับ internal node u ใดๆจำนวน internal node ใน sub-tree ใดๆที่ u เป็น rootจะมีค่าไม่น้อยกว่า 2^bh(u) -1 | ||
| − | Proof (By induction) | + | ===Proof (By induction)=== |
ให้ w = u.left และ h = u.right | ให้ w = u.left และ h = u.right | ||
| − | bh(w) ≥ bh(u) – 1 | + | |
| − | bh(x) ≥ bh(u) – 1 | + | bh(w) ≥ bh(u) – 1 |
| − | โดย Induction | + | |
| − | + | bh(x) ≥ bh(u) – 1 | |
| − | + | ||
| + | โดย Induction | ||
| + | |||
| + | Sub-tree ของ w มี internal node ≥ 2^bh(w) -1 ≥ 2^(bh(u)-1) -1 | ||
| + | |||
| + | Sub-tree ของ x มี internal node ≥ 2^bh(x) -1 ≥ 2^(bh(u)-1) -1 | ||
| + | |||
ดังนั้น internal node ของ u = 1 + 2^(bh(u)-1) -1 + 2^(bh(u)-1) -1 = 2^bh(u) -1 | ดังนั้น internal node ของ u = 1 + 2^(bh(u)-1) -1 + 2^(bh(u)-1) -1 = 2^bh(u) -1 | ||
| + | |||
พิจารณา Red-Black Tree ใดๆสูง h | พิจารณา Red-Black Tree ใดๆสูง h | ||
| − | + | ||
| − | + | bh(h) ≥ h/2 (เนื่องจาก Red Node จะต้องตามด้วย Black Node เสมอ) | |
| − | + | ||
| − | + | จะได้ Internal node (n) | |
| − | + | ||
| − | + | n ≥ 2^bh(h) -1 | |
| − | + | ||
| + | n ≥ 2^(h/2)-1 | ||
| + | |||
| + | n+1 ≥ 2^(h/2) | ||
| + | |||
| + | log(n+1) ≤ h/2 | ||
| + | |||
| + | h ≤2log(n+1) | ||
รุ่นแก้ไขปัจจุบันเมื่อ 11:16, 8 กรกฎาคม 2553
เนื้อหา
Loop Invariants
- การเรียงข้อมูล ยกตัวอย่าง
- Insertion Sort
- Bubble Sort
Insertion Sort
Algorithm
1. for i = 2 to n (พิจารณาข้อมูล array A[i])
2. x A[i] , j (i - 1)
3. While (i > 0) and (A[j] > x)
A[j+1] A[j]
j j-1
A[j+1] = x
Loop Invariants
1. I จริงก่อนทำ (Initialization) 2. ทุกๆรอบหลัง loop ทำเสร็จ I ก็จริง (Maintainance) 3. ถ้า loop จบการทำงาน +I (Termination) เป้าหมายก็คือโปรแกรมถูกต้องตรงกับ termination ที่เราต้องการ
Proof
1. I : A[1,...,i-1] เป็นข้อมูลชุดเดียวกับ A[1,....,i-1]ตั้งต้นและเรียงลำดับจากน้อยไปมาก
2. รอบที่ K ใดๆ i = k A[1,...,k-1] A[k]
. ตัวที่ 1 ... k-1 K
.
.
.
i = k+1 A[1,....,k](เรียงตามลำดับ)
ถ้า loop Invariants จริง โปรแกรมทำงานเรื่อย จะหยุดทำงานเมื่อเงื่อนไขไม่จริง
Bubble Sort
พิจารณา array A = [2,1,3,4,6,5,7,9,10]
Algorithm
1. for j 1 to n 2. i 1 3. while i<n 4. if A[i]>A[i+1] 5. swap(A[i],A[i+1]) 6. i i+1
Loop Invariant
I1: "A ช่อง j-1 ช่องสุดท้ายเรียงลำดับจากน้อยไปมาก และเป็นข้อมูล j-1 ตัวที่มีค่ามากที่สุดใน A"
I2: "A[i] มีค่ามากสุดในบรรดา A[1,...,i]"
Proof I2
1. เริ่มต้น i=1 เห็นตัวเดียว เพราะฉะนั้น Initial จริง
2. ตาม if ถ้าตัวที่ i มากกว่า i+1 ก็สลับ เพราะฉะนั้น i เป็นตัวที่มากสุึด
3.โปรแกรมทำงานเรื่อย จะหยุดทำงานเมื่อเงื่อนไขไม่จริง
BIG O
Definition
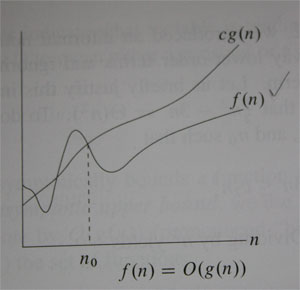
function f(n) เป็น O(g(n)) หรือ f(n) = O(g(n))
ถ้ามี n0 และ c(คือค่าคงที่) ที่
f(n) ≤ c.g(n) โดยที่ n ≥ n0
ตัวอย่าง กราฟ Big O
ตัวอย่าง1
พิสูจน์ 1000n = O(n2)
ถ้า n > 1000 n2 ≥ 1000n
ให้ n0 = 1001 , c = 1 1000n ≤ 1n2
เมื่อ n ≥ 1001
Binary Search Tree
ตัวอย่าง Binary Tree
ตัวอย่าง Subtree
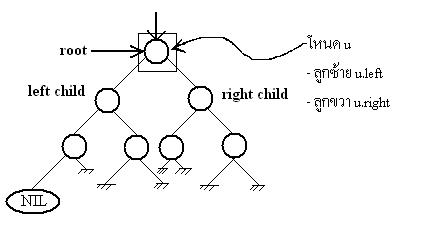
ตัวอย่างการเก็บค่าใน Tree
Function
เมื่อ x=>root, k=>key
- INSERT(x,k)
- FIND(x,k)
- MIN(x) -ไล่ tree ทางด้านซ้าย
- MAX(x) -ไล่ tree ทางด้านขวา
- SUCCESSOR(x,k) -หาตัวถัดไปที่ติดกับมันหลังเรียง
- DELETE(x,k)
FIND(x,k)
if x=NIL return NIL
if x.key=k
return x
else if x.key<k
return FIND(x.right,k)
else
return FIND(x.left,k)
อื่นๆ
- ความลึกของ Tree - ความยาวสูงสุดจาก root ถึง leaf (ที่ root ลึก 0)
- มีข้อมูล n ตัว สูงอย่างน้อย log n
Red-Black Trees
- เป็น Binary tree
- Assume ว่าทุก node จบลงที่ Nil Node(All leaf node is Nil)
เงื่อนไข
- Node ใดๆจะเป็นสีแดงไม่ก็ดำ
- Root เป็นสีดำ
- Leaf เป็นสีดำ
- Node ใดเป็น Red Node Child ของ Node นั้นจะต้องเป็น Black Node
- จาก Node u ใดๆทุกๆ Path จาก Node ดังกล่าวไปยัง Leaf ของมันจะต้องมี Node ที่เป็นสีดำเท่ากันทั้งหมด
Lemma
Red-Black tree ที่มี n internal nodes จะมีความสูงไม่เกิน 2log(n+1)
Proof
นิยาม ที่ Node u ใดๆ bh(u) (black height ของ u) จะเท่ากับจำนวน Black Node จาก u ไป Node Leaf ใดๆ(ไม่นับ u))
Claim
สำหรับ internal node u ใดๆจำนวน internal node ใน sub-tree ใดๆที่ u เป็น rootจะมีค่าไม่น้อยกว่า 2^bh(u) -1
Proof (By induction)
ให้ w = u.left และ h = u.right
bh(w) ≥ bh(u) – 1
bh(x) ≥ bh(u) – 1
โดย Induction
Sub-tree ของ w มี internal node ≥ 2^bh(w) -1 ≥ 2^(bh(u)-1) -1
Sub-tree ของ x มี internal node ≥ 2^bh(x) -1 ≥ 2^(bh(u)-1) -1
ดังนั้น internal node ของ u = 1 + 2^(bh(u)-1) -1 + 2^(bh(u)-1) -1 = 2^bh(u) -1
พิจารณา Red-Black Tree ใดๆสูง h
bh(h) ≥ h/2 (เนื่องจาก Red Node จะต้องตามด้วย Black Node เสมอ)
จะได้ Internal node (n)
n ≥ 2^bh(h) -1
n ≥ 2^(h/2)-1
n+1 ≥ 2^(h/2)
log(n+1) ≤ h/2
h ≤2log(n+1)