ผลต่างระหว่างรุ่นของ "204512-53/lecture7"
Kiatchumpol (คุย | มีส่วนร่วม) |
Kiatchumpol (คุย | มีส่วนร่วม) |
||
| (ไม่แสดง 9 รุ่นระหว่างกลางโดยผู้ใช้คนเดียวกัน) | |||
| แถว 77: | แถว 77: | ||
[[ไฟล์:lecture7_figure6.png]] | [[ไฟล์:lecture7_figure6.png]] | ||
| + | |||
| + | '''''Proof:''''' พิจารณาโหนด <math>u</math> ใดๆ ให้ path <math>S=v_0, v_1, v_2, . . ., v_{k-1}, v_k (โดยที่ v_k = u)</math> เป็น shortest path จาก <math>s</math> ไป <math>u</math> | ||
| + | |||
| + | ดังนั้น <math>d(u) = \sum_{i=0}^{k-1} l(v_i, v_{i+1})</math> | ||
| + | |||
| + | เนื่องจาก Ford's algorithm ทำงานจบ เราจะได้ว่า <math>\forall(x,w) \in E</math> , <math>D(x) + l(x,w) \geq D(w)</math> | ||
| + | |||
| + | นั่นคือ <math>l(x,w) \geq D(w) - D(x)</math> | ||
| + | |||
| + | จะได้ว่า <math> d(u) \geq \sum_{i=0}^{k-1} [D(v_{i+1}) - D(v_i) ]</math> | ||
| + | = <math>(D(v_1) - D(v_0)) + (D(v_2) - D(v_1)) + (D(v_3) - D(v_2)) + . . . + (D(v_k) - D(v_{k-1}))</math> | ||
| + | = <math>-D(v_0) + D(v_k) </math> | ||
| + | = <math>D(v_k) </math> (เนื่องจาก<math> D(v_0) = D(s) = 0</math>) | ||
| + | = <math>D(u) </math> (เนื่องจาก <math>D(v_k) = D(u)</math> ) | ||
| + | |||
| + | |||
| + | เมื่อนำ Claim 1 มารวมกับ Claim 2 เราจะสรุปได้ว่า ถ้า Ford's algorithm ทำงานจบ เราจะได้ระยะทาง shortest path | ||
| + | |||
| + | คำถามต่อมาคือ เราจะรู้ได้ยังไงว่า algorithm จะทำงานจนจบ | ||
| + | |||
| + | |||
| + | '''Claim 3:''' ถ้ามี Negative cycle ที่ไปถึงได้จาก <math>s</math> , algorithm จะทำงานไม่จบ | ||
| + | |||
| + | เนื่องจาก labeling step ของ Ford อิงกับเส้นเชื่อมเป็นหลัก ดังนั้นเพื่อให้พิสูจน์ได้ เราจะปรับโครงสร้างสักเล็กน้อย ซึ่งจะอิงกับ node เป็นหลัก พิจารณารูปข้างล่าง | ||
| + | |||
| + | [[ไฟล์:Lecture7_figure7.png]] | ||
| + | |||
| + | แต่ละโหนดจะมี 3 state | ||
| + | |||
| + | - '''''UNLABELED''''' หมายถึง โหนดที่ยังไม่เคยถูกกระทำใดๆ เลย | ||
| + | |||
| + | - '''''LABELED''''' หมายถึง โหนดที่โดน update แล้ว | ||
| + | |||
| + | - '''''SCANNED''''' หมายถึง โหนดที่โดน update แล้ว และได้มีการพิจารณาทุกเส้นเชื่อมที่ติดกับโหนดนั้นและกระจายค่าไปให้คนอื่นแล้ว | ||
| + | |||
| + | |||
| + | '''SCANNING STEP:''' | ||
| + | เลือก labeled node u , scan u แล้วเปลี่ยนสถานะของ u ให้เป็น SCANNED | ||
| + | |||
| + | '''scan (u)''' | ||
| + | for all edge(u,v) | ||
| + | if D(u) + l(u,v) < D(v) | ||
| + | D(v) <- D(u) + l(u,v) | ||
| + | p(v) <- u | ||
| + | เปลี่ยนสถานะ v ให้เป็น LABELED | ||
| + | |||
| + | ดูตัวอย่างตามรูปข้างล่าง | ||
| + | มีกราฟ | ||
| + | [[ไฟล์:lecture7_figure8.png]] | ||
| + | |||
| + | เริ่มต้น | ||
| + | [[ไฟล์:lecture7_figure9.png]] | ||
| + | |||
| + | เมื่ออัลกอริทึมเริ่มทำงาน ตามรูป โหนด s มีสถานะเป็น scanned ส่วนโหนด a มีสถานะเป็น labeled | ||
| + | [[ไฟล์:lecture7_figure10.png]] | ||
| + | |||
| + | ถ้ามีการ update โหนดที่เป็น scanned อยู่แล้ว โหนดนั้นก็จะกลับมาสู่สถานะ labeled อีกครั้ง | ||
| + | |||
| + | เมื่อทุกโหนดเปลี่ยนสถานะเป็น scanned ทั้งหมด อัลกอรึทึมนี้ก็จะถือว่าทำงานจบ | ||
| + | [[ไฟล์:lecture7_figure11.png]] | ||
| + | |||
| + | จะเห็นว่า มีความเป็นไปได้ที่เราจะต้องทำการ scan โหนดบางโหนดมากกว่าหนึ่งครั้ง ดังนั้นถ้าเราสามารถจัดลำดับของการ scan ที่ทำให้แต่ละโหนดได้รับการ scan แค่ครั้งเดียวก็จะเป็นการดี | ||
| + | |||
| + | '''Directed Acyclic Graph (DAG)''' | ||
| + | |||
| + | กราฟที่มีทิศทาง G จะเป็น DAG ก็ต่อเมื่อ G ไม่มี cycle | ||
| + | |||
| + | ให้กราฟ <math>G</math> , ลำดับของโหนด <math>v_1, v_2, v_3, ..., v_n</math> จะเป็น topological order ถ้าไม่มีเส้นเชื่อม <math>(v_i, v_j)</math> ที่ <math>i > j</math> | ||
| + | |||
| + | ถ้ากราฟใดๆ มี topological order ก็สรุปได้ว่าเราสามารถไล่ scan โหนดไปในทิศทางเดียวโดยที่ไม่ต้องย้อนกลับมา scan โหนดเดิมอีกได้ | ||
| + | |||
| + | รูปข้างล่างแสดงตัวอย่างของกราฟที่ไม่มี topological order | ||
| + | |||
| + | [[ไฟล์:lecture7_figure12.png]] | ||
| + | |||
| + | นั่นคือ ถ้ากราฟมี cycle กราฟนั้นจะไม่มี topological order | ||
| + | |||
| + | '''คำถาม''' ถ้ากราฟไม่มี cycle กราฟนั้นจะมี topological order รึเปล่า | ||
| + | |||
| + | '''ตอบ''' มีเสมอ สามารถพิสูจน์ได้โดยแสดงอัลกอริทึม topological sort | ||
| + | |||
| + | Topological Sort | ||
| + | - โหนดที่ไม่มี edge ใดๆ ชี้หาเรียกว่า "source" | ||
| + | - วิธีการคือ วิ่งหา source แล้วก็ลบโหนดนั้นทิ้ง แล้วก็ไล่หา source ตัวถัดไปแล้วก็ลบโหนดนั้นทิ้งอีก ทำเช่นนี้ไปเรื่อยๆ ลำดับในการลบที่ได้คือ topological order | ||
| + | |||
| + | พิสูจน์ว่า DAG ใดๆ มี topological order โดยใช้วิธีการ contradiction | ||
| + | เนื่องจากกราฟมีโหนดจำนวนจำกัด ถ้าหากอัลกอริทึม topological sort สามารถทำงานไปได้เรื่อยๆ ไม่จบ แสดงว่ากราฟนั้นมี cycle ซึ่งไม่เป็น DAG | ||
| + | |||
| + | |||
| + | '''Dijkstra's Algorithm''' ''ใช้กับกราฟที่ไม่มี negative cycle'' | ||
| + | |||
| + | เป็นวิธีการแบบหนึ่งที่ใช้สำหรับหา shortest path โดยใช้หลักการ <u>เลือกสแกน labeled node u ที่มี <math>D(u)</math> น้อยที่สุด</u> ซึ่งทำให้รับประกันได้ว่าเมื่อเราสแกนโหนดนี้ไปแล้วจะไม่ต้องกลับมาสแกนที่โหนดเดียวกันอีก | ||
| + | |||
| + | <math> algorithm:</math><br><br> | ||
| + | :<math> S \leftarrow \emptyset</math><br> | ||
| + | :<math> D(u) \leftarrow \infty , for all u</math><br> | ||
| + | :<math> D(s) \leftarrow 0</math><br> | ||
| + | :<math> while s \neq v do</math><br> | ||
| + | :: เลือก <math>u \isin S</math> ที่มีค่า <math>D(u) </math> น้อยที่สุด _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ ขั้นตอนนี้เรียกว่าการทำ Extract Min<br> | ||
| + | ::<math> scan(u)</math><br> | ||
| + | ::<math> S \leftarrow S \cup {u}</math><br> | ||
| + | |||
| + | |||
| + | |||
| + | <math>scan(u): </math><br> | ||
| + | : <math>for</math> <math>all</math> <math>edge(u,v)</math><br> | ||
| + | :<math> if D(u) + l(u,v) < D(v)</math><br> | ||
| + | ::<math> D(v) \leftarrow D(u) + l(u,v)</math> _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ ขั้นตอนนี้เรียกว่าการทำ Decrease Key<br> | ||
| + | ::<math> p(v) \leftarrow u</math><br> | ||
| + | :: เปลี่ยนสถานะ <math>v</math> ให้เป็น Labeled | ||
| + | |||
| + | |||
| + | Data structure ที่เหมาะนำมาใช้กับ algorithm นี้คือ priority queue , ถ้ามี priority queue ที่สามารถ <br> | ||
| + | :* Extract Min ได้ในเวลา <math>\alpha</math> <br> | ||
| + | :* Decrease Key ได้ในเวลา <math>\beta</math> <br> | ||
| + | ดังนั้น เมื่อวิเคราะห์เวลาการทำงานของ Dijkstra's algorithm จะได้ว่า algorithm ทำงานในเวลา <math>O(n * \alpha + m * \beta)</math> | ||
| + | |||
| + | เมื่อวิเคราะห์เวลาการทำงานของ Dijkstra's algorithm เมื่อใช้ data structure แบบอื่นๆ จะได้ตามตารางข้างล่าง | ||
| + | |||
| + | |||
| + | {|border="1" width="600" | ||
| + | | <center>Data Structure</center>|| <center><math>\alpha</math></center> || <center><math>\beta</math></center> || <center>Dijkstra</center> | ||
| + | |- | ||
| + | | Array || <math>O(n)</math> || <math>O(1)</math> || <math>O(n^2)</math> | ||
| + | |- | ||
| + | | Heap || <math>O(log n)</math> || <math>O(log n)</math> || <math>O((m+n) log n)</math> | ||
| + | |- | ||
| + | | Fibonacci Heap || <math>O(log n)</math> || <math>O(1)</math><br>amortized || <math>O(nlogn+m)</math> | ||
| + | |} | ||
| + | |||
| + | |||
| + | '''General Case''' (general weights) <br> | ||
| + | : '''Bellman-Ford-Moore''' <br> | ||
| + | : <math>While</math> <math>True</math> <br> | ||
| + | :: <math>for</math> <math>all</math> <math>node</math> <math>u</math> <math>\isin</math> <math>V</math> <br> | ||
| + | ::: <math>scan(u)</math> <br> | ||
| + | |||
| + | <u>'''Claim'''</u><br> | ||
| + | หลังการทำงานของ BFM ไป i รอบ โหนด <math>u</math> ที่มี shortest path จาก <math>u</math> ไป <math>s</math> ไม่เกิน i เส้น จะมี <math>D(u) = d(v)</math> | ||
| + | |||
| + | <u>'''Thm'''</u><br> | ||
| + | ถ้ากราฟไม่มี negative cycle, BFM จะทำงานไม่เกิน n-1 รอบ | ||
| + | |||
| + | ดังนั้น BFM ทำงานในเวลา <math>O(nm)</math> | ||
รุ่นแก้ไขปัจจุบันเมื่อ 10:54, 23 กันยายน 2553
จดบันทึกคำบรรยายโดย:
5314550032 นาย กิตติกานต์ ดวงประภา
5314550041 นาย เกียรติชุมพล สุทธิศิริกุล
5314550059 นาย ฉนานนท์ ตันสกุล
Shortest Paths
มี โดยที่
มี : โดยที่
ให้ สำหรับ ใดๆ แทนระยะทางที่สั้นที่สุดจาก ไป
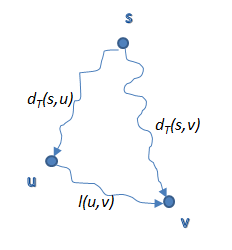
Lemma: ถ้าให้ เป็นระยะทางจาก ไป บน แล้ว จะเป็น shortest path tree ก็ต่อเมื่อ(if and only if) สำหรับทุกๆ เส้นเชื่อม
พิจารณาตัวอย่าง
จากรูปข้างบน ในที่นี้ ไม่ใช่ shortest path แล้ว ถ้าเราอยากทราบ shortest path เราก็บอก parent ของ ให้วิ่งไปหา shortest path ทางอื่น อย่าวิ่งผ่านมาที่ (นี่คือการ update shortest path)
Framework ของการหา shortest path
- ทุกๆ โหนดเก็บ parent , โหนด เก็บ ที่เป็น parent ใน candidate shortest path tree
(เริ่มต้น)
- ทุกๆ โหนด เก็บ ซึ่งแทนระยะทางที่สั้นที่สุด"เท่าที่ทราบ" จาก ไป
(เริ่มต้น)
LABELING STEP:
เลือกเส้นเชื่อม ที่ จากนั้น
Ford's algorithm -> ทำ labeling step ไปเรื่อยๆ
ตัวอย่าง
Step เริ่มต้น และ ของโหนดอื่นๆ มีค่าเป็น
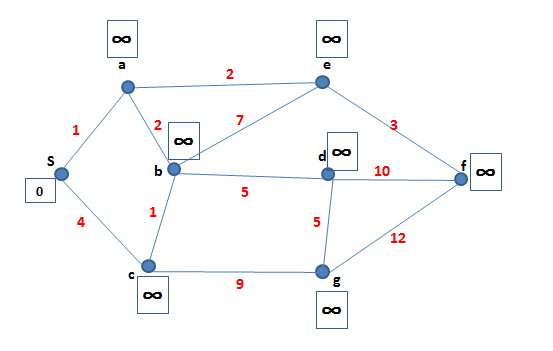
Step ต่อมา ค่อยๆ ปรับ และ parent (หัวลูกศรชี้หา parent)
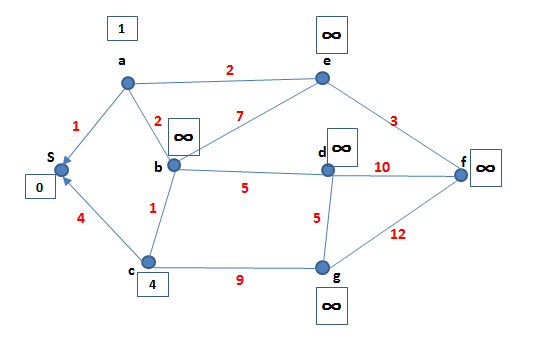
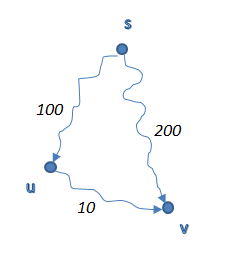
Claim 1: ถ้า , จะมี path จาก ไป ที่มีความยาว
Claim 2: ถ้า Ford's Algorithm ทำงานจบ, ระยะทางที่สั้นที่สุดจาก ไป
(นั่นคือ ระยะที่ estimate ได้ จะไม่มากไปกว่าระยะทางที่สั้นที่สุด)
ถ้า algorithm ทำงานจบ เราจะรู้ว่า
Proof: พิจารณาโหนด ใดๆ ให้ path เป็น shortest path จาก ไป
ดังนั้น
เนื่องจาก Ford's algorithm ทำงานจบ เราจะได้ว่า ,
นั่นคือ
จะได้ว่า
=
=
= (เนื่องจาก)
= (เนื่องจาก )
เมื่อนำ Claim 1 มารวมกับ Claim 2 เราจะสรุปได้ว่า ถ้า Ford's algorithm ทำงานจบ เราจะได้ระยะทาง shortest path
คำถามต่อมาคือ เราจะรู้ได้ยังไงว่า algorithm จะทำงานจนจบ
Claim 3: ถ้ามี Negative cycle ที่ไปถึงได้จาก , algorithm จะทำงานไม่จบ
เนื่องจาก labeling step ของ Ford อิงกับเส้นเชื่อมเป็นหลัก ดังนั้นเพื่อให้พิสูจน์ได้ เราจะปรับโครงสร้างสักเล็กน้อย ซึ่งจะอิงกับ node เป็นหลัก พิจารณารูปข้างล่าง
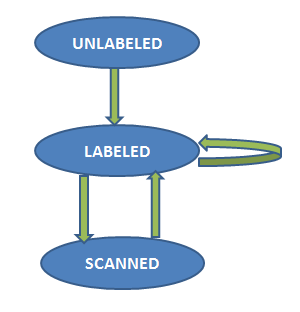
แต่ละโหนดจะมี 3 state
- UNLABELED หมายถึง โหนดที่ยังไม่เคยถูกกระทำใดๆ เลย
- LABELED หมายถึง โหนดที่โดน update แล้ว
- SCANNED หมายถึง โหนดที่โดน update แล้ว และได้มีการพิจารณาทุกเส้นเชื่อมที่ติดกับโหนดนั้นและกระจายค่าไปให้คนอื่นแล้ว
SCANNING STEP:
เลือก labeled node u , scan u แล้วเปลี่ยนสถานะของ u ให้เป็น SCANNED
scan (u)
for all edge(u,v)
if D(u) + l(u,v) < D(v)
D(v) <- D(u) + l(u,v)
p(v) <- u
เปลี่ยนสถานะ v ให้เป็น LABELED
ดูตัวอย่างตามรูปข้างล่าง
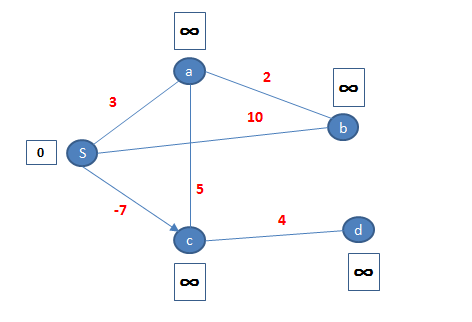
มีกราฟ
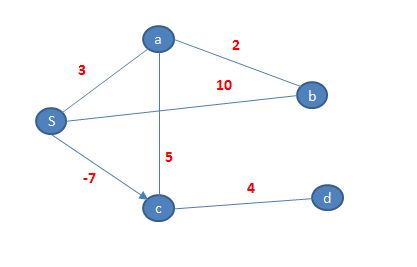
เมื่ออัลกอริทึมเริ่มทำงาน ตามรูป โหนด s มีสถานะเป็น scanned ส่วนโหนด a มีสถานะเป็น labeled
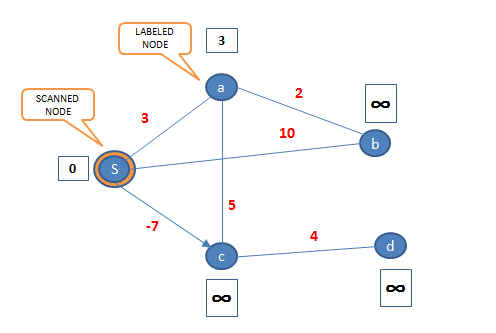
ถ้ามีการ update โหนดที่เป็น scanned อยู่แล้ว โหนดนั้นก็จะกลับมาสู่สถานะ labeled อีกครั้ง
เมื่อทุกโหนดเปลี่ยนสถานะเป็น scanned ทั้งหมด อัลกอรึทึมนี้ก็จะถือว่าทำงานจบ
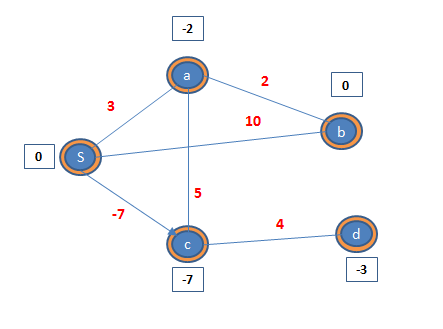
จะเห็นว่า มีความเป็นไปได้ที่เราจะต้องทำการ scan โหนดบางโหนดมากกว่าหนึ่งครั้ง ดังนั้นถ้าเราสามารถจัดลำดับของการ scan ที่ทำให้แต่ละโหนดได้รับการ scan แค่ครั้งเดียวก็จะเป็นการดี
Directed Acyclic Graph (DAG)
กราฟที่มีทิศทาง G จะเป็น DAG ก็ต่อเมื่อ G ไม่มี cycle
ให้กราฟ , ลำดับของโหนด จะเป็น topological order ถ้าไม่มีเส้นเชื่อม ที่
ถ้ากราฟใดๆ มี topological order ก็สรุปได้ว่าเราสามารถไล่ scan โหนดไปในทิศทางเดียวโดยที่ไม่ต้องย้อนกลับมา scan โหนดเดิมอีกได้
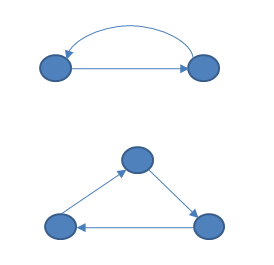
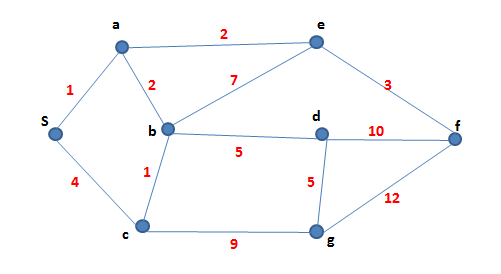
รูปข้างล่างแสดงตัวอย่างของกราฟที่ไม่มี topological order
นั่นคือ ถ้ากราฟมี cycle กราฟนั้นจะไม่มี topological order
คำถาม ถ้ากราฟไม่มี cycle กราฟนั้นจะมี topological order รึเปล่า
ตอบ มีเสมอ สามารถพิสูจน์ได้โดยแสดงอัลกอริทึม topological sort
Topological Sort - โหนดที่ไม่มี edge ใดๆ ชี้หาเรียกว่า "source" - วิธีการคือ วิ่งหา source แล้วก็ลบโหนดนั้นทิ้ง แล้วก็ไล่หา source ตัวถัดไปแล้วก็ลบโหนดนั้นทิ้งอีก ทำเช่นนี้ไปเรื่อยๆ ลำดับในการลบที่ได้คือ topological order
พิสูจน์ว่า DAG ใดๆ มี topological order โดยใช้วิธีการ contradiction
เนื่องจากกราฟมีโหนดจำนวนจำกัด ถ้าหากอัลกอริทึม topological sort สามารถทำงานไปได้เรื่อยๆ ไม่จบ แสดงว่ากราฟนั้นมี cycle ซึ่งไม่เป็น DAG
Dijkstra's Algorithm ใช้กับกราฟที่ไม่มี negative cycle
เป็นวิธีการแบบหนึ่งที่ใช้สำหรับหา shortest path โดยใช้หลักการ เลือกสแกน labeled node u ที่มี น้อยที่สุด ซึ่งทำให้รับประกันได้ว่าเมื่อเราสแกนโหนดนี้ไปแล้วจะไม่ต้องกลับมาสแกนที่โหนดเดียวกันอีก
- เลือก ที่มีค่า น้อยที่สุด _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ ขั้นตอนนี้เรียกว่าการทำ Extract Min
- เลือก ที่มีค่า น้อยที่สุด _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ ขั้นตอนนี้เรียกว่าการทำ Extract Min
-
- _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ ขั้นตอนนี้เรียกว่าการทำ Decrease Key
- เปลี่ยนสถานะ ให้เป็น Labeled
- _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ ขั้นตอนนี้เรียกว่าการทำ Decrease Key
Data structure ที่เหมาะนำมาใช้กับ algorithm นี้คือ priority queue , ถ้ามี priority queue ที่สามารถ
- Extract Min ได้ในเวลา
- Decrease Key ได้ในเวลา
- Extract Min ได้ในเวลา
ดังนั้น เมื่อวิเคราะห์เวลาการทำงานของ Dijkstra's algorithm จะได้ว่า algorithm ทำงานในเวลา
เมื่อวิเคราะห์เวลาการทำงานของ Dijkstra's algorithm เมื่อใช้ data structure แบบอื่นๆ จะได้ตามตารางข้างล่าง
| Array | |||
| Heap | |||
| Fibonacci Heap | amortized |
General Case (general weights)
- Bellman-Ford-Moore
-
-
Claim
หลังการทำงานของ BFM ไป i รอบ โหนด ที่มี shortest path จาก ไป ไม่เกิน i เส้น จะมี
Thm
ถ้ากราฟไม่มี negative cycle, BFM จะทำงานไม่เกิน n-1 รอบ
ดังนั้น BFM ทำงานในเวลา




















![{\displaystyle d(u)\geq \sum _{i=0}^{k-1}[D(v_{i+1})-D(v_{i})]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f902039d002fc3fb23e7f5c6fb8dde33b714dcb9)