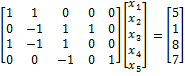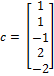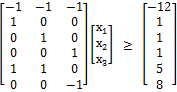ผลต่างระหว่างรุ่นของ "204512/บรรยาย 10"
Jittat (คุย | มีส่วนร่วม) (ย้อน) |
|||
| (ไม่แสดง 5 รุ่นระหว่างกลางโดยผู้ใช้ 4 คน) | |||
| แถว 18: | แถว 18: | ||
---- | ---- | ||
=== <u>Linear Programming Problem</u> === | === <u>Linear Programming Problem</u> === | ||
| − | Instant ของ linear programming คือ จำนวนเต็มบวก n, m เวกเตอร์ c ∈ R | + | Instant ของ linear programming คือ จำนวนเต็มบวก n, m เวกเตอร์ c ∈ R<sup>n</sup>, b ∈ R<sup>m</sup> และเมตริกซ์ A ของจำนวนจริงขนาด m x n จะได้ว่า |
| − | :F = { x ∈ R | + | :F = { x ∈ R<sup>n</sup> :Ax = b , x ≥0 } |
:Cost : x → c'x | :Cost : x → c'x | ||
| แถว 120: | แถว 120: | ||
::minimize: [[ภาพ:Image019.png]]<br> | ::minimize: [[ภาพ:Image019.png]]<br> | ||
::subject to: | ::subject to: | ||
| − | ::: | + | :::<math>t_i</math> ≥ <math>d_i</math> ; i = 1, … ,12 |
| − | ::: | + | :::<math>k_i</math> = <math>t_i</math> - <math>d_i</math> ; i = 1, … ,12 |
| − | ::: | + | :::<math>t_i</math> – <math>t_i</math>-1 ≤ <math>b_i</math> |
| − | ::: | + | :::<math>b_i</math> ≥ 0 ; i = 1, … ,12 |
| − | ::: | + | :::<math>t_i</math>-1 – <math>t_i</math> ≤ <math>s_i</math> |
| − | ::: | + | :::<math>s_i</math> ≥ 0 |
| − | ::: | + | :::<math>t_i</math> ≥ 0 |
| − | '''''Note''''' maximize เป็นส่วนกลับของ minimize สามารถแปลงกลับไปมาได้โดยเอา -1 | + | '''''Note''''' maximize เป็นส่วนกลับของ minimize สามารถแปลงกลับไปมาได้โดยเอา -1 คูณเงื่อนไข |
---- | ---- | ||
รุ่นแก้ไขปัจจุบันเมื่อ 11:10, 23 กันยายน 2553
จดบันทึกคำบรรยายโดย:
- นายณัฐพล หล่อศิริ 50653781 และ
- นายวรวุทธ นัมคนิสรณ์ 50653898
- นายณัฐพล หล่อศิริ 50653781 และ
Linear Programming
Note Problem ต่างจาก Instant ของ Problem กล่าวคือ Problem จะเท่ากับ เซตของ Instant ของ Problem
Note ตัวแปรทั้งหมดเป็นตัวแปรแบบเวกเตอร์ เพราะฉะนั้นจะขอละ ไม่ใส่เครื่องหมายเวกเตอร์
Optimization Problem
Instant ของปัญหา Optimization Problem จะประกอบด้วย
- set F (เซตของคำตอบที่เป็นไปได้)
- function cost F→R (จำนวนจริง)
ต้องการหา f∈F และ cost (f) ≤ cost (y) , สำหรับทุกๆ y∈F
Linear Programming Problem
Instant ของ linear programming คือ จำนวนเต็มบวก n, m เวกเตอร์ c ∈ Rn, b ∈ Rm และเมตริกซ์ A ของจำนวนจริงขนาด m x n จะได้ว่า
- F = { x ∈ Rn :Ax = b , x ≥0 }
- Cost : x → c'x
- ตัวอย่าง
กำหนดให้ n = 3, m = 1
เขียนเป็นเมตริกซ์ ได้เป็น
- ตัวอย่าง
- การเขียนในรูปแบบ สมการ
- - การระบุเซต F (เป็น constraint ของปัญหา)
- + = 5
- + – = 1
- - + = 8
- – = 7
- ≥ 0 ทุกๆ 1 ≤ i ≤5
- - การระบุ c (เป็น objective ของปัญหา)
- minimize: + – + –
- การเขียนในรูปแบบ เมตริกซ์
Form ของ Linear Programming
Standard form
- เมตริกซ์
- minimize: cx
- subject to: Ax = b ; x ≥ 0
Canonical form
- เมตริกซ์
- minimize: cx
- subject to: Ax ≥ b ; x ≥ 0
- ตัวอย่าง
- เตรียมสอบมีเวลาอ่านหนังสือ 12 ชม. มี 3 วิชา Architect, Algo, Soft Com. อ่านอย่างน้อยวิชาละ 1 ชม., อ่าน architect & algo รวมกันไม่น้อยกว่า 5 ชม., อ่าน Soft Com. ไม่เกิน 8 ชม.
ถ้าให้
- = เวลาอ่าน Architect
- = เวลาอ่าน Algo
- = เวลาอ่าน Soft Com.
ให้ความเหนื่อยในการอ่านเป็น + 5 + 2
เป้าหมายคือ ต้องการอ่านหนังสือให้ได้ตามเงื่อนไข + ความเหนื่อยน้อยสุด
วิธีทำ
- minimize: + 5 + 2
- subject to:
- + + ≤ 12
- ≥ 1
- ≥ 1
- ≥ 1
- + ≥ 5
- ≤ 8
- , , ≥ 0
แปลงให้อยู่ในรูป canonical form การทำให้สมการที่เป็น ≤ ให้เป็น ≥ ให้หมดจะได้ว่า
- minimize: + 5 + 2
- subject to:
- จาก + + ≤ 12 เอา -1 คูณตลอดจะได้
- + + ≥ -12
- จาก ≤ 8 เอา -1 คูณตลอดจะได้
- ≥ -8
- ≥ 1
- ≥ 1
- ≥ 1
- + ≥ 5
- , , ≥ 0
เขียนเป็น matrix ได้
- ตัวอย่าง
- บริษัทเช่าเต๊นท์มหาสนุกจำกัด รับจัดหาเต็นท์ในเดือนๆหนึ่งมีเต็นท์ใช้ได้ไม่น้อยกว่าจำนวนที่ใช้ โดยมีเงื่อนไขว่าเต็นท์ซื้อขายได้ เก็บเต็นท์ในโกดังคิดค่าเช่าโกดัง จะซื้อขายหรือเก็บเต็นท์ยังไงให้ได้กำไรมากที่สุด
- กำหนด
- ; i = 1, … ,12 เป็นจำนวนเต๊นท์ที่ต้องการในเดือนที่ i
- ; เป็นจำนวนเต๊นท์ที่เหลือจากปีที่แล้ว
- ; ราคาซื้อเต๊นท์ / เต๊นท์
- ; ราคาขายเต๊นท์ / เต๊นท์
- ; ราคาเก็บเต๊นท์ที่ไม่ได้ใช้ / เดือน
- ตัวแปร
- , … , จำนวนเต๊นท์ที่เราครอบครองในเดือนที่ i
- , … , จำนวนเต๊นท์ที่ซื้อในเดือนที่ i
- , … , จำนวนเต๊นท์ที่ขายในเดือนที่ i
- , … , จำนวนเต๊นท์ในโกดังในเดือนที่ i
- จะได้ว่า
Note maximize เป็นส่วนกลับของ minimize สามารถแปลงกลับไปมาได้โดยเอา -1 คูณเงื่อนไข
Shortest path in Linear Programming
- ตัวอย่าง
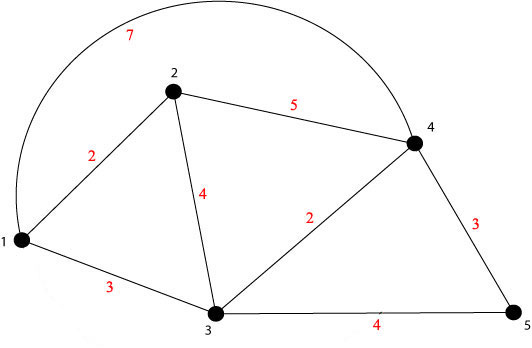
สมมติ path ดังรูป d1 = 0, ตัวแปร d1, … , d5 แทนระยะสั้นสุดจาก node 1 ไปยัง node ต่างๆ
ให้กราฟแบบมีทิศทาง G = (V,E) ความยาว l บนเส้นเชื่อม, จุดเริ่มต้น s∈V
ให้ dv แทนระยะสั้นสุดจาก s ไป v สำหรับ v∈V
จะได้ว่า
Integer Programming
- คือการบอกว่า constraint (subject to) มีการกำหนดให้เป็นจำนวนเต็มค่าใดค่าหนึ่ง
Assignment Problem
- ตัวอย่าง
- มีคน n คน มีงาน n งาน
- คนที่ i ทำงาน j ใช้เวลา w_ij หน่วย
วิธีทำ
Duality
- ตัวอย่าง
- minimize: 7x1 + x2 + 5x3
- subject to:
- x1 – x2 + 3x3 ≥ 10 …(1)
- 5x1 + 2x2 – x3 ≥ 6 …(2)
- x1, x2, x3 ≥ 0
- ค่า objective ของคำตอบที่ดีที่สุด = Z*
- สมมติ
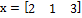 แล้วบอกได้ว่า Z* ≤ 30
แล้วบอกได้ว่า Z* ≤ 30 - (1)x 2 + (2); 7x1 + 5x3 ≥ 26
- สังเกตว่าคล้ายๆ minimize เพราะฉะนั้นบอกได้ว่า lower bound เป็น 26
- (1)x y1 → y1x1 – y1x2 + 3y1x3 ≥ 10y1
- (2)x y2 → 5y2x1 + 2y2x2 – y2x3 ≥ 6y2
- ต้องการ สัมประสิทธิ์ของ x1 = 7, สัมประสิทธิ์ของ x2 = 1, สัมประสิทธิ์ของ x3 = 5
- เพราะฉะนั้นจะสร้าง linear program ได้อีกอันว่า
- maximize: 10y1 + 6y2
- subject to:
- y1 + 5y2 ≤ 7 …(3)
- -y1 + 2y2 ≤ 1 …(4)
- 3y1 - y2 ≤ 5 …(5)
- y1, y2 ≥ 0
- ค่า objective ของคำตอบที่ดีที่สุด = A*
- เพราะฉะนั้น A* = Z* จะเรียกว่า strong duality
- โดย
- สมการที่ (1), (2) จะเรียกว่า Primal
- สมการที่ (3), (4), (5) จะเรียกว่า Dual
Primal Linear Programming
Dual Linear Programming
Max flow & Min Cut
ให้ P แทนเซตของ simple path ทั้งหมดจาก s ไป t สำหรับ path p∈P มี ตัวแปร fp แทนปริมาณ flow ใน path นั้น
- ดังนั้นสรุปได้ว่า Min Cut เป็น Dual ของ Max Flow
- ตัวอย่าง
- primal
- minimize: 2x1 + 5x2
- subject to:
- x1 + x2 ≥ 5 …y1
- -x1 + x2 ≥ -1 …y2
- x1 + 2x2 ≥ 4 …y3
- x1, x2 ≥ 0
- แปลงเป็น dual ได้ว่า
- dual
- maximize: 5y1 – y2 + 4y3
- subject to:
- y1 – y2 + y3 ≤ 2
- y1 + y2 + 2y3 ≤ 5
- y1, y2, y3 ≥ 0