ผลต่างระหว่างรุ่นของ "204512-53/lecture8"
Poipy (คุย | มีส่วนร่วม) |
|||
| (ไม่แสดง 10 รุ่นระหว่างกลางโดยผู้ใช้ 3 คน) | |||
| แถว 1: | แถว 1: | ||
| + | {{หัวคำบรรยาย|204512-53}} | ||
| + | Algorithm Lecture #8 | ||
'''จดบันทึกคำบรรยายโดย:''' | '''จดบันทึกคำบรรยายโดย:''' | ||
| − | นาย | + | |
| − | นาย | + | นาย บดินทร์ แสงทองล้วน 5314550113 |
| − | นาย | + | |
| + | นาย วิชา มีสุขสบาย 5314550164 | ||
| + | |||
| + | นาย อภิชาติ ทวีศิริเวทย์ 5314550199 | ||
| + | |||
---- | ---- | ||
| + | |||
| + | =Network flow problem= | ||
| + | |||
| + | 1. กราฟมีทิศทาง | ||
| + | |||
| + | 2. ความจุ (capacity) <math>\ c : E \rightarrow \mathbb{R+}</math> | ||
| + | |||
| + | 3. จุดเริ่มต้น source <math>\ s \in V</math> | ||
| + | |||
| + | 4. จุดสิ้นสุด sink <math>\ t \in V</math> | ||
| + | |||
| + | 5. flow เป็น function จาก <math>V \times V \rightarrow \mathbb{R}</math> | ||
| + | |||
| + | เงื่อนไข | ||
| + | |||
| + | 1. Capacity constraints : <math>\ f \le c(u,v)</math> | ||
| + | |||
| + | 2. Skew symmetry : <math>\ f(u,v) = - f(v,u)</math> | ||
| + | |||
| + | 3. conservation : <math>\ \sum_{V} f(u,v) = 0</math> | ||
| + | |||
| + | ปริมาตร flow <math> |f| = \ \sum_{V} f(u,v) = 0</math> | ||
=Maximum flow problem= | =Maximum flow problem= | ||
| แถว 12: | แถว 40: | ||
G คือ กราฟที่เราสนใจ | G คือ กราฟที่เราสนใจ | ||
| + | |||
G = (V,E) คือ ฟังก์ชั่นของกราฟ G โดยที่ V คือ เซตของโหนด และ E คือเซตของเส้นเชื่อม | G = (V,E) คือ ฟังก์ชั่นของกราฟ G โดยที่ V คือ เซตของโหนด และ E คือเซตของเส้นเชื่อม | ||
| + | |||
C: E->R+ คือ Capacity ของเส้นเชื่อม เซตจำนวนจริงบวกไม่รวมศูนย์ (0, +∞) | C: E->R+ คือ Capacity ของเส้นเชื่อม เซตจำนวนจริงบวกไม่รวมศูนย์ (0, +∞) | ||
| + | |||
s-t คือ เซตของเส้นทางจาก s ไปถึง t | s-t คือ เซตของเส้นทางจาก s ไปถึง t | ||
| แถว 19: | แถว 50: | ||
=Classic problem= | =Classic problem= | ||
| + | |||
| + | [[ไฟล์:Untitled1.png ]] | ||
| + | |||
| + | Maximum flow คือเท่าไหร่ : ต้องหา path มาเรื่อยๆ จนไม่มี path | ||
| + | |||
| + | [[ไฟล์:Untitled2.png]] หรือ [[ไฟล์:Untitled3.png]] | ||
| + | |||
| + | ถ้าได้รูปแบบข้างต้นก็ไม่มีปัญหา แต่ถ้าเกิดได้แบบ | ||
| + | |||
| + | [[ไฟล์:Untitled4.png]] | ||
| + | |||
| + | จะกลายเป็นปัญหา แล้วจะแก้ไขอย่างไร? | ||
| + | |||
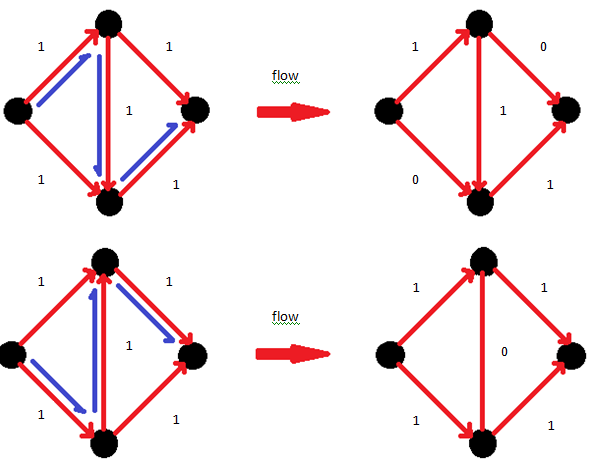
| + | แนวคิด | ||
| + | |||
| + | [[ไฟล์:Untitled5.png]] | ||
| + | |||
| + | [[ไฟล์:Untitled6.png]] | ||
| + | |||
| + | [[ไฟล์:Untitled7.png]] | ||
| + | |||
| + | Algorithm | ||
| + | :# F <- 0 | ||
| + | :# G(f) เป็น residual graph ของ f | ||
| + | :# ถ้ามี path จาก s ไป t ใน G(f) | ||
| + | :# P <- path จาก s ไป t ใน G(f) | ||
| + | :# C <- capacity ต่ำสุดของเส้นเชื่อมใน path P | ||
| + | :# Update f ด้วย flow path P ด้วยปริมาตร C | ||
| + | :# หา G(f) <- residual graph ของ flow f | ||
| + | |||
=st-cut= | =st-cut= | ||
| แถว 24: | แถว 85: | ||
พิจารณา sub set ของ node กลุ่มหนึ่ง | พิจารณา sub set ของ node กลุ่มหนึ่ง | ||
| + | [[ไฟล์:St_1.png]] | ||
ถ้า <math> s \in S ,t \notin S </math> จะเรียก <math>(S,\bar S)</math> ว่า st-cut ; | ถ้า <math> s \in S ,t \notin S </math> จะเรียก <math>(S,\bar S)</math> ว่า st-cut ; | ||
| แถว 44: | แถว 106: | ||
S</math> ทั้งหมดเลย | S</math> ทั้งหมดเลย | ||
| + | |||
| + | [[ไฟล์:St_2.png]] | ||
| + | |||
| + | flow สามารถวิ่งไปและวิ่่งกลับได้ | ||
สำหรับ st-cut ใดๆ เราได้ว่า | สำหรับ st-cut ใดๆ เราได้ว่า | ||
| แถว 58: | แถว 124: | ||
พิสูจน์ | พิสูจน์ | ||
| + | |||
| + | [[ไฟล์:St_3.png]] | ||
<math>{S}=S_0 \supset S_1 \supset S_2 \supset S_3 \subset S_4 \subset \ldots \subset | <math>{S}=S_0 \supset S_1 \supset S_2 \supset S_3 \subset S_4 \subset \ldots \subset | ||
| แถว 66: | แถว 134: | ||
พิสูจน์ โดย Induction ตั้งแต่ 0 ถึง k | พิสูจน์ โดย Induction ตั้งแต่ 0 ถึง k | ||
| + | |||
| + | [[ไฟล์:St_4.png]] | ||
<math>f(S_0,\bar S_0) = |f|</math> เป็น base case ซึ่งจะเท่ากันตามนิยาม | <math>f(S_0,\bar S_0) = |f|</math> เป็น base case ซึ่งจะเท่ากันตามนิยาม | ||
| แถว 72: | แถว 142: | ||
<math>f(S_{i+1},\bar S_{i+1}) = |f|</math> | <math>f(S_{i+1},\bar S_{i+1}) = |f|</math> | ||
| + | |||
| + | [[ไฟล์:St_5.png]] | ||
ได้ <math>S_i</math> มี flow ที่วิ่งเข้าวิ่งออกของ c กับ d สุดท้ายรวม flow เส้นปะเข้า | ได้ <math>S_i</math> มี flow ที่วิ่งเข้าวิ่งออกของ c กับ d สุดท้ายรวม flow เส้นปะเข้า | ||
| แถว 114: | แถว 186: | ||
หา s-t cut <math>(S^*,\bar S^*)</math> ที่ <math>Cap(S^*,\bar S^*)</math> | หา s-t cut <math>(S^*,\bar S^*)</math> ที่ <math>Cap(S^*,\bar S^*)</math> | ||
| + | |||
| + | [[ไฟล์:St_6.png]] | ||
เราต้องการ <math>|f|= f(S^*,\bar S^*) = Cap(S^*,\bar S^*)</math> | เราต้องการ <math>|f|= f(S^*,\bar S^*) = Cap(S^*,\bar S^*)</math> | ||
| แถว 124: | แถว 198: | ||
เราพิสูจน์โดย By Contradition | เราพิสูจน์โดย By Contradition | ||
| + | |||
| + | [[ไฟล์:St_7.png]] | ||
พิจารณา e=(u,v) ที่ <math>u \in S^*;v \in \bar S^*</math> | พิจารณา e=(u,v) ที่ <math>u \in S^*;v \in \bar S^*</math> | ||
| แถว 134: | แถว 210: | ||
สิ่งที่เราได้นอกจากจะได้ max flow เราจะได้ min cut เพราะ max flow = min cap | สิ่งที่เราได้นอกจากจะได้ max flow เราจะได้ min cut เพราะ max flow = min cap | ||
| + | |||
| + | [[ไฟล์:St_8.png]] | ||
==เวลาในการทำงาน== | ==เวลาในการทำงาน== | ||
| แถว 144: | แถว 222: | ||
ตัวอย่างที่ Fold-Fullerson ล้มเหลว | ตัวอย่างที่ Fold-Fullerson ล้มเหลว | ||
| + | |||
| + | [[ไฟล์:St_9.png]] | ||
==Bipatite Matching== | ==Bipatite Matching== | ||
| แถว 156: | แถว 236: | ||
เซต <math> M \subseteq E </math> เรียกว่าเป็น matching ถ้าไม่มีโหนดใดๆ ติดกับเส้นเชื่อม M เกิน 1 เส้น | เซต <math> M \subseteq E </math> เรียกว่าเป็น matching ถ้าไม่มีโหนดใดๆ ติดกับเส้นเชื่อม M เกิน 1 เส้น | ||
| + | |||
| + | [[ไฟล์:St_10.png]] | ||
| + | |||
| + | ปัญหา Bipartite Matching | ||
| + | |||
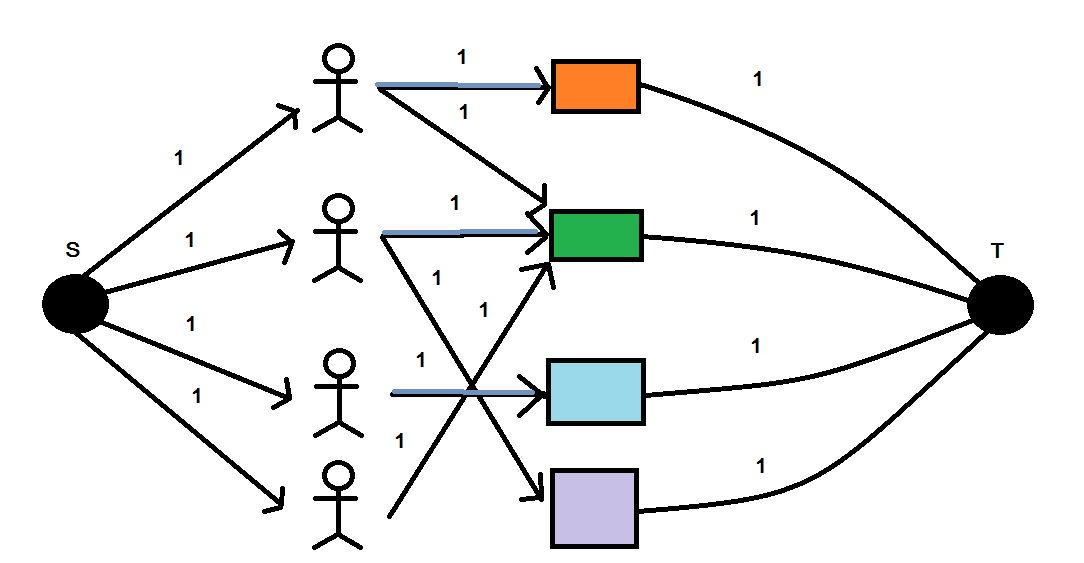
| + | [[ไฟล์:St_11.png]] | ||
| + | |||
| + | สมมุติว่า มีคน n คน ซื้อกับข้าว n ห่อ เส้นเชื่อมที่โยงไปคือ ที่สามารถกินข้าวห่อได้ ทำอย่างไรให้ทุกคนได้กินข้าวห่อ | ||
| + | |||
| + | สร้าง Supernode S กับSupernode T ใส่ทิศทางและ Capasity | ||
| + | |||
| + | หาคำตอบในกราฟนี้โดยใช้ maxflow จะ work ได้ maxflow ต้องเป็นจำนวนเต็ม | ||
รุ่นแก้ไขปัจจุบันเมื่อ 07:00, 24 กันยายน 2553
บันทึกคำบรรยายวิชา 204512-53 นี้ เป็นบันทึกที่นิสิตเขียนขึ้น เนื้อหาโดยมากยังไม่ผ่านการตรวจสอบอย่างละเอียด การนำไปใช้ควรระมัดระวัง
Algorithm Lecture #8 จดบันทึกคำบรรยายโดย:
นาย บดินทร์ แสงทองล้วน 5314550113
นาย วิชา มีสุขสบาย 5314550164
นาย อภิชาติ ทวีศิริเวทย์ 5314550199
เนื้อหา
Network flow problem
1. กราฟมีทิศทาง
2. ความจุ (capacity)
3. จุดเริ่มต้น source
4. จุดสิ้นสุด sink
5. flow เป็น function จาก
เงื่อนไข
1. Capacity constraints :
2. Skew symmetry :
3. conservation :
ปริมาตร flow
Maximum flow problem
Maximum flow problem: ปัญหาการหาปริมาณการไหลสูงสุด ซึ่งเป็นหนึ่งในปัญหาเน็ตเวิร์คโฟล์วที่น่าสนใจ
สัญลักษณ์ที่เกี่ยวข้อง
G คือ กราฟที่เราสนใจ
G = (V,E) คือ ฟังก์ชั่นของกราฟ G โดยที่ V คือ เซตของโหนด และ E คือเซตของเส้นเชื่อม
C: E->R+ คือ Capacity ของเส้นเชื่อม เซตจำนวนจริงบวกไม่รวมศูนย์ (0, +∞)
s-t คือ เซตของเส้นทางจาก s ไปถึง t
Maximum flow คือโจทย์หนึ่งของเน็ตเวิร์คโฟล์วโจทย์นี้ต้องการหาค่ามากที่สุดของโฟล์ว จากต้นทาง(s) ที่ส่งได้ไม่เกินความจุของเส้นเชื่อม(u) แต่ละเส้น เพื่อให้ได้ค่ารวมมากที่สุดจากต้นจนถึงปลายทาง (t)
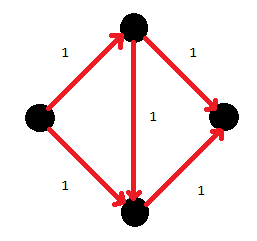
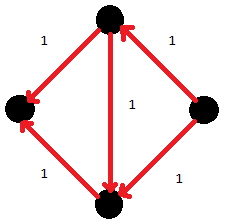
Classic problem
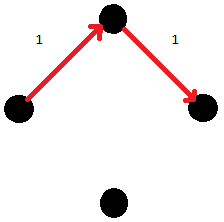
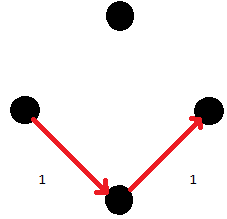
Maximum flow คือเท่าไหร่ : ต้องหา path มาเรื่อยๆ จนไม่มี path
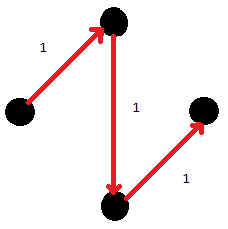
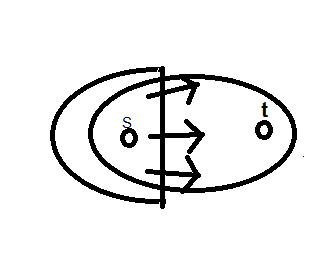
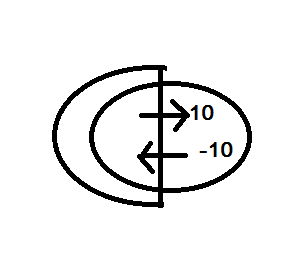
ถ้าได้รูปแบบข้างต้นก็ไม่มีปัญหา แต่ถ้าเกิดได้แบบ
จะกลายเป็นปัญหา แล้วจะแก้ไขอย่างไร?
แนวคิด
Algorithm
- F <- 0
- G(f) เป็น residual graph ของ f
- ถ้ามี path จาก s ไป t ใน G(f)
- P <- path จาก s ไป t ใน G(f)
- C <- capacity ต่ำสุดของเส้นเชื่อมใน path P
- Update f ด้วย flow path P ด้วยปริมาตร C
- หา G(f) <- residual graph ของ flow f
st-cut
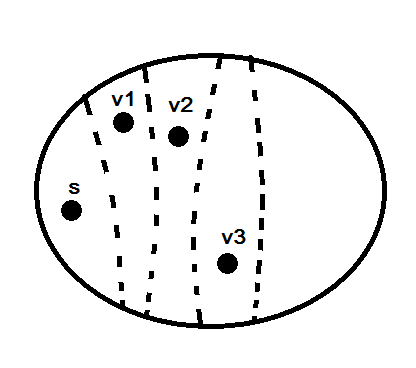
พิจารณา sub set ของ node กลุ่มหนึ่ง
ถ้า จะเรียก ว่า st-cut ;
cut ที่ตัด s กับ t ออกจากกัน
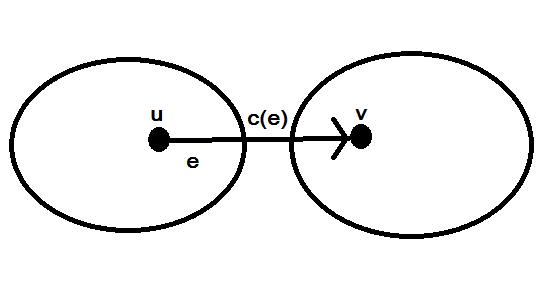
เราสนใจ edge ทั้งหมดที่ข้ามจาก s ไป t
1) นิยาม
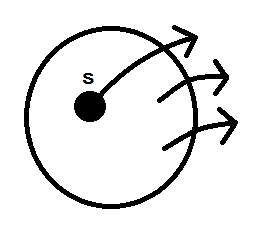
Flow ใดๆเราพิจารณาการส่ง volumeจาก s ไป t
ถ้าเราพิจารณา volume ที่วิ่งผ่าน cut ต้องเท่ากับ volume ที่ออกจาก S
2) นิยาม
; flow ที่วิ่งจาก ทั้งหมดเลย
flow สามารถวิ่งไปและวิ่่งกลับได้
สำหรับ st-cut ใดๆ เราได้ว่า
เราจะพิสูจน์
คือ Volume ของ f
พิสูจน์
สำหรับ st-cut S ใดๆ
พิสูจน์
สำหรับทุกๆ
พิสูจน์ โดย Induction ตั้งแต่ 0 ถึง k
เป็น base case ซึ่งจะเท่ากันตามนิยาม
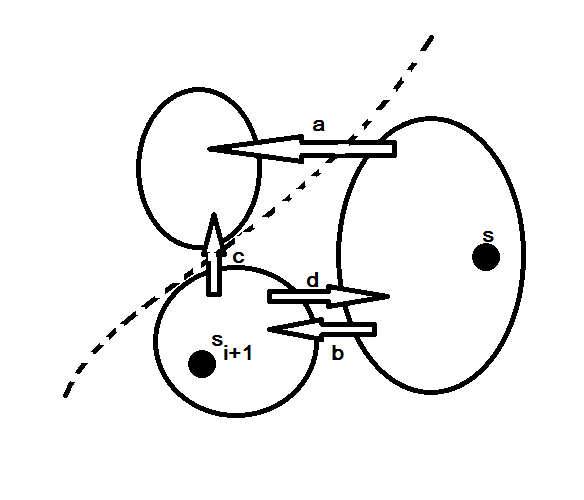
เราจะพิสูจน์ว่า
ได้ มี flow ที่วิ่งเข้าวิ่งออกของ c กับ d สุดท้ายรวม flow เส้นปะเข้า
ไปเราได้ว่า
เนื่องจากเรารู้ว่า
Claim(1)
Claim(2)
Ford-Fullerson
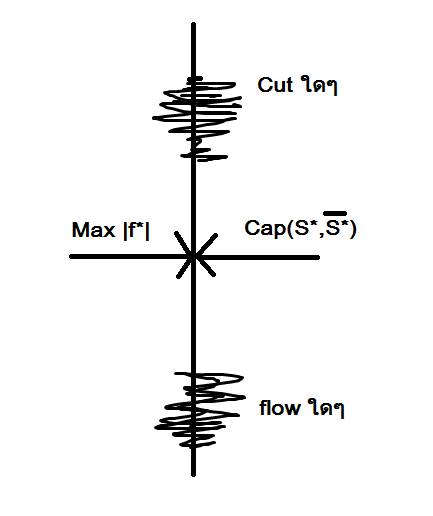
สำหรับ st-cut ใดๆ
เราพิจารณา flow มีขนาดเท่ากับ cut ใดๆ แปลว่า flow นั้นมีขนาดใหญ่สุด
เราสามารถพิสูจน์ต่อได้ว่า flow ที่มีขนาดเท่ากับ เราจะได้ flow ที่มีขนาดใหญ่ที่สุด
พิสูจน์ว่า
flow f ที่ out-put โดย Ford-Fullerson เป็น maximum flow
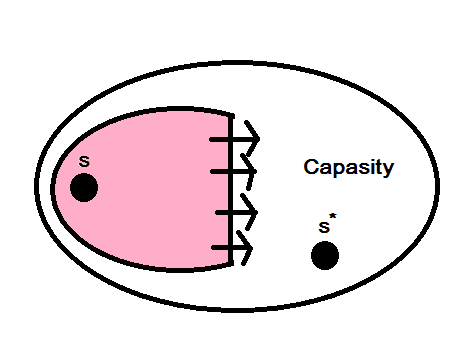
หา s-t cut ที่
เราต้องการ
พิสูจน์
1) flowต้องเต็ม
2) edgeที่วิ่งกลับต้องไม่มีflowเลย
เราพิสูจน์โดย By Contradition
พิจารณา e=(u,v) ที่
Claim
ถ้าไม่เท่ากัน flow จะไม่เต็ม เท่ากับว่ามี path อีก 1 path ใน residual graph เพราะฉะนั้น เป็นจริง
สิ่งที่เราได้นอกจากจะได้ max flow เราจะได้ min cut เพราะ max flow = min cap
เวลาในการทำงาน
ความคืบหน้าของมันคือจำนวน |f| เพิ่มขึ้นเรื่อยๆ แต่ต้องมันใจว่าไปถึง max flow ไม่ใช่เพิ่มขึ้นน้อยลงเรื่อยก็ไม่มีทางไปถึง
m คือจำนวน edge, n คือ จำนวน node; ทำทั่วไป ; หา path ;
ถ้า Capacity เป็น integer จำนวนรอบที่ใช้จะเท่ากับจำนวนของ max flow
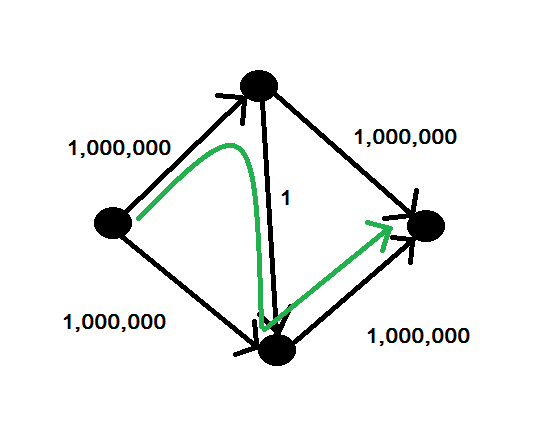
ตัวอย่างที่ Fold-Fullerson ล้มเหลว
Bipatite Matching
ปัญหาที่สามารถมองเป็น max flow ได้
กราฟ G จะเรียกว่าเป็น Bipatite graph ถ้า set ของ vertex V สามารถแบ่งเป็น
A,B ที่
แล้วไม่มีเส้นเชื่อม (u,v) ที่ หรือ
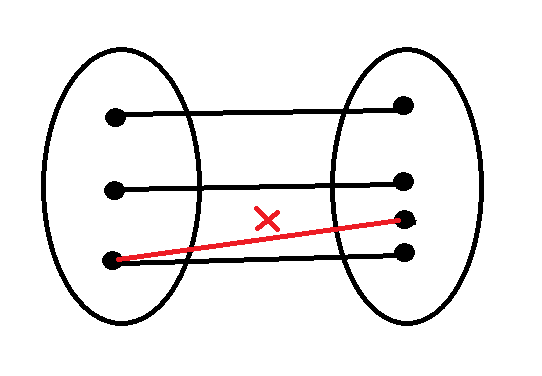
เซต เรียกว่าเป็น matching ถ้าไม่มีโหนดใดๆ ติดกับเส้นเชื่อม M เกิน 1 เส้น
ปัญหา Bipartite Matching
สมมุติว่า มีคน n คน ซื้อกับข้าว n ห่อ เส้นเชื่อมที่โยงไปคือ ที่สามารถกินข้าวห่อได้ ทำอย่างไรให้ทุกคนได้กินข้าวห่อ
สร้าง Supernode S กับSupernode T ใส่ทิศทางและ Capasity
หาคำตอบในกราฟนี้โดยใช้ maxflow จะ work ได้ maxflow ต้องเป็นจำนวนเต็ม