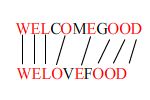ผลต่างระหว่างรุ่นของ "204512-53/lecture10"
Meta (คุย | มีส่วนร่วม) (หน้าที่ถูกสร้างด้วย '== Dynamic Programming == === ปัญหาที่ 1 เกมเก็บคะแนน === ไฟล์:ex1.jpg จากร…') |
|||
| (ไม่แสดง 48 รุ่นระหว่างกลางโดยผู้ใช้ 2 คน) | |||
| แถว 1: | แถว 1: | ||
| − | + | จดบันทึกคำบรรยายโดย: <br> | |
| + | นายธนพล พุฒธรรม 5214550103 <br> | ||
| + | นายประธาน สมบูรณ์ 5214550189 <br> | ||
| + | นายพีรพล บุญธกานนท์ 5214550197 <br> | ||
| + | นายเมธา จึงประเสริฐ 5214550227 <br> | ||
| − | === ปัญหาที่ 1 เกมเก็บคะแนน | + | == '''Dynamic Programming''' == |
| + | |||
| + | == '''ปัญหาที่ 1 เกมเก็บคะแนน''' == | ||
[[ไฟล์:ex1.jpg]] | [[ไฟล์:ex1.jpg]] | ||
| − | + | '''''จากรูป แต่ละ node มีคะแนนอยู่ ต้องเริ่มจาก start ไปยัง end จะวิ่งทางไหนให้ได้คะแนนรวมสูงสุด ?'''''<br> | |
| − | + | วิธีการพื้นฐานในการหาคำตอบ คือ ลองทุกทาง แล้วหาเส้นทางที่ได้ผลรวมคะแนนมากที่สุด จากความสูง k จะใช้เวลา O(2<sup>k</sup>) ซึ่งใช้เวลาในการหาคำตอบที่นานมาก<br> | |
พิจารณาปัญหาแบบ bottom-up ดูจากโหนดที่ 1 -> 2 -> … -> n ที่โหนด 2 และ โหนด 3 การจะไปที่โหนด 5 จะเกิดการทับซ้อนของปัญหา จะต้องการเลือกเส้นทางที่มีคะแนนมากกว่า<br> | พิจารณาปัญหาแบบ bottom-up ดูจากโหนดที่ 1 -> 2 -> … -> n ที่โหนด 2 และ โหนด 3 การจะไปที่โหนด 5 จะเกิดการทับซ้อนของปัญหา จะต้องการเลือกเส้นทางที่มีคะแนนมากกว่า<br> | ||
| แถว 12: | แถว 18: | ||
พิจารณาปัญหาแบบ top-down ดูจากโหนดที่ n -> (n-1) -> … -> 1 สังเกตโหนดที่ 5 จะเกิดการทับซ้อนของปัญหา จะต้องการเลือกเส้นทางที่มีคะแนนมากกว่าจาก 2 เส้นทางคือโหนด 2 หรือโหนด 3<br> | พิจารณาปัญหาแบบ top-down ดูจากโหนดที่ n -> (n-1) -> … -> 1 สังเกตโหนดที่ 5 จะเกิดการทับซ้อนของปัญหา จะต้องการเลือกเส้นทางที่มีคะแนนมากกว่าจาก 2 เส้นทางคือโหนด 2 หรือโหนด 3<br> | ||
| − | + | == '''ปัญหาที่ 2 วิธีการเดินทาง''' == | |
| − | |||
[[ไฟล์:ex2.jpg]] | [[ไฟล์:ex2.jpg]] | ||
| − | วิธีเดินทางจากโหนด A ไปยังโหนด B ไปได้กี่วิธี<br> | + | '''''วิธีเดินทางจากโหนด A ไปยังโหนด B ไปได้กี่วิธี ?'''''<br> |
วิธีที่ง่ายสุดนับทุกเส้นทางจากโหนด A ไปยังโหนด B จากรูปมีเส้นเชื่อมโหนดครบทุกเส้นทำให้สามารถคำนวณได้เลยไม่ต้องนับ จะได้ <math>\binom{8}{5}</math> หรือ <math>\binom{8}{3}</math> จะได้ 56 วิธี <br> | วิธีที่ง่ายสุดนับทุกเส้นทางจากโหนด A ไปยังโหนด B จากรูปมีเส้นเชื่อมโหนดครบทุกเส้นทำให้สามารถคำนวณได้เลยไม่ต้องนับ จะได้ <math>\binom{8}{5}</math> หรือ <math>\binom{8}{3}</math> จะได้ 56 วิธี <br> | ||
| แถว 23: | แถว 28: | ||
[[ไฟล์:ex2_1.jpg]] | [[ไฟล์:ex2_1.jpg]] | ||
| − | + | จากรูป ด้านบนถ้าเส้นเชื่อมไม่ครบทุกโหนดการคำนวณทำได้ยาก การจะนับทีละเส้นทางจาก A -> B ใช้เวลานาน ถ้าพิจารณาจากโหนด B ย้อนกลับขึ้นไป การจะรู้ค่าที่โหนด B ต้องรู้ค่าของ 2 โหนดก่อนหน้า โหนดก่อนหน้าก็ต้องรู้ค่าของ 2 โหนดก่อนหน้าถัดไปอีกเรื่อยๆ จนถึงโหนด A ดังนั้นถ้ามีการบันทึกค่าที่โหนดปัจจุบันไว้จะทำให้โหนดถัดมาใช้ค่าได้เลยไม่ต้องเริ่มใหม่ทำให้หาวิธีเดินทางได้ 20 วิธีดังนี้ <br> | |
[[ไฟล์:ex2_2.jpg]] | [[ไฟล์:ex2_2.jpg]] | ||
| − | == ปัญหาที่ 3 ปัญหาการขึ้นบันได == | + | == '''ปัญหาที่ 3 ปัญหาการขึ้นบันได''' == |
| + | |||
| + | '''''มีบันได n ขั้น มีวิธีการเดินขึ้นบันไดได้กี่แบบ ?''''' | ||
| + | |||
| + | 1) พิจารณาจากข้างบนลงมาข้างล่าง (Top down) จะมองได้ง่ายกว่า โดยจากขั้นที่ n จำนวนรูปแบบการขึ้นบันไดมาขั้นที่ n ต้องรู้รูปแบบการขึ้น 2 ขั้นก่อนหน้า (ขั้นที่ n-1 และ n-2) ถ้าให้ F(n) แทนจำนวนรูปแบบการขึ้นบันไดขั้นที่ n จะได้ว่า | ||
| + | |||
| + | ''' F(n) = F(n-1) + F(n-2)''' | ||
| + | |||
| + | การหาด้วยวิธีการนี้จะรันช้ามากเพราะ F(n) โตแบบ Exponential เช่น อยากรู้ F(7) ต้องหา F(6) และ F(5) | ||
| + | |||
| + | [[ไฟล์:ex3_1.jpg]] [[ไฟล์:ex3_2.jpg]] | ||
| + | |||
| + | 2) พิจารณาจากข้างล่างขึ้นบน (Buttom up) | ||
| + | ที่ 0 ขั้น เดินได้กี่แบบ | ||
| + | ที่ 1 ขั้น เดินได้กี่แบบ | ||
| + | . | ||
| + | . | ||
| + | . | ||
| + | ที่ n ขั้น เดินได้กี่แบบ | ||
| − | + | [[ไฟล์:ex3_4.jpg]] | |
| − | + | การหาด้วยวิธีการนี้จะรันได้เร็วมาก เพราะการหาค่า F(7) ก็นำเอา F(6) + F(5) = F(7) ดังนั้น การหา F(n) จะใช้เวลา O(n) ซึ่งลำดับแบบนี้จะเรียกว่า "ลำดับฟีโบนักชี" | |
| − | == ปัญหาที่ 4 การแบ่งหุ้น == | + | == '''ปัญหาที่ 4 การแบ่งหุ้น''' == |
| − | มีใบหุ้น nใบ แต่ละใบมีมูลค่า a<sub>1</sub>, a<sub>2</sub>, a<sub>3</sub>, …, a<sub>n</sub> | + | '''''มีใบหุ้น nใบ แต่ละใบมีมูลค่า a<sub>1</sub>, a<sub>2</sub>, a<sub>3</sub>, …, a<sub>n</sub> จะจัดแบ่งได้กี่รูปแบบ ?'''''<br> |
| − | ถ้ามีใบหุ้น 10 ใบมูลค่าดังนี้ 1, 4, 2, 1, 3, 4, 7, 10, 16 จัดรูปแบบได้ดังนี้<br> | + | เช่น ถ้ามีใบหุ้น 10 ใบมูลค่าดังนี้ 1, 4, 2, 1, 3, 4, 7, 10, 16 จัดรูปแบบได้ดังนี้<br> |
{|border=1 | {|border=1 | ||
! || 0 || 1 || 2 || 3 || 4 || 5 || 6 || 7 || 8 || 9 || 10 || 11 || 12 || 13 || 14 || 15 || 16 || 17 || 18 || 19 || 20 || 21 || 22 || 23 || 24 || 25 || 26 || 27 || 28 || 29 || 30 || 31 || 32 || 33 || 34 || 35 || 36 || 37 || 38 || 39 || 40 || 41 || 42 || 43 || 44 || 45 || 46 || 47 | ! || 0 || 1 || 2 || 3 || 4 || 5 || 6 || 7 || 8 || 9 || 10 || 11 || 12 || 13 || 14 || 15 || 16 || 17 || 18 || 19 || 20 || 21 || 22 || 23 || 24 || 25 || 26 || 27 || 28 || 29 || 30 || 31 || 32 || 33 || 34 || 35 || 36 || 37 || 38 || 39 || 40 || 41 || 42 || 43 || 44 || 45 || 46 || 47 | ||
| แถว 60: | แถว 83: | ||
| 16 || x || x || x || x||x || x||x ||x ||x ||x ||x ||x || x||x ||x ||x ||x ||x ||x ||x ||x ||x || x||x ||x ||x || x||x ||x ||x || x||x || x||x ||x ||x ||x ||x ||x ||x ||x ||x || x||x ||x ||x ||x ||x | | 16 || x || x || x || x||x || x||x ||x ||x ||x ||x ||x || x||x ||x ||x ||x ||x ||x ||x ||x ||x || x||x ||x ||x || x||x ||x ||x || x||x || x||x ||x ||x ||x ||x ||x ||x ||x ||x || x||x ||x ||x ||x ||x | ||
|} | |} | ||
| + | |||
| + | ถ้ามี a<sub>1</sub>, a<sub>2</sub>, a<sub>3</sub>, …, a<sub>i</sub> จะมีวิธีรวมให้ได้มูลค่า x บาทหรือไม่ | ||
| + | ให้ B(i,x) แทนจำนวนเงินที่ i รวมได้ x บาท<br> | ||
| + | ถ้าใช้ใบหุ้นที่ a<sub>i</sub> จะได้ B(i-1,x)<br> | ||
| + | ถ้าไม่ใช้ใบหุ้นที่ a<sub>i</sub> จะได้ B(i-1,x- a<sub>i</sub>)<br> | ||
| + | B(i,x) = B(i-1,x) V B(i-1,x- a<sub>i</sub>) | ||
| + | |||
| + | == '''ปัญหาที่ 5 การตั้งร้านกาแฟ ''' == | ||
| + | |||
| + | ต้องการตั้งร้านขายกาแฟริมถนนให้ได้มูลค่ารวมสูงสุด โดยไม่สามารถตั้งร้านได้ติดกัน 2 ตำแหน่ง <br> | ||
| + | |||
| + | [[ไฟล์:ex5.jpg]] | ||
| + | |||
| + | ถ้าสถานที่ตั้งร้านมีมูลค่า b<sub>1</sub>, b<sub>2</sub>, b<sub>3</sub>, …, b<sub>i</sub> ตั้งร้านกาแฟได้ตามเงื่อนไขสูงสุดเท่าไร<br> | ||
| + | ให้ V(i) แทนมูลค่าสูงสุดที่ตั้งร้านตำแหน่งที่ i | ||
| + | |||
| + | V(i) = max | ||
| + | <math>\begin{cases} | ||
| + | bi+V(i-3) \\ | ||
| + | V(i-1) | ||
| + | \end{cases}</math><br> | ||
| + | ถ้ามีมูลค่าร้านแต่ละตำแหน่งคือ 10, 10000, 10, 10, 100, 10000, 10, 10, 5000, 7000, 2000, 5000, 10 นำมาเขียนตารางได้ดังนี้<br> | ||
| + | |||
| + | {|border=1 | ||
| + | ! i||-2 || -1 || 0 || 1 || 2 || 3 || 4 || 5 || 6 || 7 || 8 || 9 || 10 || 11 || 12 || 13 | ||
| + | |- | ||
| + | | b||0 || 0 || 0 || 10 || 10000|| 10|| 10|| 100|| 10000|| 10|| 10|| 5000|| 7000|| 2000|| 5000|| 10 | ||
| + | |- | ||
| + | | || || || || 0|| 10000|| 10|| 20|| 10100|| 20000|| 10010|| 10110|| 25000|| 27000|| 22000|| 30000|| 27000 | ||
| + | |- | ||
| + | | || || || || 10 || 10 || 10000 || 10000 || 10000 || 10100 || 20000 || 20000 || 20000 || 25000 || 27000|| 27000 || 30000 | ||
| + | |- | ||
| + | | V||0 || 0 || 0 || 10|| 10000|| 10000|| 10000|| 10100|| 20000|| 20000|| 20000|| 25000|| 27000|| 27000|| 30000|| 30000 | ||
| + | |} | ||
| + | <br> | ||
| + | จะได้มูลค่าตั้งร้านรวมสูงสุดคือ 30000 และถ้าต้องการทราบว่าตำแหน่งไหนบ้างที่ต้องเปิดร้านก็เพิ่มการเก็บตำแหน่งไว้ | ||
| + | |||
| + | == '''ปัญหาที่ 6 ลำดับย่อยเพิ่มขึ้นที่ยาวที่สุด (Longest Increasing Subsequence)''' == | ||
| + | |||
| + | มีลำดับ a<sub>1</sub>, a<sub>2</sub>, a<sub>3</sub>, …, a<sub>i</sub> ต้องการหาลำดับย่อยที่เพิ่มขึ้นที่ยาวที่สุดที่สิ้นสุดที่ a<sub>i</sub> ยาวเท่าไร<br> | ||
| + | ตัวอย่าง 1,2,2,3,4 ลำดับย่อยเพิ่มขึ้นที่ยาวที่สุดคือ 1,2,3,4 ความยาว 4 <br> | ||
| + | ให้ L(i) แทนความยาวของลำดับเพิ่มขึ้นที่สิ้นสุดที่ a<sub>i</sub> <br> | ||
| + | จะได้ว่า L(i) = 1 + max(L(j)) เมื่อ j<i และ a<sub>j</sub><a<sub>i</sub><br> | ||
| + | |||
| + | == '''ปัญหาที่ 7 ลำดับย่อยร่วมที่ยาวที่สุด (Longest Common Subsequence)''' == | ||
| + | |||
| + | มี string 2 string ต้องการหา substring ที่ร่วมที่ยาวที่สุด เช่น | ||
| + | S = WELCOMEGOOD | ||
| + | T = WELOVEFOOD | ||
| + | |||
| + | [[ไฟล์:ex6.jpg]] | ||
| + | |||
| + | จะมี substring ที่ยาวที่สุดคือ WELOEOOD ความยาว 8<br> | ||
| + | ให้ A(i,j) เป็นความยาว substring ร่วมที่ยาวที่สุดตำแหน่ง S<sub>i</sub> และ T<sub>j</sub><br> | ||
| + | สร้าง recurrence ดังนี้ <br> | ||
| + | A(i,j) = max | ||
| + | <math>\begin{cases} | ||
| + | 1+A(i-1,j-1) ; S[i] = T[j] \\ | ||
| + | A(i-1,j) ; S[i] = T[j-1]\\ | ||
| + | A(i,j-1) ; S[i-1] = T[j] | ||
| + | \end{cases}</math> | ||
รุ่นแก้ไขปัจจุบันเมื่อ 16:33, 11 ตุลาคม 2553
จดบันทึกคำบรรยายโดย:
นายธนพล พุฒธรรม 5214550103
นายประธาน สมบูรณ์ 5214550189
นายพีรพล บุญธกานนท์ 5214550197
นายเมธา จึงประเสริฐ 5214550227
เนื้อหา
- 1 Dynamic Programming
- 2 ปัญหาที่ 1 เกมเก็บคะแนน
- 3 ปัญหาที่ 2 วิธีการเดินทาง
- 4 ปัญหาที่ 3 ปัญหาการขึ้นบันได
- 5 ปัญหาที่ 4 การแบ่งหุ้น
- 6 ปัญหาที่ 5 การตั้งร้านกาแฟ
- 7 ปัญหาที่ 6 ลำดับย่อยเพิ่มขึ้นที่ยาวที่สุด (Longest Increasing Subsequence)
- 8 ปัญหาที่ 7 ลำดับย่อยร่วมที่ยาวที่สุด (Longest Common Subsequence)
Dynamic Programming
ปัญหาที่ 1 เกมเก็บคะแนน
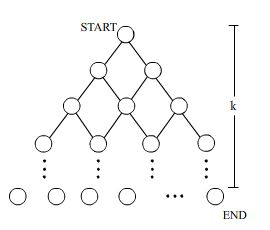
จากรูป แต่ละ node มีคะแนนอยู่ ต้องเริ่มจาก start ไปยัง end จะวิ่งทางไหนให้ได้คะแนนรวมสูงสุด ?
วิธีการพื้นฐานในการหาคำตอบ คือ ลองทุกทาง แล้วหาเส้นทางที่ได้ผลรวมคะแนนมากที่สุด จากความสูง k จะใช้เวลา O(2k) ซึ่งใช้เวลาในการหาคำตอบที่นานมาก
พิจารณาปัญหาแบบ bottom-up ดูจากโหนดที่ 1 -> 2 -> … -> n ที่โหนด 2 และ โหนด 3 การจะไปที่โหนด 5 จะเกิดการทับซ้อนของปัญหา จะต้องการเลือกเส้นทางที่มีคะแนนมากกว่า
พิจารณาปัญหาแบบ top-down ดูจากโหนดที่ n -> (n-1) -> … -> 1 สังเกตโหนดที่ 5 จะเกิดการทับซ้อนของปัญหา จะต้องการเลือกเส้นทางที่มีคะแนนมากกว่าจาก 2 เส้นทางคือโหนด 2 หรือโหนด 3
ปัญหาที่ 2 วิธีการเดินทาง
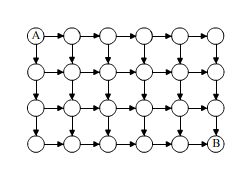
วิธีเดินทางจากโหนด A ไปยังโหนด B ไปได้กี่วิธี ?
วิธีที่ง่ายสุดนับทุกเส้นทางจากโหนด A ไปยังโหนด B จากรูปมีเส้นเชื่อมโหนดครบทุกเส้นทำให้สามารถคำนวณได้เลยไม่ต้องนับ จะได้ หรือ จะได้ 56 วิธี
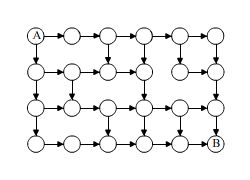
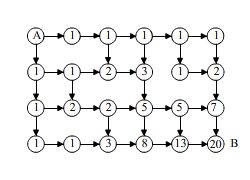
จากรูป ด้านบนถ้าเส้นเชื่อมไม่ครบทุกโหนดการคำนวณทำได้ยาก การจะนับทีละเส้นทางจาก A -> B ใช้เวลานาน ถ้าพิจารณาจากโหนด B ย้อนกลับขึ้นไป การจะรู้ค่าที่โหนด B ต้องรู้ค่าของ 2 โหนดก่อนหน้า โหนดก่อนหน้าก็ต้องรู้ค่าของ 2 โหนดก่อนหน้าถัดไปอีกเรื่อยๆ จนถึงโหนด A ดังนั้นถ้ามีการบันทึกค่าที่โหนดปัจจุบันไว้จะทำให้โหนดถัดมาใช้ค่าได้เลยไม่ต้องเริ่มใหม่ทำให้หาวิธีเดินทางได้ 20 วิธีดังนี้
ปัญหาที่ 3 ปัญหาการขึ้นบันได
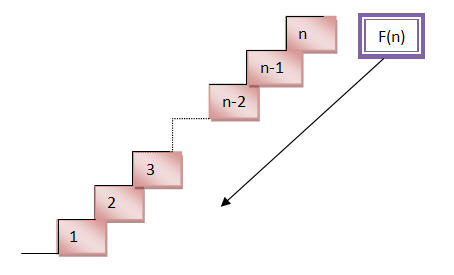
มีบันได n ขั้น มีวิธีการเดินขึ้นบันไดได้กี่แบบ ?
1) พิจารณาจากข้างบนลงมาข้างล่าง (Top down) จะมองได้ง่ายกว่า โดยจากขั้นที่ n จำนวนรูปแบบการขึ้นบันไดมาขั้นที่ n ต้องรู้รูปแบบการขึ้น 2 ขั้นก่อนหน้า (ขั้นที่ n-1 และ n-2) ถ้าให้ F(n) แทนจำนวนรูปแบบการขึ้นบันไดขั้นที่ n จะได้ว่า
F(n) = F(n-1) + F(n-2)
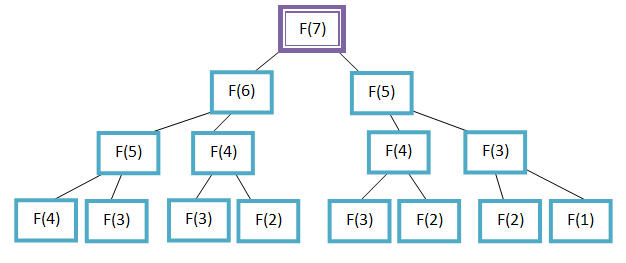
การหาด้วยวิธีการนี้จะรันช้ามากเพราะ F(n) โตแบบ Exponential เช่น อยากรู้ F(7) ต้องหา F(6) และ F(5)
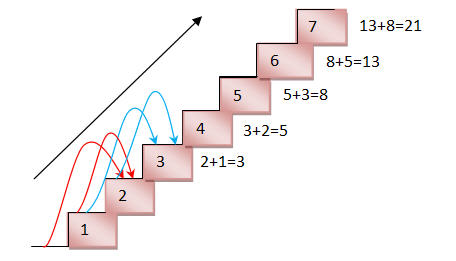
2) พิจารณาจากข้างล่างขึ้นบน (Buttom up)
ที่ 0 ขั้น เดินได้กี่แบบ ที่ 1 ขั้น เดินได้กี่แบบ . . . ที่ n ขั้น เดินได้กี่แบบ
การหาด้วยวิธีการนี้จะรันได้เร็วมาก เพราะการหาค่า F(7) ก็นำเอา F(6) + F(5) = F(7) ดังนั้น การหา F(n) จะใช้เวลา O(n) ซึ่งลำดับแบบนี้จะเรียกว่า "ลำดับฟีโบนักชี"
ปัญหาที่ 4 การแบ่งหุ้น
มีใบหุ้น nใบ แต่ละใบมีมูลค่า a1, a2, a3, …, an จะจัดแบ่งได้กี่รูปแบบ ?
เช่น ถ้ามีใบหุ้น 10 ใบมูลค่าดังนี้ 1, 4, 2, 1, 3, 4, 7, 10, 16 จัดรูปแบบได้ดังนี้
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | x | |||||||||||||||||||||||||||||||||||||||||||||||
| 1 | x | x | ||||||||||||||||||||||||||||||||||||||||||||||
| 4 | x | x | x | x | ||||||||||||||||||||||||||||||||||||||||||||
| 2 | x | x | x | x | x | x | x | |||||||||||||||||||||||||||||||||||||||||
| 1 | x | x | x | x | x | x | x | x | ||||||||||||||||||||||||||||||||||||||||
| 3 | x | x | x | x | x | x | x | x | x | x | x | |||||||||||||||||||||||||||||||||||||
| 4 | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x | |||||||||||||||||||||||||||||||||
| 7 | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x | ||||||||||||||||||||||||||
| 10 | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x | ||||||||||||||||
| 16 | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x |
ถ้ามี a1, a2, a3, …, ai จะมีวิธีรวมให้ได้มูลค่า x บาทหรือไม่
ให้ B(i,x) แทนจำนวนเงินที่ i รวมได้ x บาท
ถ้าใช้ใบหุ้นที่ ai จะได้ B(i-1,x)
ถ้าไม่ใช้ใบหุ้นที่ ai จะได้ B(i-1,x- ai)
B(i,x) = B(i-1,x) V B(i-1,x- ai)
ปัญหาที่ 5 การตั้งร้านกาแฟ
ต้องการตั้งร้านขายกาแฟริมถนนให้ได้มูลค่ารวมสูงสุด โดยไม่สามารถตั้งร้านได้ติดกัน 2 ตำแหน่ง
ถ้าสถานที่ตั้งร้านมีมูลค่า b1, b2, b3, …, bi ตั้งร้านกาแฟได้ตามเงื่อนไขสูงสุดเท่าไร
ให้ V(i) แทนมูลค่าสูงสุดที่ตั้งร้านตำแหน่งที่ i
V(i) = max
ถ้ามีมูลค่าร้านแต่ละตำแหน่งคือ 10, 10000, 10, 10, 100, 10000, 10, 10, 5000, 7000, 2000, 5000, 10 นำมาเขียนตารางได้ดังนี้
| i | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| b | 0 | 0 | 0 | 10 | 10000 | 10 | 10 | 100 | 10000 | 10 | 10 | 5000 | 7000 | 2000 | 5000 | 10 |
| 0 | 10000 | 10 | 20 | 10100 | 20000 | 10010 | 10110 | 25000 | 27000 | 22000 | 30000 | 27000 | ||||
| 10 | 10 | 10000 | 10000 | 10000 | 10100 | 20000 | 20000 | 20000 | 25000 | 27000 | 27000 | 30000 | ||||
| V | 0 | 0 | 0 | 10 | 10000 | 10000 | 10000 | 10100 | 20000 | 20000 | 20000 | 25000 | 27000 | 27000 | 30000 | 30000 |
จะได้มูลค่าตั้งร้านรวมสูงสุดคือ 30000 และถ้าต้องการทราบว่าตำแหน่งไหนบ้างที่ต้องเปิดร้านก็เพิ่มการเก็บตำแหน่งไว้
ปัญหาที่ 6 ลำดับย่อยเพิ่มขึ้นที่ยาวที่สุด (Longest Increasing Subsequence)
มีลำดับ a1, a2, a3, …, ai ต้องการหาลำดับย่อยที่เพิ่มขึ้นที่ยาวที่สุดที่สิ้นสุดที่ ai ยาวเท่าไร
ตัวอย่าง 1,2,2,3,4 ลำดับย่อยเพิ่มขึ้นที่ยาวที่สุดคือ 1,2,3,4 ความยาว 4
ให้ L(i) แทนความยาวของลำดับเพิ่มขึ้นที่สิ้นสุดที่ ai
จะได้ว่า L(i) = 1 + max(L(j)) เมื่อ j<i และ aj<ai
ปัญหาที่ 7 ลำดับย่อยร่วมที่ยาวที่สุด (Longest Common Subsequence)
มี string 2 string ต้องการหา substring ที่ร่วมที่ยาวที่สุด เช่น S = WELCOMEGOOD T = WELOVEFOOD
จะมี substring ที่ยาวที่สุดคือ WELOEOOD ความยาว 8
ให้ A(i,j) เป็นความยาว substring ร่วมที่ยาวที่สุดตำแหน่ง Si และ Tj
สร้าง recurrence ดังนี้
A(i,j) = max