ผลต่างระหว่างรุ่นของ "204512/บรรยาย 13"
| (ไม่แสดง 187 รุ่นระหว่างกลางโดยผู้ใช้ 10 คน) | |||
| แถว 5: | แถว 5: | ||
<br /> | <br /> | ||
---- | ---- | ||
| − | == NP Completeness== | + | == NP Completeness == |
| + | '''NP : Non-deterministic Polynomial time''' ปัญหาที่เป็น NP เป็นปัญหาที่ไม่สามารถแก้ได้ภายใน polynomial time เป็นวิธีหนึ่งที่จะแสดงว่าปัญหาที่กล่าวถึงนั้นยาก แต่ก่อนที่จะกล่าวถึงปัญหาที่อยู่ใน NP Class จะกล่าวถึงปัญหาที่ไม่มีอัลกอริทึมใดแก้ได้ก่อนนั่นคือ ปัญหา Halting problem | ||
| + | '''Note : '''ปัญหา Halting problem ไม่ใช่ปัญหาใน NP Class เพราะไม่สามารถแก้ได้ | ||
=== ปัญหา Halting Problem === | === ปัญหา Halting Problem === | ||
| แถว 13: | แถว 15: | ||
'''Proof :''' สมมติให้มีอัลกอริทึม Q ที่แก้ปัญหา Halting Problem ได้ | '''Proof :''' สมมติให้มีอัลกอริทึม Q ที่แก้ปัญหา Halting Problem ได้ | ||
โดยมี Q(program P, input X) จะ return True ถ้า P(x) halt และ return False เมื่อ P(x) ติด loop | โดยมี Q(program P, input X) จะ return True ถ้า P(x) halt และ return False เมื่อ P(x) ติด loop | ||
| − | เพราะฉะนั้นเราจะสามารถสร้าง procedure Q' | + | เพราะฉะนั้นเราจะสามารถสร้าง procedure Q' ที่มีอัลกอริทึมดังต่อไปนี้ได้ |
'''Procedure''' Q'(program P) | '''Procedure''' Q'(program P) | ||
| แถว 23: | แถว 25: | ||
จาก procedure Q' พิจารณา Q'(Q') ว่า halt หรือไม่ | จาก procedure Q' พิจารณา Q'(Q') ว่า halt หรือไม่ | ||
| − | Case1 : Q'(Q') halt | + | '''Case1 : Q'(Q') halt''' |
| − | นั่นคือ Q(Q',Q') = False --> Q'(Q') = False คือ Q'(Q') ติด loop *Contradict* | + | <br/>นั่นคือ Q(Q',Q') = False --> Q'(Q') = False คือ Q'(Q') ติด loop '''*Contradict''' |
| + | <br/>'''Case2 : Q'(Q') loop''' | ||
| + | <br/>นั่นคือ Q(Q',Q') = Ture --> Q'(Q') = True คือ Q'(Q') halt '''*Contradict''' | ||
| − | + | เกิด Contradiction จึงสรุปได้ว่าไม่สามารถสร้าง procedure Q' ได้ | |
| − | + | เพราะฉะนั้น สมมติฐานที่มีอัลกอริทึม Q ที่แก้ปัญหา Halting Problem ได้ ไม่เป็นจริง | |
| + | <br/><br/> | ||
| + | '''Note :''' ปัญหา Halting problem ถูกพิสูจน์โดย '''Alan Turing''' | ||
| − | + | === ปัญหา Program Equivalence === | |
| − | + | '''Description :''' ให้โปรแกรม P1 และ P2 ถามว่า P1 และ P2 ให้ผลลัพธ์เหมือนกันในทุกๆ input หรือไม่ | |
| + | ในที่นี้เราจะพิสูจน์โดยวิธี Reduction จากปัญหา Halting Problem (HP) ไปสู่ปัญหา Program Equivalence (PE) | ||
| + | |||
| + | '''Proof :''' สมมติว่ามีอัลกอริทึม Q ที่แก้ปัญหา Program Equivalence ได้ <br/> | ||
| + | ให้มี procedure HP(P,x) สำหรับแก้ปัญหา Halting Problem <br/> | ||
| + | - สร้าง program P' ที่ทำงานเหมือน P(x) แต่ไม่รับ input และไม่มี output แต่ก่อนจบพิมพ์ "done" <br/> | ||
| + | - สร้าง program P" ที่ไม่ทำอะไรพิมพ์ "done" อย่างเดียว <br/> | ||
| + | - ให้ procedure นี้ return Q(P',P") <br/> | ||
| + | เพราะเราสามารถบอกได้ว่า HP(P,x) ไม่สามารถแก้ได้ดังนั้น Q(P',P") ไม่สามารถแก้ได้ด้วยคือ reduction จาก HP ไป PE<br/><br/> | ||
| + | {{กล่องนิยาม| | ||
| + | ;Reduction:จะแสดงว่าปัญหา X ยาก ถ้าทราบว่าปัญหา Y ยาก จะสามารถบอกได้ว่าปัญหา X ยาก โดย ตั้งสมมติฐานว่าถ้าแก้ปัญหา X ได้จะแก้ปัญหา Y ได้ด้วย ถ้าสามารถพิสูจน์สมมติฐานนี้ว่าเป็นจริงได้ จะสามารถสรุปได้ว่า ปัญหา X แก้ไม่ได้ เพราะปัญหา Y แก้ไม่ได้ เป็นการพิสูจน์แบบ Reduction จาก Y ไป X}}<br/> | ||
| + | |||
| + | == Decision Problem == | ||
| + | '''Description :''' คือปัญหาที่ต้องการคำตอบเป็น Yes หรือ No<br/><br/> | ||
| + | ปัญหา Decision Problem P สามารถนิยามใหม่ ด้วย Language P ซึ่งเป็นเซ็ตของ instance ที่ตอบ yes เช่น<br/> | ||
| + | |||
| + | <u>'''Decision Problem'''</u> | ||
| − | + | '''Prime :''' ให้จำนวนจริง X ถามว่า X เป็น prime หรือไม่<br/> | |
| + | '''Shortest path :''' ให้หาว่ามี Shortest path จาก s ไป t ที่ยาวไม่เกิน p หรือไม่<br/> | ||
| − | + | <u>'''Language'''</u> | |
| − | + | '''Prime :''' {3, 5, 7, 11, ...} <br/> | |
| + | '''Shortest path :''' {...} (set ของ Shortest path จาก s ไป t ที่ยาวไม่เกิน p)<br/><br/> | ||
| + | {{กล่องนิยาม| | ||
| + | '''นิยาม :''' '''Problem''' คือกลุ่มของปัญหา '''Instance''' คือตัวปัญหาแต่ละตัว | ||
| + | }}<br/> | ||
| + | มีปัญหา A กับ B จะกล่าวว่า A สามารถลดรูป (reducible) ไปยัง B ได้แบบ polynomial time<br/> | ||
| + | ถ้ามี function T ทำงานใน polynomial time ที่ <br/> | ||
| + | ::: <math>\forall instance\ x \in A\ ,\ T(x) \in B</math><br/> | ||
| + | ::: และ <math>\forall instance\ x \notin A\ ,\ T(x) \notin B</math><br/> | ||
| + | ::: หรือเขียนอีกอย่างหนึ่งได้ว่า <math>\ x \in A\ \Leftrightarrow \ T(x) \in B</math><br/> | ||
| + | เขียนแทนด้วย <br/> | ||
| + | ::: <math>\mathit{A} \le \mathit{B}</math><br/> | ||
| + | ถ้าต้องการวัดประสิทธิภาพของ <math>A</math> ว่าทำงานเป็น polynomail time ไหม และทราบว่า B ทำงานใน polynomail time ให้หาว่ามี T ที่ทำงานใน polynomail time และเป็นไปตามข้อกำหนดด้านบนไหม แสดงว่า A ทำงานได้ใน polynomail time และเขียนแทนด้วย <math>\mathit{A} \le_p \mathit{B}</math><br/> | ||
=== ปัญหา Satisfiability (SAT) === | === ปัญหา Satisfiability (SAT) === | ||
| + | '''นิยาม : CNF formula''' คือนิพจน์ทางตรรกศาสตร์ที่เขียนให้อยู่ในรูปของการ AND กันของ Clause ที่เป็นการ OR กับของตัวแปรหรือนิเสธของตัวแปร <br/> | ||
| + | ตัวอย่างเช่น<br/> | ||
| + | <center><math>(X_1 \lor X_2) \land (X_3 \lor X_2 \lor \neg X_1) \land (\neg X_3 \lor \neg X_2 \lor X_1 \lor X_4)</math></center><br/> | ||
| + | ปัญหา SAT คือ กำหนด CNF formula <math>\boldsymbol{\phi}</math> ให้ถามว่า มีวิธีกำหนดค่าให้กับตัวแปรต่างๆ ใน <math>\boldsymbol{\phi}</math> ที่ทำให้ <math>\boldsymbol{\phi}</math> เป็นจริงหรือไม่<br/> | ||
| + | '''Note :''' Clause ที่เป็นการ OR กับของตัวแปรหรือนิเสธของตัวแปร เรียกว่า Disjunction ตัวอย่างเช่น <math>(X_1 \lor X_2)</math> | ||
=== ปัญหา 3-Satisfiability (3-SAT) === | === ปัญหา 3-Satisfiability (3-SAT) === | ||
| + | รับค่า CNF Formula <math>\boldsymbol{\phi}</math> ที่แต่ละ clause มีตัวแปร <math>\le</math> 3 ตัว | ||
| + | ถามว่าทำให้ <math>\boldsymbol{\phi}</math> เป็นจริงได้หรือไม่ ? | ||
| + | :::กรณี <math>3-SAT \le_p SAT</math> | ||
| + | ในกรณีนี้เป็นจริงอยู่แล้วเพราะ 3-SAT เป็นกรณีเฉพาะของ SAT แต่เราต้องการพิสูจน์ว่า | ||
| + | :::<math>SAT \le_p 3-SAT</math> | ||
| + | plan: แสดงว่าสำหรับ CNF <math>\boldsymbol{\phi}</math> ใดๆ มีวิธีการสร้าง <math>\boldsymbol{\psi}</math> ที่เป็น 3-CNF ที่ | ||
| + | :::ถ้า <math>\boldsymbol{\phi} \in SAT, \boldsymbol{\psi} \in 3-SAT</math> | ||
| + | :::และถ้า<math>\boldsymbol{\phi} \notin SAT, \boldsymbol{\psi} \notin 3-SAT</math> | ||
| + | ในเวลา Polynomial time<br/> | ||
| + | ตัวอย่างที่ 1 | ||
| + | :::<math>\boldsymbol{\phi} = (X_1 \lor X_2 \lor \neg X_3 \lor X_4)</math> | ||
| + | ให้ใช้วิธีการเพิ่มตัวแปร <math>Z_1</math> จะเปลี่ยนไปอยู่ในรูป | ||
| + | :::<math>\boldsymbol{\psi} = (X_1 \lor X_2 \lor Z_1) \land (\neg X_3 \lor X_4 \lor \neg Z_1)</math> | ||
| + | ตัวอย่างที่ 2 | ||
| + | :::<math>\boldsymbol{\phi} = (X_1 \lor X_2 \lor \neg X_3 \lor X_4 \lor \neg X_5)</math> | ||
| + | ให้ใช้วิธีการเพิ่มตัวแปร <math>Z_1, Z_2</math> จะเปลี่ยนไปอยู่ในรูป | ||
| + | :::<math>\boldsymbol{\psi} = (X_1 \lor X_2 \lor \neg Z_1) \land (Z_1 \lor \neg X_3 \lor \neg Z_2) \land (Z_2 \lor X_4 \lor \neg X_5)</math> | ||
| + | <br/> | ||
| + | '''Note : '''การเติมตัวแปร Z จะต้องเติมแล้วทำให้ค่าความจริงของ <math>\boldsymbol{\phi}</math> equivalence กับค่าความจริงของ <math>\boldsymbol{\psi}</math> | ||
=== ปัญหา Independent Set === | === ปัญหา Independent Set === | ||
| + | นิยาม ให้ Undirected graph G = (V,E) จะกล่าวว่า <math>I \subseteq V</math> เป็น Independent Set ถ้าทุกๆ คู่ของโหนด <math>U, V \subseteq I</math> ไม่มีเส้นเชื่อมกัน<br/> | ||
| + | [[ภาพ:independent_set.jpg]]<br/> | ||
| + | ปัญหา Independent set ให้กราฟ G = (V,E) และ integer k, มี Independent set I ใน G ที่ <math>|I| \ge k</math> หรือไม่ ?<br/> | ||
| + | เราสามารถลดรูปปัญหา 3-SAT ไปเป็นปัญหา Independent set ได้<br/><br/> | ||
| + | <math>3-SAT \le_p </math>Independent set<br/> | ||
| + | ให้ 3-CNF Formular ที่ประกอบด้วย clauses <math>C_1,C_2,...,C_m</math> จะสร้างกราฟ G ดังนี้ | ||
| + | *พิจารณา clause C<sub>1</sub> สร้างโหนด V<sub>11</sub>,V<sub>12</sub>,V<sub>13</sub> สำหรับแต่ละตัวแปรหรือนิเสธของตัวแปรใน C<sub>1</sub><br/> | ||
| + | *เพิ่มเส้นเชื่อม (V<sub>11</sub>,V<sub>12</sub>),(V<sub>11</sub>,V<sub>13</sub>),(V<sub>13</sub>,V<sub>11</sub>)<br/> | ||
| + | *สำหรับโหนดที่แทนตัวแปรกับนิเสธของตัวแปรเดียวกับเพิ่มเส้นเชื่อมระหว่างโหนดเหล่านี้<br/><br/> | ||
| + | :::<math>(X_1 \lor X_2 \lor X_3) \land (\neg X_1 \lor X_2 \lor \neg X_4) \land (X_4 \lor \neg X_3 \lor \neg X_2)</math> | ||
| + | [[ภาพ:3-SAT.jpg]]<br/> | ||
| + | :::ถ้า <math>\boldsymbol{\phi} \in 3-SAT</math> จะมี independence set ขนาด m ใน G | ||
| + | :::ถ้ามี independence set ขนาด m ใน G <math>\Rightarrow \boldsymbol{\phi} \in 3-SAT</math> | ||
| + | |||
| + | == Class NP (Non-deterministic Polynomial time) == | ||
| + | ปัญหา L จะอยู่ใน <math>\mathbb{N}\mathbb{P}</math> ถ้ามี polynomail time algorithm V ที่ <math>\forall x \in L</math> มี certificate P ที่ <math>\left | P \right | = poly \left ( \left | x \right | \right )</math> และ V(x,p) = 1<br/> | ||
| + | แล้ว <math>\forall x \in L</math>, <math>V \left ( x,P \right ) = 1</math> | ||
| + | และ <math>\forall x \notin L</math>, <math>V \left ( x,P \right ) = 0</math><br/> | ||
| + | '''สรุป ปัญหา NP''' คือกลุ่มปัญหาที่สามารถตรวจคำตอบได้ภายใน polynomial time ซึ่งปัญหาง่ายๆ ก็อยู่ใน NP ด้วย<br/> | ||
| + | '''ปัญหา NP-Complete : '''ปัญหา <math>X \in </math>NP-Complete ถ้าสำหรับทุกปัญหา <math>Y \in NP</math> แล้ว <math>Y \le_p X</math><br/> | ||
| + | '''Cook-Lavin Theorem''' -> Proof ว่า SAT เป็น NP-Complete<br/><br/> | ||
| + | :::<math>SAT \le_p 3-SAT \le_p Independent set</math><br/> | ||
| + | สรุป ทั้ง 3-SAT และ independent set เป็น NP-Complete<br/> | ||
| + | '''Note : '''Steps ในการแสดงว่าปัญหา X เป็น NP-Complete คือ <br/> | ||
| + | 1. Proof ว่า <math> X \in NP </math> 2. Proof ว่ามีปัญหา Y ที่เป็น NP-Complete ที่ <math> Y \le_p X </math> | ||
| − | |||
=== ปัญหา Vertex Cover === | === ปัญหา Vertex Cover === | ||
| + | เซต <math>\mathbf{C}</math> เป็น Vertex Corver ของกราฟ <math>\mathbf{G} = (\mathbf{V},\mathbf{E})</math> ถ้า <math>C \subseteq V</math> และทุกๆ edge <math>(U,V) \in E, U \in C</math> หรือ <math> V \in C</math><br/> | ||
| + | ปัญหา Vertex Corver จะให้กราฟ <math>\mathbf{G}</math>, integer k ถามว่า <math>\mathbf{G}</math> มี vertex corver ที่มีขนาด <math>\le</math> k หรือไม่ ?<br\> | ||
| + | *Independent set <math>\le_p</math> Vertex Corver<br\> | ||
| + | **'''Lemma''' พิจารณากราฟ <math>\mathbf{G} = (\mathbf{V},\mathbf{E}), I \subseteq V</math> เป็น Independent Set<br/> | ||
| + | (รูปภาพ) | ||
| + | <br/> | ||
| + | รับกราฟ <math>\mathbf{G}</math> ถามว่ามี independent set <math>\le</math> k ? | ||
| + | สร้าง instance ของ Vertex Corver ที่มีกราฟ <math>\mathbf{G}</math> ถามว่าใน <math>\mathbf{G}</math> มี Vertex Corver ขนาด n-k หรือไม่ ? เมื่อ n = จำนวนโหนดใน <math>\mathbf{G}</math><br\> | ||
| + | <br/> | ||
| + | Vertex Corver เป็น NP Complete เนื่องจากสามารถตรวจได้ว่ากราฟมี Vertex Corver ขนาดไม่เกิน k โดยใช้ Certificate เป็น Vertex Corver นั้น <math>\Rightarrow VC \in NP</math> | ||
=== ปัญหา 3-Color === | === ปัญหา 3-Color === | ||
| + | ให้กราฟ <math>\mathbf{G}</math> ต้องการกำหนดสีให้กับแต่ละโหนด โดยที่คู่ของโหนดที่มีเส้นเชื่อมถึงกันห้ามใช้สีเดียวกัน สามารถทำได้โดยใช้สี <math>\le</math> 3 สีหรือไม่ ?<br/> | ||
| + | [[ภาพ:3-Color.jpg]]<br/> | ||
| + | จะแสดงว่า 3-Color เป็น NP Complete<br/> | ||
| + | 1. แสดงว่า <math>3-Color \in NP</math> | ||
| + | :ใช้การกำหนดสีให้กับแต่ละโหนดเป็น Certificate ตรวจว่า | ||
| + | ::1) ใช้สีไม่เกิน 3 สี | ||
| + | ::2)ไม่มี edge เติมโหนดที่มีปัญหาทำได้ polynomial time | ||
| + | ::ซึ่งสามารถทำได้ใน polynomial time<br/> | ||
| + | 2. แสดงว่า <math>3-Color \le_p 3-SAT</math><br/> | ||
| + | :กำหนดโหนด 3 โหนดแทนสี 3 สี จากนั้นสร้างกราฟดังนี้<br/> | ||
| + | [[ภาพ:3-Color2.jpg]]<br/> | ||
| + | :ถ้าให้ clause <math> X_1 \lor \neg X_2 \lor X_3</math> ต้องสร้างกราฟให้มีตัวใดตัวหนึ่งเป็นจริงและอีก 2 ตัวเป็น false ได้กราฟดังนี้<br/> | ||
| + | [[ภาพ:3-Color3.jpg]]<br/> | ||
| + | :กราฟนี้จะบังคับให้ต้องมีตัวใดตัวหนึ่งเป็น True นั่นคือ <math>3-Color \le_p 3-SAT</math><br/> | ||
รุ่นแก้ไขปัจจุบันเมื่อ 03:14, 7 ตุลาคม 2553
จดบันทึกคำบรรยายโดย:
- นายเกรียงไกร ลิ่มทอง รหัส : 50653732
- นายธีรวัฒน์ ตออำนวย รหัส : 50653815
เนื้อหา
NP Completeness
NP : Non-deterministic Polynomial time ปัญหาที่เป็น NP เป็นปัญหาที่ไม่สามารถแก้ได้ภายใน polynomial time เป็นวิธีหนึ่งที่จะแสดงว่าปัญหาที่กล่าวถึงนั้นยาก แต่ก่อนที่จะกล่าวถึงปัญหาที่อยู่ใน NP Class จะกล่าวถึงปัญหาที่ไม่มีอัลกอริทึมใดแก้ได้ก่อนนั่นคือ ปัญหา Halting problem
Note : ปัญหา Halting problem ไม่ใช่ปัญหาใน NP Class เพราะไม่สามารถแก้ได้
ปัญหา Halting Problem
Description : ให้โปรแกรม P และ input X ถามว่า P(x) ทำงานจบหรือไม่ จะพบว่าเราไม่สามารถออกแบบอัลกอริทึมที่แก้ปัญหานี้ได้ ซึ่งสามารถพิสูจน์โดย contradiction ได้ดังนี้
Proof : สมมติให้มีอัลกอริทึม Q ที่แก้ปัญหา Halting Problem ได้ โดยมี Q(program P, input X) จะ return True ถ้า P(x) halt และ return False เมื่อ P(x) ติด loop เพราะฉะนั้นเราจะสามารถสร้าง procedure Q' ที่มีอัลกอริทึมดังต่อไปนี้ได้
Procedure Q'(program P)
If Q(P, P) then
loop forever
Else
halt
จาก procedure Q' พิจารณา Q'(Q') ว่า halt หรือไม่
Case1 : Q'(Q') halt
นั่นคือ Q(Q',Q') = False --> Q'(Q') = False คือ Q'(Q') ติด loop *Contradict
Case2 : Q'(Q') loop
นั่นคือ Q(Q',Q') = Ture --> Q'(Q') = True คือ Q'(Q') halt *Contradict
เกิด Contradiction จึงสรุปได้ว่าไม่สามารถสร้าง procedure Q' ได้
เพราะฉะนั้น สมมติฐานที่มีอัลกอริทึม Q ที่แก้ปัญหา Halting Problem ได้ ไม่เป็นจริง
Note : ปัญหา Halting problem ถูกพิสูจน์โดย Alan Turing
ปัญหา Program Equivalence
Description : ให้โปรแกรม P1 และ P2 ถามว่า P1 และ P2 ให้ผลลัพธ์เหมือนกันในทุกๆ input หรือไม่ ในที่นี้เราจะพิสูจน์โดยวิธี Reduction จากปัญหา Halting Problem (HP) ไปสู่ปัญหา Program Equivalence (PE)
Proof : สมมติว่ามีอัลกอริทึม Q ที่แก้ปัญหา Program Equivalence ได้
ให้มี procedure HP(P,x) สำหรับแก้ปัญหา Halting Problem
- สร้าง program P' ที่ทำงานเหมือน P(x) แต่ไม่รับ input และไม่มี output แต่ก่อนจบพิมพ์ "done"
- สร้าง program P" ที่ไม่ทำอะไรพิมพ์ "done" อย่างเดียว
- ให้ procedure นี้ return Q(P',P")
เพราะเราสามารถบอกได้ว่า HP(P,x) ไม่สามารถแก้ได้ดังนั้น Q(P',P") ไม่สามารถแก้ได้ด้วยคือ reduction จาก HP ไป PE
- Reduction
- จะแสดงว่าปัญหา X ยาก ถ้าทราบว่าปัญหา Y ยาก จะสามารถบอกได้ว่าปัญหา X ยาก โดย ตั้งสมมติฐานว่าถ้าแก้ปัญหา X ได้จะแก้ปัญหา Y ได้ด้วย ถ้าสามารถพิสูจน์สมมติฐานนี้ว่าเป็นจริงได้ จะสามารถสรุปได้ว่า ปัญหา X แก้ไม่ได้ เพราะปัญหา Y แก้ไม่ได้ เป็นการพิสูจน์แบบ Reduction จาก Y ไป X
Decision Problem
Description : คือปัญหาที่ต้องการคำตอบเป็น Yes หรือ No
ปัญหา Decision Problem P สามารถนิยามใหม่ ด้วย Language P ซึ่งเป็นเซ็ตของ instance ที่ตอบ yes เช่น
Decision Problem
Prime : ให้จำนวนจริง X ถามว่า X เป็น prime หรือไม่
Shortest path : ให้หาว่ามี Shortest path จาก s ไป t ที่ยาวไม่เกิน p หรือไม่
Language
Prime : {3, 5, 7, 11, ...}
Shortest path : {...} (set ของ Shortest path จาก s ไป t ที่ยาวไม่เกิน p)
นิยาม : Problem คือกลุ่มของปัญหา Instance คือตัวปัญหาแต่ละตัว
มีปัญหา A กับ B จะกล่าวว่า A สามารถลดรูป (reducible) ไปยัง B ได้แบบ polynomial time
ถ้ามี function T ทำงานใน polynomial time ที่
- และ
- หรือเขียนอีกอย่างหนึ่งได้ว่า
เขียนแทนด้วย
ถ้าต้องการวัดประสิทธิภาพของ ว่าทำงานเป็น polynomail time ไหม และทราบว่า B ทำงานใน polynomail time ให้หาว่ามี T ที่ทำงานใน polynomail time และเป็นไปตามข้อกำหนดด้านบนไหม แสดงว่า A ทำงานได้ใน polynomail time และเขียนแทนด้วย
ปัญหา Satisfiability (SAT)
นิยาม : CNF formula คือนิพจน์ทางตรรกศาสตร์ที่เขียนให้อยู่ในรูปของการ AND กันของ Clause ที่เป็นการ OR กับของตัวแปรหรือนิเสธของตัวแปร
ตัวอย่างเช่น
ปัญหา SAT คือ กำหนด CNF formula ให้ถามว่า มีวิธีกำหนดค่าให้กับตัวแปรต่างๆ ใน ที่ทำให้ เป็นจริงหรือไม่
Note : Clause ที่เป็นการ OR กับของตัวแปรหรือนิเสธของตัวแปร เรียกว่า Disjunction ตัวอย่างเช่น
ปัญหา 3-Satisfiability (3-SAT)
รับค่า CNF Formula ที่แต่ละ clause มีตัวแปร 3 ตัว ถามว่าทำให้ เป็นจริงได้หรือไม่ ?
- กรณี
ในกรณีนี้เป็นจริงอยู่แล้วเพราะ 3-SAT เป็นกรณีเฉพาะของ SAT แต่เราต้องการพิสูจน์ว่า
plan: แสดงว่าสำหรับ CNF ใดๆ มีวิธีการสร้าง ที่เป็น 3-CNF ที่
- ถ้า
- และถ้า
ในเวลา Polynomial time
ตัวอย่างที่ 1
ให้ใช้วิธีการเพิ่มตัวแปร จะเปลี่ยนไปอยู่ในรูป
ตัวอย่างที่ 2
ให้ใช้วิธีการเพิ่มตัวแปร จะเปลี่ยนไปอยู่ในรูป
Note : การเติมตัวแปร Z จะต้องเติมแล้วทำให้ค่าความจริงของ equivalence กับค่าความจริงของ
ปัญหา Independent Set
นิยาม ให้ Undirected graph G = (V,E) จะกล่าวว่า เป็น Independent Set ถ้าทุกๆ คู่ของโหนด ไม่มีเส้นเชื่อมกัน
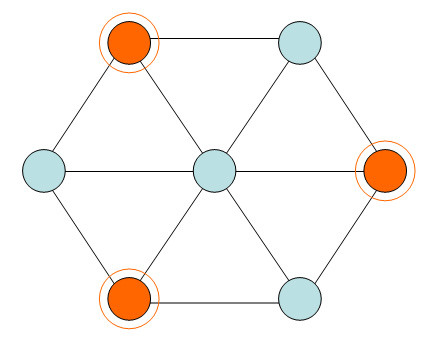
ปัญหา Independent set ให้กราฟ G = (V,E) และ integer k, มี Independent set I ใน G ที่ หรือไม่ ?
เราสามารถลดรูปปัญหา 3-SAT ไปเป็นปัญหา Independent set ได้
Independent set
ให้ 3-CNF Formular ที่ประกอบด้วย clauses จะสร้างกราฟ G ดังนี้
- พิจารณา clause C1 สร้างโหนด V11,V12,V13 สำหรับแต่ละตัวแปรหรือนิเสธของตัวแปรใน C1
- เพิ่มเส้นเชื่อม (V11,V12),(V11,V13),(V13,V11)
- สำหรับโหนดที่แทนตัวแปรกับนิเสธของตัวแปรเดียวกับเพิ่มเส้นเชื่อมระหว่างโหนดเหล่านี้
- ถ้า จะมี independence set ขนาด m ใน G
- ถ้ามี independence set ขนาด m ใน G
Class NP (Non-deterministic Polynomial time)
ปัญหา L จะอยู่ใน ถ้ามี polynomail time algorithm V ที่ มี certificate P ที่ และ V(x,p) = 1
แล้ว ,
และ ,
สรุป ปัญหา NP คือกลุ่มปัญหาที่สามารถตรวจคำตอบได้ภายใน polynomial time ซึ่งปัญหาง่ายๆ ก็อยู่ใน NP ด้วย
ปัญหา NP-Complete : ปัญหา NP-Complete ถ้าสำหรับทุกปัญหา แล้ว
Cook-Lavin Theorem -> Proof ว่า SAT เป็น NP-Complete
สรุป ทั้ง 3-SAT และ independent set เป็น NP-Complete
Note : Steps ในการแสดงว่าปัญหา X เป็น NP-Complete คือ
1. Proof ว่า 2. Proof ว่ามีปัญหา Y ที่เป็น NP-Complete ที่
ปัญหา Vertex Cover
เซต เป็น Vertex Corver ของกราฟ ถ้า และทุกๆ edge หรือ
ปัญหา Vertex Corver จะให้กราฟ , integer k ถามว่า มี vertex corver ที่มีขนาด k หรือไม่ ?<br\>
- Independent set Vertex Corver<br\>
- Lemma พิจารณากราฟ เป็น Independent Set
- Lemma พิจารณากราฟ เป็น Independent Set
(รูปภาพ)
รับกราฟ ถามว่ามี independent set k ?
สร้าง instance ของ Vertex Corver ที่มีกราฟ ถามว่าใน มี Vertex Corver ขนาด n-k หรือไม่ ? เมื่อ n = จำนวนโหนดใน <br\>
Vertex Corver เป็น NP Complete เนื่องจากสามารถตรวจได้ว่ากราฟมี Vertex Corver ขนาดไม่เกิน k โดยใช้ Certificate เป็น Vertex Corver นั้น
ปัญหา 3-Color
ให้กราฟ ต้องการกำหนดสีให้กับแต่ละโหนด โดยที่คู่ของโหนดที่มีเส้นเชื่อมถึงกันห้ามใช้สีเดียวกัน สามารถทำได้โดยใช้สี 3 สีหรือไม่ ?

จะแสดงว่า 3-Color เป็น NP Complete
1. แสดงว่า
- ใช้การกำหนดสีให้กับแต่ละโหนดเป็น Certificate ตรวจว่า
- 1) ใช้สีไม่เกิน 3 สี
- 2)ไม่มี edge เติมโหนดที่มีปัญหาทำได้ polynomial time
- ซึ่งสามารถทำได้ใน polynomial time
2. แสดงว่า
- กำหนดโหนด 3 โหนดแทนสี 3 สี จากนั้นสร้างกราฟดังนี้
- ถ้าให้ clause ต้องสร้างกราฟให้มีตัวใดตัวหนึ่งเป็นจริงและอีก 2 ตัวเป็น false ได้กราฟดังนี้
- กราฟนี้จะบังคับให้ต้องมีตัวใดตัวหนึ่งเป็น True นั่นคือ





















































