ผลต่างระหว่างรุ่นของ "204512/บรรยาย 3"
Jittat (คุย | มีส่วนร่วม) |
|||
| แถว 1: | แถว 1: | ||
{{หัวคำบรรยาย|204512}} | {{หัวคำบรรยาย|204512}} | ||
| + | '''จดบันทึกคำบรรยายโดย:''' ''(กรุณาใส่ด้วย)'' | ||
== ความรู้เบื้องต้น == | == ความรู้เบื้องต้น == | ||
Tree เป็นโครงสร้างชนิดไม่เชิงเส้น (Non-linear) มีลักษณะเป็น recursive ประกอบไปด้วยสมาชิกที่เรียกว่า Node และมีเส้นที่เชื่อมระหว่าง Node ที่เรียกว่า branch คำสำคัญที่เกี่ยวกับ Tree มีดังนี้ | Tree เป็นโครงสร้างชนิดไม่เชิงเส้น (Non-linear) มีลักษณะเป็น recursive ประกอบไปด้วยสมาชิกที่เรียกว่า Node และมีเส้นที่เชื่อมระหว่าง Node ที่เรียกว่า branch คำสำคัญที่เกี่ยวกับ Tree มีดังนี้ | ||
รุ่นแก้ไขเมื่อ 05:12, 9 สิงหาคม 2550
บันทึกคำบรรยายวิชา 204512 นี้ เป็นบันทึกที่นิสิตเขียนขึ้น เนื้อหาโดยมากยังไม่ผ่านการตรวจสอบอย่างละเอียด การนำไปใช้ควรระมัดระวัง
จดบันทึกคำบรรยายโดย: (กรุณาใส่ด้วย)
เนื้อหา
ความรู้เบื้องต้น
Tree เป็นโครงสร้างชนิดไม่เชิงเส้น (Non-linear) มีลักษณะเป็น recursive ประกอบไปด้วยสมาชิกที่เรียกว่า Node และมีเส้นที่เชื่อมระหว่าง Node ที่เรียกว่า branch คำสำคัญที่เกี่ยวกับ Tree มีดังนี้
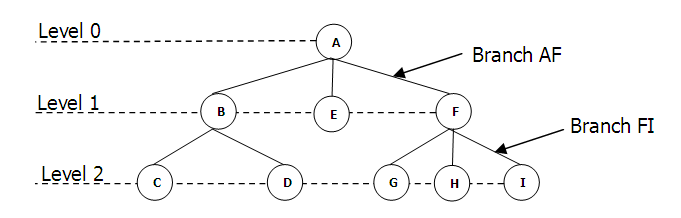
| Root Node: A | Sibling Node: {B, E, F}, {C, D}, {G, H, I} |
| Parents Node: A, B, F | Leaves Node: C, D, E, G, H, I |
| Child Node: B, E, F, C, D, G, H, I | Internal Node: B, F |
- Root Node คือ โหนดที่อยู่บนสุดของต้นไม้
- Leaf Node คือ โหนดที่ไม่มีลูกหรือโหนดอื่นต่อ เรียกอีกอย่างหนึ่งว่า External Node
- Internal Node คือ โหนดที่ไม่ใช่ Root และ Leaf Node
- Depth คือ ความยาวจาก Root node ถึง Node ที่สนใจ
- Height คือ ความยาวจาก Node ที่สนใจถึง Leaf Node ที่ลึกที่สุดที่มี Node ที่สนใจเป็น Parent
Binary Search Tree
Binary Search Tree คือ Data Structure ที่ define แบบ Recursive โดยขั้นตอนวิธีการทำงานที่สำคัญของ Binary Tree จะสนับสนุนการทำงานดังต่อไปนี้
- Find (key)
- Insert (key)
- Delete (key)
ซึ่งเวลาที่ใช้ในการค้นหานั้นจะขึ้นอยู่กับความสูงของต้นไม้ โดยถ้ามีข้อมูล n ตัวความสูงของต้นไม้จะไม่ลึกไปกว่า O(log n) ถ้าสูงกว่าจะทำให้เกิด Worse-case
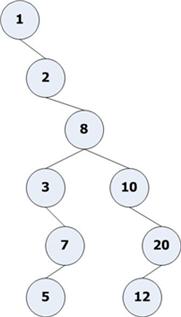
สมมติว่ามี data 1,2,8,3,7,5,10,20,12 เขียนเป็น Binary Search Tree ได้ดังนี้
AVL Tree
AVL (Adelson-Velskii and Landis) tree คือ binary search tree ที่มีเงื่อนไขของความสมดุล (Balance Condition) โดยเงื่อนไขดังกล่าวคือ
Condition: ในทุกๆ โหนด ความสูงของ subtree ทางด้ายซ้ายและด้านขวาต่างกันไม่เกิน 1 โดยที่ให้ N(k) แทนจำนวนโหนดที่น้อยที่สุดใน AVL Tree ที่มีความสูง k
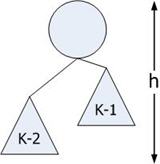
จากเงื่อนไขของ AVL Tree จะสรุปได้
N(1) = 1, N(2) = 2
N(k) = N(k-1) + N(k-2) + 1
จะสังเกตได้ว่ามีลักษณะเป็น Fibonacci แต่มีการบวก 1 เข้ามาด้วย
จากสมการข้างต้น
N(k) = N(k-1) + N(k-2) + 1
N(k) = N(k-2) + N(k-3) + N(k-2) + 1
≥ 2N(k-2)
≥
≥ ---*
จะสังเกตได้ว่าฟังก์ชันดังกล่าวมีขนาดเป็น Exponential ใน k
สรุป: AVL Tree ที่มี n โหนดจะมีความสูง O(log n)
การหมุนของ AVL Tree
การหมุน (Rotation) ของ AVL Tree กระทำเพื่อให้ต้นไม้ที่ไม่อยู่ในเงื่อนไขของ AVL Tree กลับเข้ามาอยู่ในเงื่อนไข ซึ่งมีรูปแบบการทำงานดังนี้
- Single Rotation
- การหมุนทางขวา (Right Rotation)
- การหมุนทางซ้าย (Left Rotation)
- Double Rotation
การหมุนทางขวา (Right Rotation)
จะกระทำเมื่อทางด้านซ้ายของต้นไม้มีความสุงกว่าด้านขวาเกิน 1 ซึ่งไม่ตรงตามเงื่อนไขของ AVL Tree จึงใช้การกระทำที่เรียกว่า “การหมุนทางขวา” เพื่อทำให้ตรงตามเงื่อนไขดังกล่าว

การหมุนทางซ้าย (Left Rotation)
ในทางกลับกันถ้าหากทางด้านขวาของต้นไม้มีความสูงไม่สัมพันธ์กับเงื่อนไขของ AVL Tree จะทำการหมุนทางซ้ายเพื่อให้ต้นไม้กลับมาสมดุล
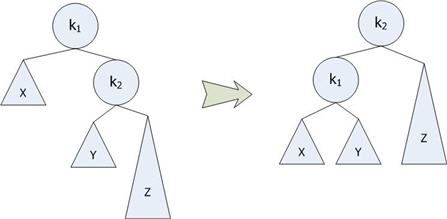
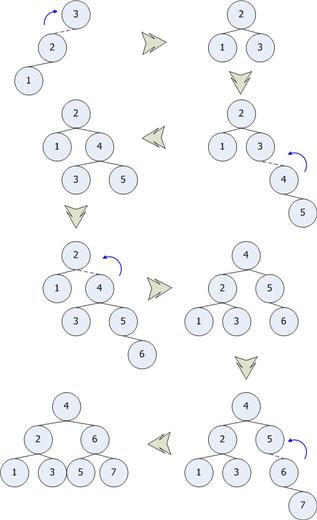
ตัวอย่าง Single Rotation โดยการใส่ตัวเลข 1 – 7 ตามลำดับ
การ Double Rotation
ในบางครั้งการหมุนสามารถทำการหมุนได้หลาย ครั้งเช่น เมื่อทำการหมุนซ้ายแล้วทำการหมุนขวา หรือทำการหมุนขวาแล้วหมุนซ้าย โดยอาศัยเทคนิคการหมุนทางซ้ายและทางขวาร่วมกัน
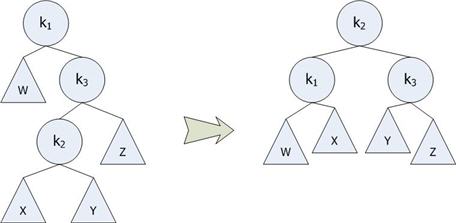
ตัวอย่าง Double Rotation โดยการใส่ตัวเลข 14 เข้าไปในต้นไม้
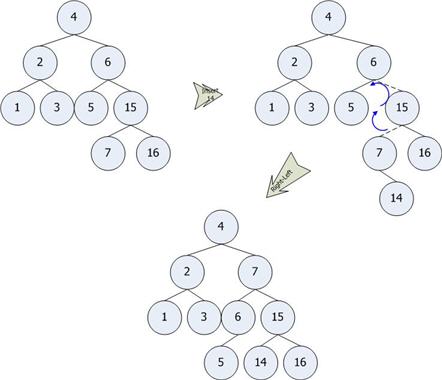
Amortized Analysis
เป็นการคิดการชาร์จเวลาการทำงานในการทำงานในส่วนกิจกรรมย่อยๆ เพื่อนำมาใช้ทดแทนกิจกรรมอื่นในภายหลัง ยกตัวอย่างเช่น การทำงานกับ Variable Array เมื่อ insert ข้อมูลเต็ม array แล้ว เราต้องทำการเพิ่ม array แล้วทำการคัดลอก array เก่า
สมมุติมี array 1 ชุดเมื่อมีการเต็มข้อมูลเต็มแล้วก็จะมีการจอง array ใหม่แล้วคัดลอกข้อมูลของเดิมมาเก็บที่ไหม่ ดังนั้นถ้ามีข้อมูล n ตัว จะต้องใช้เวลาถึง O(n²)
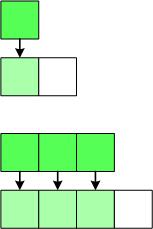
แต่เมื่อเราใช้การคิดเวลาแบบ Amortized แล้ว เราสามารถคิดแบบเวลาที่ทำทั้งหมด โดยใช้เวลาไม่เกินเท่าไร ซึ่งมีการคิดเวลาล่วงหน้าและมีการจองพื้นที่ array เป็นสองเท่าจากข้อมูลที่มีอยู่
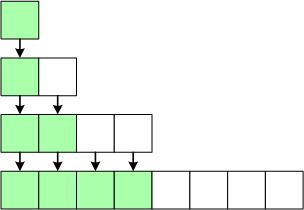
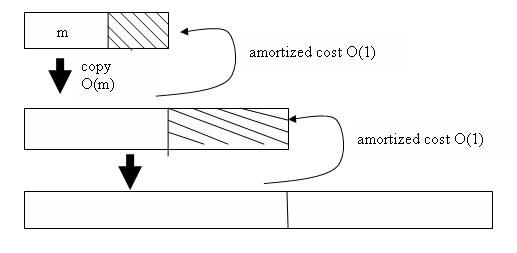
ซึ่งสามารถสรุปเป็นกราฟได้ดังภาพ

Claim: Variable array เมื่อมีการเพิ่มข้อมูลไป m ครั้งจะใช้เวลาทำงาน O(m) โดย amortized running time ของการเพิ่มข้อมูลคือ O(1)
Proof: ในการคิดเวลาการทำงานล่วงหน้าของการเพิ่มข้อมูลแต่ละคั้งคิดเป็น 3 หน่วย โดยถ้าในเวลาที่ทำการเพิ่มข้อมูลโดยไม่มีการเพิ่มขนาดของ array จะมีการใช้เวลาในการทำงานจริง 1 หน่วย ซึ่งดังนั้นจะเหลือเวลาอีก 2 หน่วย แต่ในกรณีที่มีการขยายขนาดของ array จาก 2i เป็น 2i+1 จะมีการเพิ่มข้อมูลที่ไม่มีการ array 2i-1
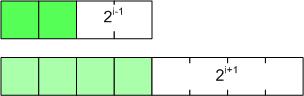
จะใช้เวลา 2 x 2i-1 = 2i
ดังนั้น การเพิ่มข้อมูล m ครั้ง ใช้เวลา 3m = O(m) หน่วย
Delete Tree
การลบ Node ในต้นไม้มีวิธีการลบแบบหนึ่งที่เรียกว่า Lazy Delete มีวิธีการทำงานคือจะใช้การ Mark โหนดแทนการลบโหนดออกจากต้นไม้ โดยวิธีนี้จะเกิดปัญหาเมื่อมีการลบและ insert โหนดหลายๆครั้ง ส่งผลให้ต้นไม้มีความสูงมาก และไม่สามารถทำงานได้ภายในเวลา O(log n) เมื่อ N ≤ 2n ; N คือโหนดที่ถูกลบ
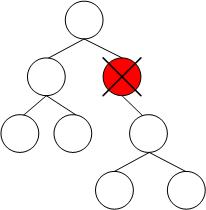
ในกรณีที่ N > 2n จะต้องมีการสร้างต้นไม้ขึ้นมาใหม่ โดยจะนำ Data ออกมาทั้งหมดและ Insert เข้าไปใหม่ ใช้เวลาทำงาน O(n)
จากข้างต้น กราฟในการทำงานของ Lazy Delete จะ peak เป็นช่วงๆ ซึ่งช่วงที่ peak จะเป็นช่วงที่มีการลบโหนด และเวลาในการทำงานจะคิดเฉลี่ยตามแบบการทำงานของ Amortized Analysis
Scapegoat Tree
จากแนวคิดของ amortized analysis เราสามารถวิเคราะห์ต้นไม้ที่เรียกว่า Scapegoat โดยที่ AVL Tree นั้นรับประกันว่าการทำงานในแต่ละครั้งจะมีเวลาการทำงานไม่เกิน O(n) แต่ใน Scapegoat Tree จะมีเงื่อนไขที่แตกต่างไป
สำหรับ node v ในต้นไม้, ให้ แทน subtree ที่มี Root เป็น v ให้ left(v) แทนลูกด้านซ้ายของ v, right(v) แทนลูกด้านขวาของ v และ แทนจำนวนโหนดใน
เงื่อนไขความสมดุลย์ของ scapegoat tree เป็นดังนี้
Condition: สำหรับทุก ๆ โหนด v,
และ
เงื่อนไขดังกล่าว รับประกันความสูงของต้นไม้ ดังที่แสดงใน claim ต่อไปนี้
Claim: Scapegoat tree ที่มี n โหนดจะมีความลึกไม่เกิน O(log n)
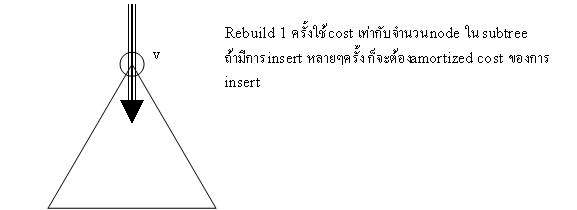
Operation: Insert node การ Insert node ใหม่ใส่ใน Scapgoat trees จะมีลักษณะการ Insert ตามปรกติเหมือน Binary Search trees ซึ่งเป็นการใส่ node ใหม่ลงไปใน tree แบบ inorder ก็จะได้ลำดับที่เรียงแล้วในเวลา linear time แต่เมื่อมีการ insert node ใหม่เข้าไปใน Scapgoat trees เรื่อยๆ แล้วถ้าพบ node v ที่ h(v) > log |v| จะต้องทำการ rebuild subtrees ที่ v ใหม่โดยใช้เวลาในการ rebuild O(|v|)
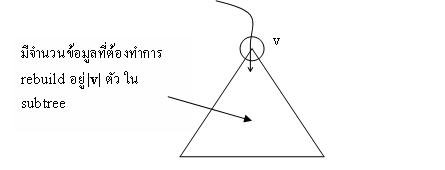
ถ้าหาก Scapgoat trees นั้นไม่ balance ที่ node ที่อยู่ด้านบนของ node v อีกก็จะต้องเสีย time มาก ในการที่จะกลับไป balance ที่ node ด้านบนต่อ ซึ่งทำให้มี cost ของการ balance สูงมาก เราจะ amortize ไปที่การ insert หลายๆ ครั้งเพื่อให้มี cost ดีที่สุด
จากการ Amortize Analysis ที่ผ่านมา Operation: Insert node การ Insert node ใหม่ใส่ใน Scapgoat trees จะมีลักษณะการ Insert ตามปรกติเหมือน Binary Search trees ซึ่งเป็นการใส่ node ใหม่ลงไปใน tree แบบ inorder ก็จะได้ลำดับที่เรียงแล้วในเวลา linear time แต่เมื่อมีการ insert node ใหม่เข้าไปใน Scapgoat trees เรื่อยๆ แล้วถ้าพบ node v ที่ h(v) > log |v| จะต้องทำการ rebuild subtrees ที่ v ใหม่โดยใช้เวลาในการ rebuild O(|v|)
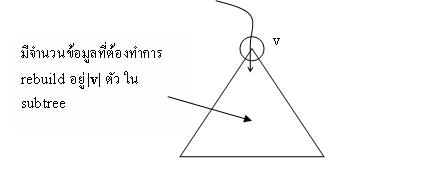
ถ้าหาก Scapgoat trees นั้นไม่ balance ที่ node ที่อยู่ด้านบนของ node v อีกก็จะต้องเสีย time มาก ในการที่จะกลับไป balance ที่ node ด้านบนต่อ ซึ่งทำให้มี cost ของการ balance สูงมาก เราจะ amortize ไปที่การ insert หลายๆ ครั้งเพื่อให้มี cost ดีที่สุด
จากการ Amortize Analysis ที่ผ่านมา
ถ้าที่ node v
Claim: ก่อนการ rebuild ใดๆ ที่node v จะมีการ insert เข้าไปใน subtree ทื่node v ไม่น้อยกว่า (|v|) ครั้ง
ถ้าต้องการ insert เข้าไป ต้องเตรียม amortized cost O(1) ต่อการ insert 1 ครั้ง ดังนั้นการ rebuild ที่ |v| ครั้ง เราสามารถ charge O(1) ไปที่ node ที่ถูก insert เข้าไปใน subtree ที่ node v เป็น root ได้
สังเกตว่า node ใดๆ ที่ถูก insert ไปจะโดน charge ไม่เกิน log n ครั้ง ดังนั้น cost ของการ insert + charge ของการ rebuild เท่ากับ O( log n ) ซึ่งเท่ากับ O( log n ) นั่นเอง
Prof of Claim:
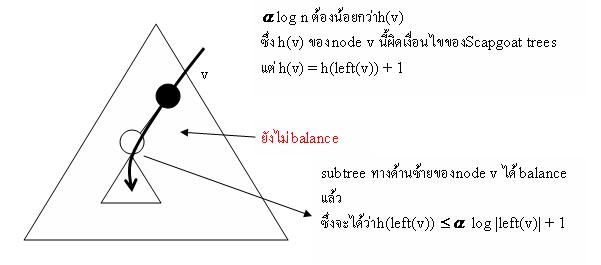

ดังนั้น
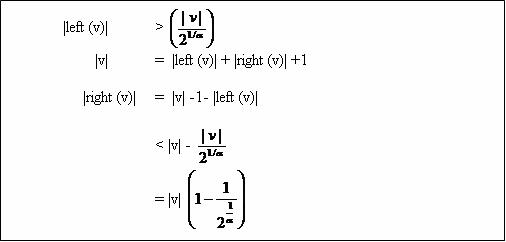
เราจะได้ข้อสรุปว่า เมื่อเรา rebuild ครั้งสุดท้ายแล้วจำนวน node ของ subtree ทางซ้ายและจำนวน node ของ subtree ทางขวาต่างกันอย่างมาก 1 node

ทบทวนความรู้เรื่อง Experiment, Expected value, Random variable
Experiment
- Event คือ เหตุการณ์ที่สนใจ
- Outcome คือ ผลลัพธ์ของเหตุการณ์ที่สนใจเป็น sub set ของ Sample space
- Sample space คือ set ของ outcome ที่เป็นไปได้
- Probability คือ ความน่าจะเป็น หมายถึง โอกาสที่จะเกิดเหตุการณ์ที่สนใจจากการทดลองสุ่มหนึ่งๆ เป็นจำนวนหรือค่าที่ไม่มีหน่วย เขียนแทนด้วย Pr(?) โดยที่ ? แทนด้วยชื่อของเหตุการณ์ที่สนใจ เช่น Pr [x=5] คือ ความน่าจะเป็นที่ x=5
สำหรับ ![]() โดยที่ A แทน Event เซตของ outcome จะได้ว่า
โดยที่ A แทน Event เซตของ outcome จะได้ว่า
1. ![]()
2. สำหรับ ![]()
3. สำหรับ ![]() ที่ disjoint กัน
ที่ disjoint กัน ![]()
ตัวอย่าง สมมุติให้มีถัง 3 ถัง
ให้ที่ถังแรกไม่มีลูกบอลหล่นลงไปเลย หาความน่าจะเป็น(Pr) ที่จะไม่มีลูกบอลหล่นลงในถังแรก
Ai คือ event ที่ลูกบอลลูกที่ i ไม่หล่นลงในถังใบแรก
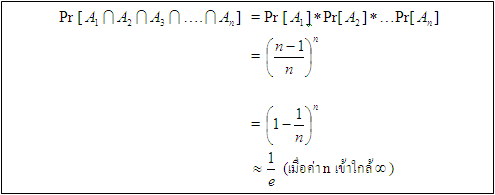
===Random Variable (ตัวแปรสุ่ม)=== คือ function หรือตัวแปรที่มีค่าขึ้นกับผลลัพธ์ (sample space) โดยจะรู้ค่าหลังจากการทดลอง
===Expected value (ค่าคาดหวัง)=== คือค่าเฉลี่ย โดยเฉลี่ยมีค่าเท่าไหร่ weight ตามความน่าจะเป็นที่จะได้ค่านั้น แทนด้วย E
นิยาม ตัวแปรสุ่ม X,![]()
ตัวอย่าง ถ้ามีถัง 3 ถัง บอล 2 ลูกสีดำ และสีขาว

หา Pr[X = i] จะได้ว่า

เอามาเป็นค่า weight ในการคำนวณ




