ผลต่างระหว่างรุ่นของ "204512/บรรยาย 8"
Top (คุย | มีส่วนร่วม) |
Top (คุย | มีส่วนร่วม) |
||
| แถว 49: | แถว 49: | ||
อัลกอริทึมสำหรับหา maximum flow ของ Dinic ประกอบด้วยการตั้งค่าเริ่มต้นให้ flow เป็นศูนย์ และทำขั้นตอน blocking step ซ้ำไปเรื่อยๆจนโหนด ''t'' ไม่อยู่ใน level graph โดยขั้นตอน blocking step จะแสดงต่อไปนี้ | อัลกอริทึมสำหรับหา maximum flow ของ Dinic ประกอบด้วยการตั้งค่าเริ่มต้นให้ flow เป็นศูนย์ และทำขั้นตอน blocking step ซ้ำไปเรื่อยๆจนโหนด ''t'' ไม่อยู่ใน level graph โดยขั้นตอน blocking step จะแสดงต่อไปนี้ | ||
BLOCKING STEP(Dinic) : | BLOCKING STEP(Dinic) : | ||
| + | |||
ให้ <math>f\,</math> เป็น flow ปัจจุบัน และ <math>G_f\,</math> เป็น residual graph | ให้ <math>f\,</math> เป็น flow ปัจจุบัน และ <math>G_f\,</math> เป็น residual graph | ||
| − | + | 1 หา level graph <math>L\,</math> ของ <math>G_f\,</math> | |
| − | + | 2 หา blocking flow <math>f'\,</math> ใน <math>L\,</math> | |
| − | + | 3 ปรับ <math>f\,</math> ให้เป็น <math>f+f'\,</math> | |
รุ่นแก้ไขเมื่อ 08:21, 7 สิงหาคม 2550
บันทึกคำบรรยายวิชา 204512 นี้ เป็นบันทึกที่นิสิตเขียนขึ้น เนื้อหาโดยมากยังไม่ผ่านการตรวจสอบอย่างละเอียด การนำไปใช้ควรระมัดระวัง
การบรรยายครั้งนี้จะกล่าวถึงการแก้ปัญหา network flows โดยใช้แนวคิดเกี่ยวกับ blocking flows ซึ่งนำไปสู่อัลกอริทึมของ E.A.Dinic
Blocking Flows
สำหรับการนิยาม blocking flows เราจะต้องให้นิยาม saturated edge ก่อน
- นิยาม 8.1
- ให้ network G และ flow f จะกล่าวว่า edge e saturated (อิ่มตัว) ถ้า f ใช้ capacity ของ e จนหมด นั่นคือ
และเราสามารถนิยาม blocking flows ได้ดังนี้
- นิยาม 8.2
- เราจะเรียก flow f ว่าเป็น blocking flow ถ้า ทุกๆ s-t path มี saturated edge อย่างน้อยหนึ่ง edge
จะเห็นว่าถ้า f เป็น blocking flow แล้ว เราไม่สามารถเพิ่มขนาดของ flow โดยการดัน flow เพิ่มตาม path ใน G ได้อีก เนื่องจากทุก path มี saturated edge อยู่ แต่เราอาจเพิ่มขนาดของ flow ได้โดยการลด flow บน edge บางเส้น และเพิ่มไปยัง edge อื่น พิจารณาตัวอย่างต่อไปนี้
- ตัวอย่าง 8.1
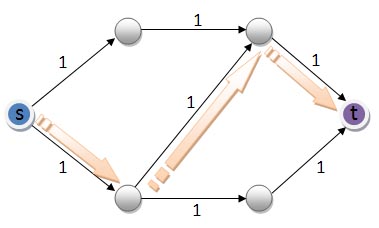
- ให้กราฟมีทิศทางดังรูปที่ 8.1 โดย edge ทุกๆเส้นมี capacity เท่ากับ 1
รูปที่ 8.1 ตัวอย่าง blocking flow
พิจารณา flow f ที่มีขนาดเท่ากับ 1 ตามลูกศรสีส้มในรูป จะเห็นว่า edge ทั้งสามเส้นที่มี flow f ไหลผ่าน เป็น saturated edge ทั้งสิ้น และทุกๆ path จาก s ไปยัง t จะมี saturated edge อย่างน้อยหนึ่งเส้น ซึ่งทำให้เราไม่สามารถเพิ่ม flow ตาม path เหล่านี้ได้อีก ดังนั้น f ในตัวอย่างนี้เป็น blocking flow
Level Graphs
ในอัลกอริทึมของ Dinic จะมีขั้นตอนการหา blocking flow บนกราฟที่มีลักษณะพิเศษบางอย่าง ซึ่งเรียกว่า level graph แต่ก่อนจะนิยาม level graph ได้เราต้องให้นิยาม level ของแต่ละโหนดในกราฟก่อน
- นิยาม 8.3
- ให้ต้นทาง s, สำหรับโหนด v ใดๆในกราฟ l(v) คือระยะทางที่สั้นที่สุดจาก s ไปยัง v โดยระยะทางบน path p หมายถึงจำนวน edge บน path p
ต่อมาเราจะสามารถนิยาม level graph ได้ดังนี้
- นิยาม 8.4
- level graph ของกราฟ G คือสับกราฟของ G ที่มีเฉพาะ edge (u,v) ที่
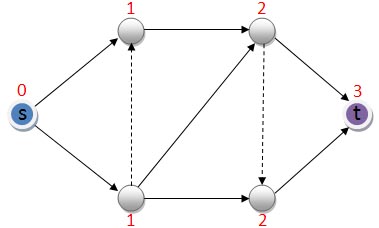
- ตัวอย่าง 8.2
รูปที่ 8.2 ตัวอย่าง level graph
พิจารณากราฟ G ในรูปที่ 8.2 โดย edge ทุกเส้นในรูปอยู่ใน G level graph ของ G จะเป็นกราฟที่มีเฉพาะ edge ที่เป็นเส้นทึบในรูป ค่า level ของแต่ละโหนดถูกแสดงด้วยตัวเลขสีแดง
Dinic's Blocking Flow Algorithm
อัลกอริทึมสำหรับหา maximum flow ของ Dinic ประกอบด้วยการตั้งค่าเริ่มต้นให้ flow เป็นศูนย์ และทำขั้นตอน blocking step ซ้ำไปเรื่อยๆจนโหนด t ไม่อยู่ใน level graph โดยขั้นตอน blocking step จะแสดงต่อไปนี้
BLOCKING STEP(Dinic) : ให้ เป็น flow ปัจจุบัน และ เป็น residual graph 1 หา level graph ของ 2 หา blocking flow ใน 3 ปรับ ให้เป็น