ผลต่างระหว่างรุ่นของ "204512/บรรยาย 14"
Orion else (คุย | มีส่วนร่วม) |
Orion else (คุย | มีส่วนร่วม) |
||
| แถว 58: | แถว 58: | ||
== Traveling Sale person problem == | == Traveling Sale person problem == | ||
| + | ;พื้นฐาน: มีเมือง n เมือง 1,…,n ระหว่างเมือง i กับ j มีระยะทาง d(i,j) โดยที่ d เป็น metric ซึ่งมีเงื่อนไขดังต่อไปนี้<br>(1) d(i,j) = 0 ;∀i หากเป็นจุดเดียวกันระยะทางเป็นศูนย์<br>(2) d(i,j) = d(j,i) ; ∀i,j จุดต้นและปลายเดียวกันไปมาหากันระยะทางเท่ากัน<br>(3) d(i,j) ≤ d(i,k) + d(k,j) ; ∀i,j,k เส้นทางใหม่ ระยะทางไม่ยาวเกินไปกว่าระยะทางเดิม<br>โดย TSP ต้องการหา Cycle ที่ผ่านครบทุกเมือง เมืองละ 1 ครั้งเท่านั้น | ||
| + | |||
| + | |||
| + | |||
| + | <center> [[ภาพ:007-SteinerTree06.JPG|500px|กลไกSteiner]] </center> | ||
| + | |||
== Set Cover problem == | == Set Cover problem == | ||
== Minimum Congestion Routing problem == | == Minimum Congestion Routing problem == | ||
รุ่นแก้ไขเมื่อ 05:00, 2 ตุลาคม 2550
จดบันทึกคำบรรยายโดย:
- นายดิเรก ยิ้มละมัย รหัส : 50653799
วางโครงเฉยๆ อ่ะครับ จะรีบทำให้เสร็จเร็วๆนะครับ
เนื้อหา
Approximation Algorithm
- เนื่องจากการดำเนินการด้วย Algorithm ตรงๆ นั้นหากทำให้เสร็จโดยสมบูรณ์จะมีระยะเวลามากกว่า polynomial time ดังนั้นจึงมี approximation algorithm ด้วยการใช้ heuristic บางอย่างมาช่วยในการดำเนินการ แต่จะไม่รับประกันว่าค่าคำตอบนั้นดีที่สุด
Vertex Cover problem
ให้กร๊าฟ G = (V, E) หา set C ⊆ ที่ Cover edge ทั้งหมด ที่มีขนาดเล็กที่สุด แนวคิดแรก หาก node ที่มี edge เข้าหาตัวมันมากที่สุด Degree มาก แต่จะได้ความห่างจากคำตอบที่ดีที่สุดคือ log(n) แนวคิดที่ดีกว่า หยิบ edge แทนจะทำให้ได้ Node 2 node ในการหยิบหนึ่งครั้งได้ความห่างอยู่ที่ 2 เท่าของคำตอบที่ดีที่สุด วิธีการคร่าวๆ ดังรูป
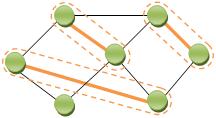
- Algorithm
- C <- ø
While มี edge ใน G
เลือก edge e = (u, v) ใดๆ
C <- C υ {u, v}
ลบทุกๆ Edge ที่ติดกับ u หรือ v
[ M <- M υ {e} ] //ใส่เพื่อ analysis ว่าเป็น edge ร่วมที่เลือก
return C
- Claim
- สำหรับ vertex cover C’ ใดๆ
|C’| ≥ |M| - Proof
- เนื่องจาก C’ เป็น vertex cover ทุกๆ edge e Є M, C’ จะต้องมีจุดปลายของ e อย่างน้อย 1 จุด
อย่างไรก็ตามทุกๆ edge ใน M ไม่ใช่จุดปลายร่วมกันเลยนั่นคือ |C’| ≥ |M| ตามต้องการ ----#
เพราะฉะนั้น Approximate ไม่เกิน 2 เท่า - คำอธิบาย
- edge เหล่านี้สังเกตดีๆ ว่าจะไม่ share node กันเลย จะใช้ cover อย่างน้อยเท่ากับจำนวน edge เหล่านี้ ในแต่ละ edge มี 2 node จะต้องเลือก 1 node เราเลือก edge ทำให้บอกได้ว่าดีที่สุดคือ vertex cover มีค่าเท่ากับจำนวน edge แต่เราเอกได้ 2 node ต่อ 1 edge ดังนั้นคำตอบที่ได้จะเป็น 2 เท่าของ edge
เพราะฉะนั้น คำตอบจะเป็น 2 เท่าของคำตอบจริง
Metric Steiner Tree problem
Steiner tree คือ ปัญหาที่เรามี Complete graph G = (V, E) มี edge weight W(e) บนเส้นเชื่อม e มี Set T ⊆ V หากมองถึง Minimum spanning tree คือหา ทุกๆ node เชื่อมกันที่มี Weight ต่ำที่สุด แต่ในส่วนของ Steiner tree นั้นจะหา Minimum Steiner tree ขอเรียกว่า Minimum Cost Tree ที่ Span T (Steiner Tree)
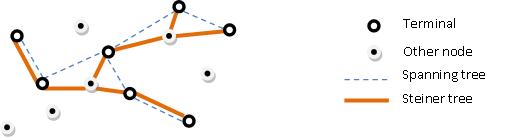
เราสามารถนำโหนดอื่นๆ มาช่วยในการหาได้ เพราะความจริงเราหา minimum spanning tree ไม่ได้จริงในทุก graph แต่เราอยากหาเส้นทางที่ไปได้และใกล้เคียง
หากใช้ Minimum spanning tree เราจะถือว่าทุกโหนดสำคัญ ซึ่งทำให้อาจได้ค่าจาก A, B, C, D เดินหากันนั้นไกลมาก ทั้งที่อยู่ใกล้กันมาก ดังรูป
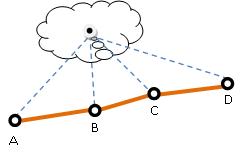
- Algorithm
- สร้างกร๊าฟ G’ ที่ มี T เป็นเซตของโหนด
มี Cost เหมือนเดิม
โดยไม่สนใจโหนดภายนอกโยนทิ้งทั้งหมด คือ การไม่สนโหนดช่วยเหลือ
หา MST G’ (ค่าไม่เกินสองเท่าของ Steiner tree)
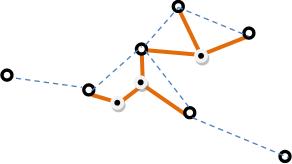
จะพิสูจน์ว่า minimum spanning tree หาได้ค่าดีที่สุดไม่เกินสองเท่าของ Minimum Steiner Tree พิจารณา Optimal Steiner Tree
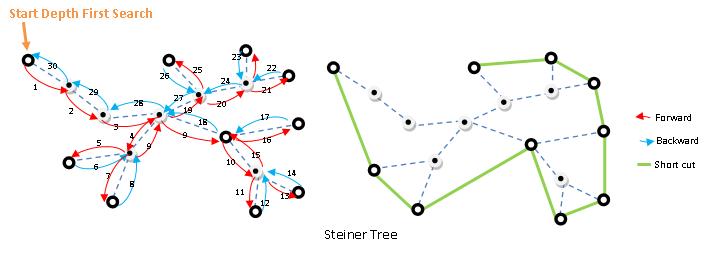
Depth First Search Animation:: http://www.rci.rutgers.edu/~cfs/472_html/AI_SEARCH/SearchAnimations.html
- การสร้าง Steiner Tree ใดๆ สามารถหาได้จาก Spanning ที่มีค่าไม่เกน2เท่าของ Optimum
จะสร้าง F’ ที่เป็น Spanning Tree บน F ที่มี Cost(F’) ≤ 2.Cost(F)
- ขั้นตอนการทำงานจากรูป Steiner Tree ด้านบน
- 1) จาก F สร้าง Trail H ด้วย DFS ความยาวของ H = 2.Cost(F) เพราะแต่ละ Edge ใน F ถูกเดินผ่าน 2 ครั้ง
2) สร้าง F’ จาก H โดยการสร้าง Short cut จะได้ว่า
Cost(F’) ≤ ความยาวของ H = 2.Cost(F)
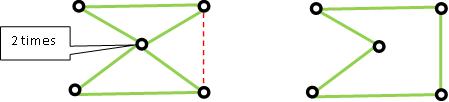
Minimum Steiner Tree มี Span ที่ Cost ไม่เกิน 2 เท่าของ Steiner Tree ทำให้ได้ค่าดีที่สุดไม่เกิน 2 เท่าของ Minimum Steiner Tree แต่ก็ยังมีตัวอย่างที่ MST G’ ให้คำตอบ 2 เท่า
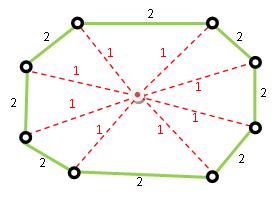
- จากรูป
- 1) จะเป็นการเชื่อมแบบ Completed Graph และ ทุก Edge ความยาว 2 ทำให้ Spanning Tree ตอบ 2(n-1)
2) จากนั้นเติมโหนดสีแดง จะไม่เปลี่ยนค่า Cost ของการเดิน เพราะจะยังคงค่าความยาว 2 เท่าเดิม และเรามีค่า Steiner คือ n โหนด
จะพบว่าเราได้ 2(n-1)/n ซึ่งยิ่งค่า n มากๆ ค่าก็จะเป็นค่าที่เข้าใกล้ 2
Traveling Sale person problem
- พื้นฐาน
- มีเมือง n เมือง 1,…,n ระหว่างเมือง i กับ j มีระยะทาง d(i,j) โดยที่ d เป็น metric ซึ่งมีเงื่อนไขดังต่อไปนี้
(1) d(i,j) = 0 ;∀i หากเป็นจุดเดียวกันระยะทางเป็นศูนย์
(2) d(i,j) = d(j,i) ; ∀i,j จุดต้นและปลายเดียวกันไปมาหากันระยะทางเท่ากัน
(3) d(i,j) ≤ d(i,k) + d(k,j) ; ∀i,j,k เส้นทางใหม่ ระยะทางไม่ยาวเกินไปกว่าระยะทางเดิม
โดย TSP ต้องการหา Cycle ที่ผ่านครบทุกเมือง เมืองละ 1 ครั้งเท่านั้น