ผลต่างระหว่างรุ่นของ "VC-SNDP:spider decomposition"
ไปยังการนำทาง
ไปยังการค้นหา
Jittat (คุย | มีส่วนร่วม) |
Jittat (คุย | มีส่วนร่วม) |
||
| แถว 1: | แถว 1: | ||
This page describes '''spider decompositions''' and the approach of CK and ChK. | This page describes '''spider decompositions''' and the approach of CK and ChK. | ||
| − | ให้กราฟ <math>G=(V,E)</math> เซตของ terminals | + | ให้กราฟ <math>G=(V,E)</math> เซตของ terminals ''T'' และจำนวนเต็มบวก <math>k</math> เรียกโหนดใน ''T'' ว่าเป็น black vertices, นอกจากนั้นเป็น white vertices. |
| − | '''Spider''' คือ | + | '''Spider''' คือ tree ที่มีโหนดที่มีดีกรีมากกว่าสองไม่เกิน 1 จุดยอด ถ้ามี vertex ดังกล่าว จะเรียกว่าเป็น '''head''' ถ้าไม่มี spider จะเป็น path และจะสามารถเรียกโหนดใดเป็น head ก็ได้; เรียกจุดยอดที่ไม่ใช่ leaf และ head ว่า '''intermediate vertex''', เรียก leaf ว่า '''foot''', เรียก path จาก head ไป leaf ว่า '''leg''' |
| − | + | ||
| − | + | == Decomposition == | |
| − | + | ||
| + | ChK แสดงว่า ให้กราฟ G ที่ทุก ๆ คู่ของจุดยอดสีดำ ''k''-element connected, มีสับกราฟ ''H'' ของ ''G'' ที่สามารถ partition เป็น spiders ที่ | ||
| + | # ทุก ๆ leaf เป็น black vertex | ||
| + | # ทุก ๆ black vertex เป็น leg ของ ''k'' spiders พอดี | ||
| + | # ทุก ๆ intermediate vertex เป็น white vertex (สังเกตว่า head เป็น black vertex ได้) | ||
| + | |||
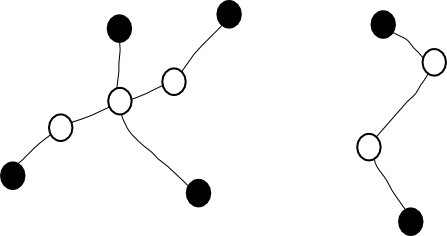
| + | ด้านล่างแสดงตัวอย่างของ spiders | ||
| − | |||
[[ภาพ:Spiders.png]] | [[ภาพ:Spiders.png]] | ||
รุ่นแก้ไขเมื่อ 05:21, 24 กุมภาพันธ์ 2552
This page describes spider decompositions and the approach of CK and ChK.
ให้กราฟ เซตของ terminals T และจำนวนเต็มบวก เรียกโหนดใน T ว่าเป็น black vertices, นอกจากนั้นเป็น white vertices.
Spider คือ tree ที่มีโหนดที่มีดีกรีมากกว่าสองไม่เกิน 1 จุดยอด ถ้ามี vertex ดังกล่าว จะเรียกว่าเป็น head ถ้าไม่มี spider จะเป็น path และจะสามารถเรียกโหนดใดเป็น head ก็ได้; เรียกจุดยอดที่ไม่ใช่ leaf และ head ว่า intermediate vertex, เรียก leaf ว่า foot, เรียก path จาก head ไป leaf ว่า leg
Decomposition
ChK แสดงว่า ให้กราฟ G ที่ทุก ๆ คู่ของจุดยอดสีดำ k-element connected, มีสับกราฟ H ของ G ที่สามารถ partition เป็น spiders ที่
- ทุก ๆ leaf เป็น black vertex
- ทุก ๆ black vertex เป็น leg ของ k spiders พอดี
- ทุก ๆ intermediate vertex เป็น white vertex (สังเกตว่า head เป็น black vertex ได้)
ด้านล่างแสดงตัวอย่างของ spiders