ผลต่างระหว่างรุ่นของ "204512-53/lecture2"
ไปยังการนำทาง
ไปยังการค้นหา
Wanchat111 (คุย | มีส่วนร่วม) |
Wanchat111 (คุย | มีส่วนร่วม) |
||
| แถว 2: | แถว 2: | ||
* การเรียงข้อมูล | * การเรียงข้อมูล | ||
| + | #Insertion Sort | ||
| + | #Bubble Sort | ||
=BIG O= | =BIG O= | ||
รุ่นแก้ไขเมื่อ 04:41, 8 กรกฎาคม 2553
เนื้อหา
Loop Invariants
- การเรียงข้อมูล
- Insertion Sort
- Bubble Sort
BIG O
Definition
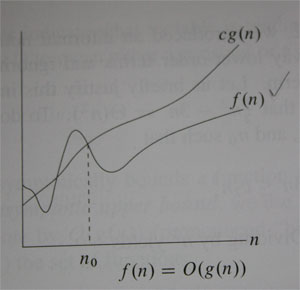
function f(n) เป็น O(g(n)) หรือ f(n) = O(g(n))
ถ้ามี n0 และ c(คือค่าคงที่) ที่
f(n) c.g(n) โดยที่ n n0
ตัวอย่าง กราฟ Big O
ตัวอย่าง1
พิสูจน์ 1000n = O(n2)
ถ้า n > 1000 n2 1000n
ให้ n0 = 1001 , c = 1 1000n 1n2
เมื่อ n 1001
Binary Search Tree
Red-Black Trees
- เป็น Binary tree
- Assume ว่าทุก node จบลงที่ Nil Node(All leaf node is Nil)
เงื่อนไข
- Node ใดๆจะเป็นสีแดงไม่ก็ดำ
- Root เป็นสีดำ
- Leaf เป็นสีดำ
- Node ใดเป็น Red Node Child ของ Node นั้นจะต้องเป็น Black Node
- จาก Node u ใดๆทุกๆ Path จาก Node ดังกล่าวไปยัง Leaf ของมันจะต้องมี Node ที่เป็นสีดำเท่ากันทั้งหมด
Lemma
Red-Black tree ที่มี n internal nodes จะมีความสูงไม่เกิน 2log(n+1)
Proof
นิยาม ที่ Node u ใดๆ bh(u) (black height ของ u) จะเท่ากับจำนวน Black Node จาก u ไป Node Leaf ใดๆ(ไม่นับ u))
Claim
สำหรับ internal node u ใดๆจำนวน internal node ใน sub-tree ใดๆที่ u เป็น rootจะมีค่าไม่น้อยกว่า 2^bh(u) -1
Proof (By induction)
ให้ w = u.left และ h = u.right
bh(w) ≥ bh(u) – 1
bh(x) ≥ bh(u) – 1
โดย Induction
Sub-tree ของ w มี internal node ≥ 2^bh(w) -1 ≥ 2^(bh(u)-1) -1
Sub-tree ของ x มี internal node ≥ 2^bh(x) -1 ≥ 2^(bh(u)-1) -1
ดังนั้น internal node ของ u = 1 + 2^(bh(u)-1) -1 + 2^(bh(u)-1) -1 = 2^bh(u) -1
พิจารณา Red-Black Tree ใดๆสูง h
bh(h) ≥ h/2 (เนื่องจาก Red Node จะต้องตามด้วย Black Node เสมอ)
จะได้ Internal node (n)
n ≥ 2^bh(h) -1
n ≥ 2^(h/2)-1
n+1 ≥ 2^(h/2)
log(n+1) ≤ h/2
h ≤2log(n+1)