ผลต่างระหว่างรุ่นของ "204512/บรรยาย 9"
Pattarika (คุย | มีส่วนร่วม) |
Pattarika (คุย | มีส่วนร่วม) |
||
| แถว 1: | แถว 1: | ||
| − | Dynamic Programming | + | [[Dynamic Programming]] |
| − | + | [[ภาพ:DP1.jpg]] | |
สมมุติต้องการเดินทางจากบ้าน ดช. ก ไปบ้าน ดญ. ข ระหว่างบ้าน ดช. ก กะ ดญ. ข ก็มีถนนตัดกันไปเรื่อยๆ | สมมุติต้องการเดินทางจากบ้าน ดช. ก ไปบ้าน ดญ. ข ระหว่างบ้าน ดช. ก กะ ดญ. ข ก็มีถนนตัดกันไปเรื่อยๆ | ||
คำถามคือ จากบ้าน ดช. ก ไปยังบ้าน ดญ.ข สามารถเดินทางโดยใช้เส้นทางต่างกันได้กี่แบบ | คำถามคือ จากบ้าน ดช. ก ไปยังบ้าน ดญ.ข สามารถเดินทางโดยใช้เส้นทางต่างกันได้กี่แบบ | ||
| − | + | <math>\begin{pmatrix} | |
| − | + | n+m \\ | |
| + | m | ||
| + | \end{pmatrix}</math> หรือ | ||
| + | <math>\begin{pmatrix} | ||
| + | n+m \\ | ||
| + | n | ||
| + | \end{pmatrix}</math> | ||
C(m,n) = C(m-1, n) + C(m,n-1) | C(m,n) = C(m-1, n) + C(m,n-1) | ||
C(0,0) เลือกได้ 1 วิธี | C(0,0) เลือกได้ 1 วิธี | ||
| แถว 11: | แถว 17: | ||
ในกรณีที่มีการ block เส้นทาง เราอาจจะเขียน pseudo code ได้ ให้ recursive ไปที่จุดที่ col-1, row-1 ไปเรื่อยๆ | ในกรณีที่มีการ block เส้นทาง เราอาจจะเขียน pseudo code ได้ ให้ recursive ไปที่จุดที่ col-1, row-1 ไปเรื่อยๆ | ||
| − | + | [[ภาพ:DP2.jpg]] | |
วิธีหนึ่งที่ใช้หาเส้นทาง | วิธีหนึ่งที่ใช้หาเส้นทาง | ||
| แถว 18: | แถว 24: | ||
Dynamic programming คือการคำนวนมาก่อนเพื่อหาผลเฉลย | Dynamic programming คือการคำนวนมาก่อนเพื่อหาผลเฉลย | ||
| − | Example | + | [[Example]] |
Function revolenchy | Function revolenchy | ||
F(0) = F(1) = 1 | F(0) = F(1) = 1 | ||
| แถว 29: | แถว 35: | ||
Return F[n] | Return F[n] | ||
นั่นคือ ถ้าอยากรู้ f(i) ต้องรู้ f(i-1), f(i-2) | นั่นคือ ถ้าอยากรู้ f(i) ต้องรู้ f(i-1), f(i-2) | ||
| + | [[ภาพ:DP3.jpg]] | ||
| + | ---- | ||
| + | |||
| + | [[Shortest path บน DAG (Directed Acyclic Graph)]] | ||
| − | |||
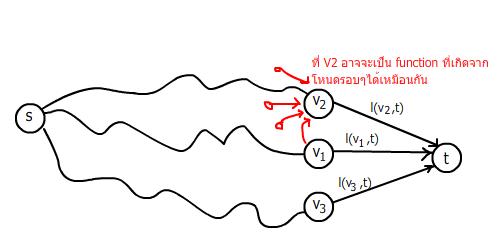
เราหา shortest path อย่างไร จาก st | เราหา shortest path อย่างไร จาก st | ||
t อาจมีตัวติดกันมากมาย shortest path ที่มาจาก ts ได้ | t อาจมีตัวติดกันมากมาย shortest path ที่มาจาก ts ได้ | ||
| แถว 37: | แถว 46: | ||
ถ้ามองแบบ recursive เราจะค่อยคลี่ออกแล้วมองปัญหาย่อยๆ | ถ้ามองแบบ recursive เราจะค่อยคลี่ออกแล้วมองปัญหาย่อยๆ | ||
| − | + | [[ภาพ:DP4.jpg]] | |
| + | <math>f(n) = min | ||
| + | \begin{cases} | ||
| + | D(v1) + l(v1,t) \\ | ||
| + | D(v2) + l(v2,t) \\ | ||
| + | D(v3) + l(v3,t) | ||
| + | \end{cases}</math> | ||
| − | |||
| − | |||
| − | |||
| − | |||
เราสามารถหาโดยไม่ต้องทำ recursive ก็ได้ โดยเรา evaluate ไปในทิศทางที่ขึ้นต่อกันเรื่อยๆ evaluate ด้วยลำดับที่เราเรียกว่า tropical order | เราสามารถหาโดยไม่ต้องทำ recursive ก็ได้ โดยเรา evaluate ไปในทิศทางที่ขึ้นต่อกันเรื่อยๆ evaluate ด้วยลำดับที่เราเรียกว่า tropical order | ||
ถ้าเรียงลำดับตาม tolopical order (คือเป็น order ที่ edge ชี้จากโหนดน้อยมาก) | ถ้าเรียงลำดับตาม tolopical order (คือเป็น order ที่ edge ชี้จากโหนดน้อยมาก) | ||
| − | S = | + | S = <math>v_0</math>, <math>v_1</math>, <math>v_2</math>, <math>v_3</math>, … , <math>v_n</math> |
Foreach vi, D(v1) infinity | Foreach vi, D(v1) infinity | ||
| แถว 61: | แถว 72: | ||
| − | Example | + | [[Example]] |
| + | |||
ถ้าเรามีเหรียญ 3, 5 บาท เราจะประกอบเหรียญให้เป็นเงินจำนวนไม่เกิน 100 บาท ได้กี่วิธี (ใช้เหรียญกี่เหรียญก็ได้) | ถ้าเรามีเหรียญ 3, 5 บาท เราจะประกอบเหรียญให้เป็นเงินจำนวนไม่เกิน 100 บาท ได้กี่วิธี (ใช้เหรียญกี่เหรียญก็ได้) | ||
| แถว 69: | แถว 81: | ||
ซึ่งอาจจะให้ผลดีขึ้นถ้าเราเก็บด้วยว่าเราใช้เหรียญไปกี่เหรียญ | ซึ่งอาจจะให้ผลดีขึ้นถ้าเราเก็บด้วยว่าเราใช้เหรียญไปกี่เหรียญ | ||
| − | Example | + | [[Example]] |
P(i) แทนจำนวนเหรียญที่เราใช้แล้วรวมกันได้ i บาท | P(i) แทนจำนวนเหรียญที่เราใช้แล้วรวมกันได้ i บาท | ||
| แถว 80: | แถว 92: | ||
| − | Example | + | [[Example]] |
มีถุงความจุเป็น L หน่วย | มีถุงความจุเป็น L หน่วย | ||
รุ่นแก้ไขเมื่อ 04:11, 15 สิงหาคม 2550
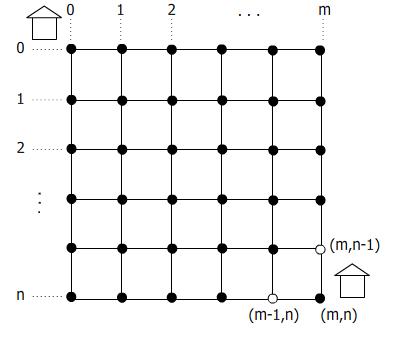 สมมุติต้องการเดินทางจากบ้าน ดช. ก ไปบ้าน ดญ. ข ระหว่างบ้าน ดช. ก กะ ดญ. ข ก็มีถนนตัดกันไปเรื่อยๆ
คำถามคือ จากบ้าน ดช. ก ไปยังบ้าน ดญ.ข สามารถเดินทางโดยใช้เส้นทางต่างกันได้กี่แบบ
หรือ
C(m,n) = C(m-1, n) + C(m,n-1)
C(0,0) เลือกได้ 1 วิธี
C(x,y) = 0 ถ้า x<0 หรือ y<0
สมมุติต้องการเดินทางจากบ้าน ดช. ก ไปบ้าน ดญ. ข ระหว่างบ้าน ดช. ก กะ ดญ. ข ก็มีถนนตัดกันไปเรื่อยๆ
คำถามคือ จากบ้าน ดช. ก ไปยังบ้าน ดญ.ข สามารถเดินทางโดยใช้เส้นทางต่างกันได้กี่แบบ
หรือ
C(m,n) = C(m-1, n) + C(m,n-1)
C(0,0) เลือกได้ 1 วิธี
C(x,y) = 0 ถ้า x<0 หรือ y<0
ในกรณีที่มีการ block เส้นทาง เราอาจจะเขียน pseudo code ได้ ให้ recursive ไปที่จุดที่ col-1, row-1 ไปเรื่อยๆ
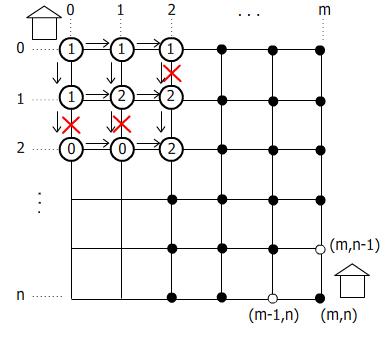 วิธีหนึ่งที่ใช้หาเส้นทาง
วิธีหนึ่งที่ใช้หาเส้นทาง
วิธีนี้เราจะทำการมองไปที่ทุกจุด จะใช้เวลา O(mn)
Dynamic programming คือการคำนวนมาก่อนเพื่อหาผลเฉลย
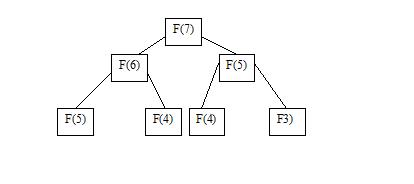
Example Function revolenchy F(0) = F(1) = 1 F(1) = F(i-1) + F(i-2) เมื่อ i>1
สังเกตว่ามันมีกรณีซ้ำซ้อนเกิดขึ้น
F[0]F[1]1
For i=2 to n do
F[i]F[i-1] + F[i-2]
Return F[n]
นั่นคือ ถ้าอยากรู้ f(i) ต้องรู้ f(i-1), f(i-2)
Shortest path บน DAG (Directed Acyclic Graph)
เราหา shortest path อย่างไร จาก st t อาจมีตัวติดกันมากมาย shortest path ที่มาจาก ts ได้ ถ้ามีนผ่าน v1, v2, v3 พวกนี้ต้องเป็น shortest path ด้วยเช่นเดียวกัน
ถ้ามองแบบ recursive เราจะค่อยคลี่ออกแล้วมองปัญหาย่อยๆ
เราสามารถหาโดยไม่ต้องทำ recursive ก็ได้ โดยเรา evaluate ไปในทิศทางที่ขึ้นต่อกันเรื่อยๆ evaluate ด้วยลำดับที่เราเรียกว่า tropical order
ถ้าเรียงลำดับตาม tolopical order (คือเป็น order ที่ edge ชี้จากโหนดน้อยมาก)
S = , , , , … ,
Foreach vi, D(v1) infinity D(v0) 0 For I = 1,…,n: D(vi) = min [D(Vj) + l(vj,vi)]
Vj: (Vj, Vi) E E
ขั้นตอนการแก้ปัญหา dynamic programming 1. เขียน recurrence (เริ่มต้นนิยามปัญหาย่อย) 2. หาลำดับเพื่อ evaluate 3. เขียน pseudo code
ถ้าเรามีเหรียญ 3, 5 บาท เราจะประกอบเหรียญให้เป็นเงินจำนวนไม่เกิน 100 บาท ได้กี่วิธี (ใช้เหรียญกี่เหรียญก็ได้)
เราอาจจะ plot เป็นตารางดังนี้
ตารางนี้เราทำการเก็บว่า ค่าไหนที่เกิดจากผลรวมของตัวมันบ้าง ซึ่งอาจจะให้ผลดีขึ้นถ้าเราเก็บด้วยว่าเราใช้เหรียญไปกี่เหรียญ
Example P(i) แทนจำนวนเหรียญที่เราใช้แล้วรวมกันได้ i บาท
P(i) = min P(i-1) + 1
P(i-3) + 1 if i-3 >= 0
P(i-4) + 1 i-4 >= 0
ตัวอย่างนี้เราสามารถหาเหรียญที่ใช้น้อยที่สุดได้ ถ้าถามต่ออีกว่า เราจะรู้ได้หรือไม่ ว่าใช้เหรียญอะไรไปบ้าง? วิธีการคือ เราจะเก็บ pointer ไว้ เพื่อดูว่าค่าผลรวมได้มาจากการรวมเหรียญไหนไปบ้าง
มีถุงความจุเป็น L หน่วย มีสินค้า k ประเภท ประเภทที่ i, มีน้ำหนัก wi หน่วย มีมูลค่า vi หน่วย
ให้หาสินค้าใส่ถุงโดย 1. ความจุรวม = L 2. มูลค่ารวมมากที่สุด
เลือกสินค้าที่ i มา 1 ชิ้น จะได้ว่า 1. P(i) = max P(i-wj) + Vj j:wj <= i 2. คำตอบคือ max P(i)
i: i <= L
A(i) = arg min P(i-wj) + Vj อัลกอริทึมนี้ จะรันอยู่ในเวลา O(kL) คำตอบนี้สำหรับปัญหาที่มี จำนวนสินค้าได้ไม่อั้น แต่สำหรับสินค้าที่มี จำนวนกัด เราจะแก้ไขปัญหาได้อย่างไร ปัญหาลักษณะนี้เราเรียกว่า Knapsack problem