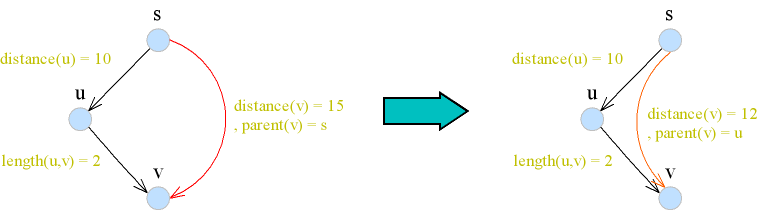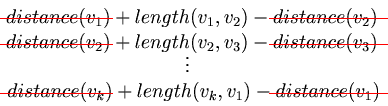ผลต่างระหว่างรุ่นของ "204512/บรรยาย 6"
Chalet16 (คุย | มีส่วนร่วม) (แก้ข้อความอ่านไม่ออก(ใช้ wget + KHexedit + HTML Decode) ยังแก้ได้แค่บางส่วน) |
Chalet16 (คุย | มีส่วนร่วม) (แก้ข้อความอ่านไม่ออก(ใช้ wget + KHexedit + HTML Decode) ทั้งหมด) |
||
| แถว 46: | แถว 46: | ||
lirelrol | lirelrol | ||
==Single Source Shortest Path== | ==Single Source Shortest Path== | ||
| − | + | ในปัญหา single source shortest path เราจะได้รับ source ''s'' แล้วหา shortest path จาก ''s'' ไปยังทุกๆ โหนด | |
| − | {{ | + | {{กล่องนิยาม| |
| − | ; | + | ;นิยาม : ต้นไม้ ''T'' ที่มี ''s'' เป็น root เป็น '''shortest path tree''' ถ้าทุกๆ path ใน ''T'' เป็น shortest path}} |
| − | + | ให้ต้นไม้ ''T'', เราให้ ''dist<sub>T</sub>'' แทนความยาวของ path ใน ''T'' จาก ''s'' ไป ''u'' ทฤษฎีบทด้านล่างให้เงื่อนไขที่รับรองว่า ''T'' เป็น shortest path tree | |
| − | {{ | + | {{กล่องทฤษฎีบท| |
'''Theorem:''' | '''Theorem:''' | ||
| − | + | ถ้าสำหรับทุก ๆ เส้นเชื่อม (''u'',''v'') ในกราฟ | |
<center><math>dist_T(v)\le dist_T(u) + length(u,v)</math></center> | <center><math>dist_T(v)\le dist_T(u) + length(u,v)</math></center> | ||
| − | + | แล้ว T จะเป็น shortest path tree | |
}} | }} | ||
| − | {{ | + | {{เริ่มบทพิสูจน์}} |
'''Proof'''<br> | '''Proof'''<br> | ||
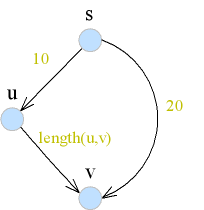
| − | [[ | + | [[ภาพ:sp03.png|thumb|right|ถ้า ''T'' เป็น shortest path tree |
| − | + | แล้ว length(u,v) <= 10]] | |
| − | : | + | :พิจารณา s-t path ใดๆ<br> |
| − | [[ | + | [[ภาพ:sp04.png]]<br> |
| − | :P | + | :P ยาว length(p)<br> |
| − | :path on tree | + | :path on tree ยาว dist <sub>T</sub>(t)<br> |
| − | :P | + | :P ต้องมีความยาวไม่น้อยกว่า path on tree ซึ่งเป็น shortest path ทำให้ T จะเป็น shortest path tree<br><br> |
| − | :Proof | + | :Proof ด้วยวิธี induction บน P<br> |
| − | :: | + | ::ให้ <math>P = <v_0,v_1,...,v_k>\,</math><br> |
| − | :: | + | ::ซึ่ง <math>v_0\,</math>=s , <math>v_k\,</math>=t<br> |
| − | :: | + | ::ดังนั้น <math>length(P) = length(v_0,v_1)+length(v_1,v_2)+...+length(v_k-1,v_k)\,</math><br> |
| − | :: | + | ::จาก <math>dist_T(v)\le dist_T(u) + length(u,v)</math> <br> |
| − | :: | + | ::เราทราบว่า<math>length(u,v) \ge dist_T(v) - dist_T(u)</math> <br> |
| − | :: | + | ::นำมา map กับ P<br> |
| − | :: | + | ::จะได้ว่า <math>length(P) \ge (dist_T(v_1)-dist_T(v_0))+(dist_T(v_2)-dist_T(v1))+...+(dist_T(v_k)-dist_T(v_k-1))</math> <br> |
::<math>length(P) \ge dist_T(v_k)-dist_T(v_0)</math><br> | ::<math>length(P) \ge dist_T(v_k)-dist_T(v_0)</math><br> | ||
::<math>length(P) \ge dist_T(t)-0</math><br> | ::<math>length(P) \ge dist_T(t)-0</math><br> | ||
| − | ::P | + | ::P มีความยาวไมน้อยกว่า path on tree ถ้าเงื่อนไขนี้เป็นตริง T จะเป็น shortest path tree<br> |
| − | {{ | + | {{จบบทพิสูจน์}} |
'''Algorithm''' | '''Algorithm''' | ||
| − | : | + | :เริ่มต้น |
:*<math>distance(u)\leftarrow \infty </math> for all <math>u \in V</math><br> | :*<math>distance(u)\leftarrow \infty </math> for all <math>u \in V</math><br> | ||
:*<math>distance(s)\leftarrow 0</math><br> | :*<math>distance(s)\leftarrow 0</math><br> | ||
:*parent(u)= null for all u<br> | :*parent(u)= null for all u<br> | ||
| − | : | + | :จากนั้นจึงทำ labelling step<br> |
==== Labelling Step ==== | ==== Labelling Step ==== | ||
| − | :: | + | ::เลือก edge(u,v) ที่ <math>distance(v)> distance(u) + length(u,v)\,</math> มา |
| − | :: | + | ::แล้วปรับค่า <math>distance(v)\leftarrow distance(u) + length(u,v)</math> |
| − | :: | + | ::และ <math>p(v)\leftarrow u</math><br> |
| − | [[ | + | [[ภาพ:sp05.png]] |
---- | ---- | ||
| − | {{ | + | {{กล่องทฤษฎีบท| |
'''Lemma''' | '''Lemma''' | ||
| − | : | + | :ถ้า <math>distance(u)\ne\infty</math> , จะมี path จาก s ไป u ที่มีความยาว distance(u)<br> |
}} | }} | ||
| − | {{ | + | {{เริ่มบทพิสูจน์}} |
'''Proof''' | '''Proof''' | ||
| − | : assume | + | : assume ว่า lemma จริงเมื่อตอนต้นการทำงาน<br> |
| − | : Proof by induction | + | : Proof by induction บนจำนวนของการทำ labelling step |
| − | ::assume | + | ::assume ว่า lemma จริงก่อนการทำงานของ step ใดๆ<br> |
| − | [[ | + | [[ภาพ:sp06.png]] |
| − | :: | + | ::เนื่องจาก <math>distance(u)\ne\infty</math> มี path p จาก s ไป u ที่มีความยาว distance(u) (by induction step)<br> |
| − | :: | + | ::หลังการทำงานตาม labelling step<br> |
::<math>distance(v)\leftarrow distance(u) + length(u,v)</math><br> | ::<math>distance(v)\leftarrow distance(u) + length(u,v)</math><br> | ||
| − | :: | + | ::ซึ่งเท่ากับความยาวของ <math>p' = p \cup \{u,v\}</math> |
| − | {{ | + | {{จบบทพิสูจน์}} |
---- | ---- | ||
| − | {{ | + | {{กล่องทฤษฎีบท| |
'''Lemma''' | '''Lemma''' | ||
| − | : | + | :ถ้า labelling step terminate ,parent p จะ form ตัวเป็น shortest path tree T |
| − | : | + | :และสำหรับ u ที่ <math>distance(u)\ne\infty</math> , distance(u)จะเท่ากับความยาวของ path ใน T จาก s ไป u |
}} | }} | ||
| − | ''' | + | '''กำหนดให้''' |
*<math>p^k(u) = p(p^{k-1}(u))\,</math> | *<math>p^k(u) = p(p^{k-1}(u))\,</math> | ||
*<math>p^1(u) = p(u)\,</math> | *<math>p^1(u) = p(u)\,</math> | ||
| − | {{ | + | {{เริ่มบทพิสูจน์}} |
'''Proof'''<br> | '''Proof'''<br> | ||
'''(I)''' | '''(I)''' | ||
| − | : | + | :ถ้า G มี negative cycle ที่ไปถึงได้จาก s, labelling step จะไม่หยุดการทำงาน<br><br> |
| − | : | + | :ไม่ว่า distance fucntion บนโหนดจะเป็น อย่างไร<br> |
| − | : | + | :จะมีบาง edge ที่ทำ labelling step ได้<br> |
| − | [[ | + | [[ภาพ:sp08.png]]<br> |
| − | : | + | :พิจารณา<br> |
:<math>distance(v)> distance(u) + length(u,v)\,</math><br> | :<math>distance(v)> distance(u) + length(u,v)\,</math><br> | ||
| − | : | + | :แสดงว่าจะมีการทำ labelling step เมื่อ <math>distance(u) + length(u,v) - distance(v) < 0\,</math><br> |
| − | : | + | :จากรูป มีโหนดจำนวน k โหนด เขียนออกมาได้ว่า<br><br> |
:<math>distance(v_1) + length(v_1,v_2) - distance(v_2)\,</math><br> | :<math>distance(v_1) + length(v_1,v_2) - distance(v_2)\,</math><br> | ||
:<math>distance(v_2) + length(v_2,v_3) - distance(v_3)\,</math><br> | :<math>distance(v_2) + length(v_2,v_3) - distance(v_3)\,</math><br> | ||
::::::::<math>\vdots</math><br> | ::::::::<math>\vdots</math><br> | ||
:<math>distance(v_k) + length(v_k,v_1) - distance(v_1)\,</math><br><br> | :<math>distance(v_k) + length(v_k,v_1) - distance(v_1)\,</math><br><br> | ||
| − | : | + | :ซึ่งจะสามารถทำ labelling step ได้ถ้าบางแถวยังมีค่าน้อยกว่า 0<br> |
| − | : | + | :เมื่อลองจับทุกแถวบวกกัน<br> |
| − | :[[ | + | :[[ภาพ:sp09.png]]<br><br> |
| − | : | + | :จะพบว่าเหลือแต่ค่า length รวมกันซึ่งก็คือ ความยาวของ path ใน cycle<br> |
| − | : | + | :ซึ่งถ้าเป็น negative cycle แสดงว่าต้องมีตัวใดตัวหนึ่งมีค่าติดลบ |
| − | : | + | :ทำให้สามารถทำ labelling step ได้เสมอ<br> |
'''(II)''' | '''(II)''' | ||
| − | : | + | :ไม่มี v ที่ <math>p^k(v)=v\,</math> สำหรับบางค่าของ k<br> |
| − | [[ | + | [[ภาพ:sp07.png]]<br> |
| − | : | + | :แต่เราปรับค่า d(u) นั่นคือ |
:<math>d(u) > d(u) + \sum_{i=1}^{k-1} length(e_i)</math><br> | :<math>d(u) > d(u) + \sum_{i=1}^{k-1} length(e_i)</math><br> | ||
:<math>d(u) > d(u) + length(c)\,</math><br> | :<math>d(u) > d(u) + length(c)\,</math><br> | ||
| − | : | + | :นั่นคือ <math>length(c) < 0\,</math><br><br> |
| − | : * | + | : *จากเบอร์ 1 กราฟไม่มี negative cycle<br> |
'''(III)''' | '''(III)''' | ||
| − | : | + | :ถ้ามี path จาก s ไป v<br> |
| − | :<math>dist(v)\ne \infty</math> | + | :<math>dist(v)\ne \infty</math> และ <math>p(v)\ne null</math> |
| − | : | + | :เพราะถ้ามี path ถึง v แสดงว่าต้องมีการ update มาถึง v เลยทำให้ <math>dist(v)\ne \infty</math> และ <math>p(v)\ne null</math> ด้วย<br><br> |
| − | + | จาก '''(I),(II),(III)''' จะสามารถ proof ได้กว่า <br> | |
| − | # parent | + | # parent จะ form ตัวกันเป็น tree T |
| − | # | + | # ทุกๆ edge ที่สอดคล้องกับ (I) ทำให้ T เป็น shortest path tree<br><br> |
| − | {{ | + | {{จบบทพิสูจน์}} |
== Labelling & Scanning Method == | == Labelling & Scanning Method == | ||
รุ่นแก้ไขปัจจุบันเมื่อ 13:33, 18 มีนาคม 2551
ertalia
บันทึกคำบรรยายวิชา 204512 นี้ เป็นบันทึกที่นิสิตเขียนขึ้น เนื้อหาโดยมากยังไม่ผ่านการตรวจสอบอย่างละเอียด การนำไปใช้ควรระมัดระวัง
จดบันทึกคำบรรยายโดย:
ณัฐ เรืองฤทธิ์ 50653773
อมรเดช แจ่มสว่าง 50653963
ในบทนี้จะพูดถึงปัญหาการหาเส้นทางที่สั้นที่สุด โดยจะเริ่มจากนิยามและพิสูจน์การมีอยู่ของเส้นทางที่สั้นที่สุดเมื่อไม่มีวงรอบที่เป็นลบ จากนั้นจะอธิบายถึง Single Source Shortest Path
เนื้อหา
นิยาม
เราจะเริ่มต้นด้วยนิยามของเส้นทางสั้นที่สุด
ให้ directed graph G = (V,E) และฟังก์ชัน ที่ระบุความยาวบนเส้นเชื่อม กล่าวคือความยาวของเส้นเชื่อม (u,v) คือ length(u,v)
สำหรับเส้นทาง P ใด ๆ เราจะนิยามความยาว length(P) เป็น
เส้นทางที่สั้นที่สุด (shotest path) จาก s ไป t คือเส้นทาง P ที่เริ่มที่ s สิ้นสุดที่ t ที่มีความยาวน้อยที่สุด
วงรอบที่เป็นลบกับเส้นทางที่สั้นที่สุด
ปัญหาแรกที่เราสนใจก็คือ: เส้นทางที่สั้นที่สุดจะมีในทุก ๆ กราฟหรือไม่?
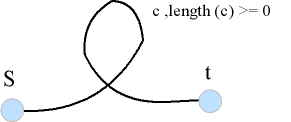
พิจารณากราฟต่อไปนี้
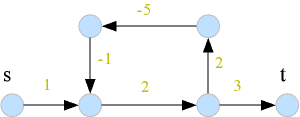
จากรูปจะเห็นได้ว่าถ้ามีการเลือกเส้นทางวนตรงกลางกราฟ จะสามารถวนซ้ำให้ค่าความยาวติดลบเท่าไหร่ก็ได้
เส้นทางดังกล่าวคือ negative length cycle
- นิยาม
- เราจะเรียกวงรอบที่มีความยาวเป็นลบ ว่า negative length cycle หรือ negative cycle
เราจะเรียก path ใด ๆ ว่าเป็น simple path ถ้าไม่มีโหนดใดๆ ประกฎใน path มากกว่า 1 ครั้ง และจะเรียก path ใด ๆ ว่าเป็น s-t path ถ้า path นั้นเริ่มที่ s และสิ้นสุดที่ t
ทฤษฎีบทด้านล่างแสดงว่าถ้ากราฟจะมีเส้นทางที่สั้นที่สุด เมื่อและต่อเมื่อ กราฟไม่มีวงรอบที่เป็นลบ
Theorem: ถ้าไม่มี negative cycle C ที่ไปถึงได้จาก s และบางใหนดใน C สามารถไปถึง t ได้, จะมี shortest path จาก s ไป t
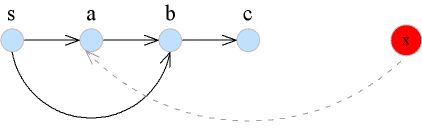
Proof: สังเกตว่าสำหรับ s-t path P ใดๆ จะมี simple s-t path P' ที่มีความยาวไม่มากกว่า P ทั้งนี้เนื่องจากถ้าเส้นทางนั้นมี cycle เราสามารถตัด cycle นั้นออกได้โดยไม่ทำให้ความยาวของเส้นทางที่ได้ยาวขึ้น (ดูรูปด้านล่าง)
เนื่องจากจำนวน simple s-t path มีจำกัด (ไม่เกิน n! path) เมื่อ n = จำนวนโหนดในกราฟ ดังนั้นจะมี path ที่มีความยาวสั้นที่สุด
lirelrol
Single Source Shortest Path
ในปัญหา single source shortest path เราจะได้รับ source s แล้วหา shortest path จาก s ไปยังทุกๆ โหนด
- นิยาม
- ต้นไม้ T ที่มี s เป็น root เป็น shortest path tree ถ้าทุกๆ path ใน T เป็น shortest path
ให้ต้นไม้ T, เราให้ distT แทนความยาวของ path ใน T จาก s ไป u ทฤษฎีบทด้านล่างให้เงื่อนไขที่รับรองว่า T เป็น shortest path tree
Theorem: ถ้าสำหรับทุก ๆ เส้นเชื่อม (u,v) ในกราฟ
แล้ว T จะเป็น shortest path tree
Proof
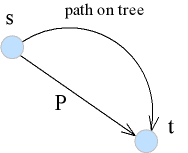
- พิจารณา s-t path ใดๆ
- P ยาว length(p)
- path on tree ยาว dist T(t)
- P ต้องมีความยาวไม่น้อยกว่า path on tree ซึ่งเป็น shortest path ทำให้ T จะเป็น shortest path tree
- Proof ด้วยวิธี induction บน P
- ให้
- ซึ่ง =s , =t
- ดังนั้น
- จาก
- เราทราบว่า
- นำมา map กับ P
- จะได้ว่า
- P มีความยาวไมน้อยกว่า path on tree ถ้าเงื่อนไขนี้เป็นตริง T จะเป็น shortest path tree
Algorithm
- เริ่มต้น
- for all
- parent(u)= null for all u
- for all
- จากนั้นจึงทำ labelling step
Labelling Step
- เลือก edge(u,v) ที่ มา
- แล้วปรับค่า
- และ
Lemma
- ถ้า , จะมี path จาก s ไป u ที่มีความยาว distance(u)
Proof
- assume ว่า lemma จริงเมื่อตอนต้นการทำงาน
- Proof by induction บนจำนวนของการทำ labelling step
- assume ว่า lemma จริงก่อนการทำงานของ step ใดๆ
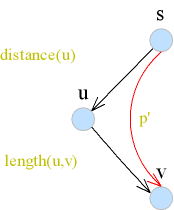
- เนื่องจาก มี path p จาก s ไป u ที่มีความยาว distance(u) (by induction step)
- หลังการทำงานตาม labelling step
- ซึ่งเท่ากับความยาวของ
Lemma
- ถ้า labelling step terminate ,parent p จะ form ตัวเป็น shortest path tree T
- และสำหรับ u ที่ , distance(u)จะเท่ากับความยาวของ path ใน T จาก s ไป u
กำหนดให้
Proof
(I)
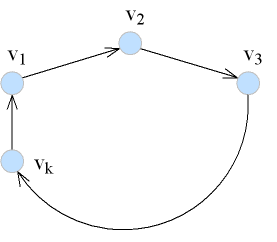
- ถ้า G มี negative cycle ที่ไปถึงได้จาก s, labelling step จะไม่หยุดการทำงาน
- ไม่ว่า distance fucntion บนโหนดจะเป็น อย่างไร
- จะมีบาง edge ที่ทำ labelling step ได้
- พิจารณา
- แสดงว่าจะมีการทำ labelling step เมื่อ
- จากรูป มีโหนดจำนวน k โหนด เขียนออกมาได้ว่า
- ซึ่งจะสามารถทำ labelling step ได้ถ้าบางแถวยังมีค่าน้อยกว่า 0
- เมื่อลองจับทุกแถวบวกกัน
- จะพบว่าเหลือแต่ค่า length รวมกันซึ่งก็คือ ความยาวของ path ใน cycle
- ซึ่งถ้าเป็น negative cycle แสดงว่าต้องมีตัวใดตัวหนึ่งมีค่าติดลบ
- ทำให้สามารถทำ labelling step ได้เสมอ
(II)
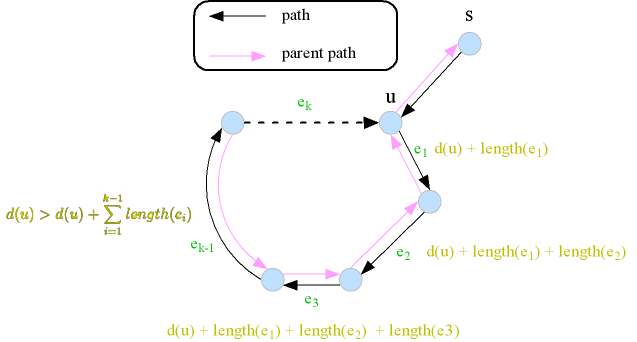
- ไม่มี v ที่ สำหรับบางค่าของ k
- แต่เราปรับค่า d(u) นั่นคือ
- นั่นคือ
- *จากเบอร์ 1 กราฟไม่มี negative cycle
(III)
- ถ้ามี path จาก s ไป v
- และ
- เพราะถ้ามี path ถึง v แสดงว่าต้องมีการ update มาถึง v เลยทำให้ และ ด้วย
จาก (I),(II),(III) จะสามารถ proof ได้กว่า
- parent จะ form ตัวกันเป็น tree T
- ทุกๆ edge ที่สอดคล้องกับ (I) ทำให้ T เป็น shortest path tree
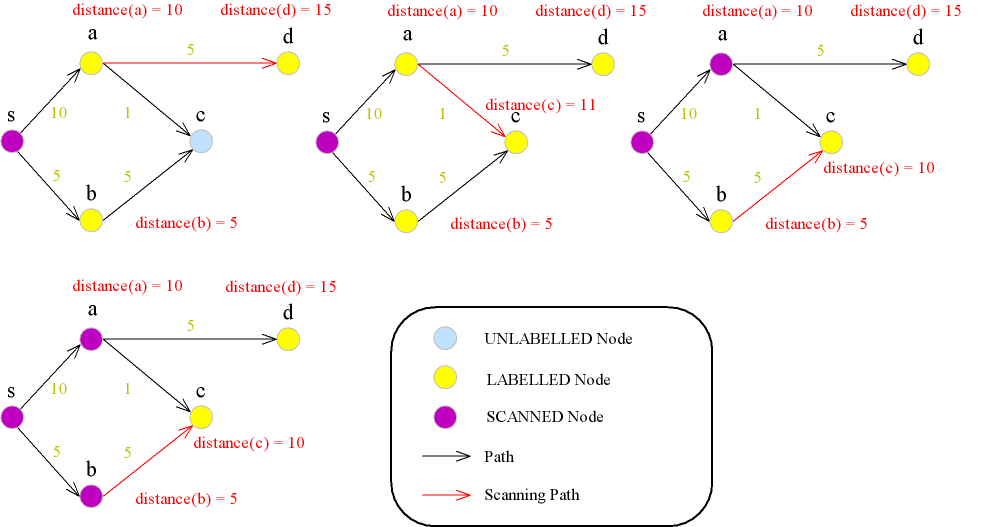
Labelling & Scanning Method
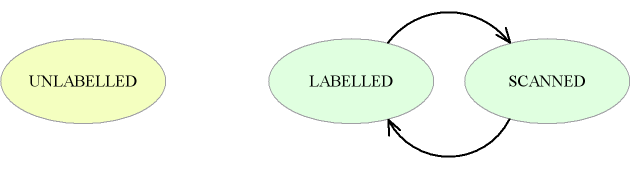
แต่ละโหนดจะมีสถานะได้ดังนี้
- Unlabelled
- Labelled
- Scanned
- เริ่มต้นโหนดทุกโหนดยกเว้น s จะมีสถานะเป็น Unlabelled และ s มีสถานะเป็น Labelled
- และทุกครั้งที่ distance(u) เปลี่ยน u จะมีสถานะเป็น Labelled
Pre-Condition u มีสถานะเป็น Labelled
- SCAN(u):
- if distance(v) > distance(u) + length(u,v)
- เปลี่ยนสถานะของ v เป็น Labelled
- if distance(v) > distance(u) + length(u,v)
- SCAN(u):
- Claim : ถ้าทำตามวิธี Labelling & Scanning Method แล้วไม่แหลือโหนดที่มีสถานะเป็น Labelled เลย เราจะไม่สามารถทำ Labelling Step ได้อีก
Efficient Scanning Order
- (I) กราฟที่ไม่มี cycle [Directed Acyclic Graph - DAG]
- คือกราฟที่ไม่มีการเรียงแบบ Topological ของโหนด
- Running time จาก Algorithm นี้คือ O(m+n)
- ***Topological ของโหนด คือ การเรียงของโหนดที่รับประกันได้ว่าไม่มี edge จากโหนดด้านหลังชี้มายังโหนดด้านหน้า
- (II) กราฟไม่มี edge ที่ความยาวเป็นลบ [Dijkstra's Algorithm]
- ในบรรดาโหนดที่มีสถานะเป็น Labelled ให้ Scan โหนด w ที่ distance(w) น้อยที่สุด โดยจะไม่ Scan ซ้ำ
- จะใช้ Priority Queue : เข้ามาช่วยในการทำ Algorithm โดยที่
| Enqueue(k,v) | เพิ่ม (k,v) ลงใน Set |
| FindMin | ที่มีค่า k น้อยที่สุด |
| ExtractMin | ที่มีค่า k น้อยที่สุดและลบ (k,v) ออกจาก S |
| Update((k,v),k') | Update k ด้วย k' |
- Dijkstra's Algorithm
- Running Time จะแบ่งเป็น 2 ช่วงได้แก่ช่วงของการ ExtractMin (O(n)) และช่วงของการ UpdateQueue (O(m)) ซึ่งจะแตกต่างกันไป
- ตามการจัดวางของ Graph แบบต่างๆ โดยสามารถเทียบเป็นตารางได้ดังนี้
| ExtractMin | UpdateQueue | Total | |
| Array ของโหนด (Dijkstra) |
O(n) | O(1) | O(n^2) |
| Binary Heap | O(logn) | O(logn) | O((m+n)logn) |
| Fibonacci Heap | O(logn) | decrease key O(1) amortized |
O(nlogn+m) |
- (III) กราฟทั่วไป [Bellman - Ford - Moore]
- เป็นการ Scan ทุกๆ โหนดเป็นจำนวน n-1 รอบ เพราะฉะนั้น Running Time จะเป็น O(nm)