ผลต่างระหว่างรุ่นของ "418531 ภาคต้น 2552/โจทย์ปัญหาอัลกอริทึมแบบตะกละ II/เฉลยข้อ 7"
Aoy (คุย | มีส่วนร่วม) |
|||
| แถว 1: | แถว 1: | ||
| − | สังเกตได้ว่า cycle ที่มีความยาวเป็น 4 นั้น ถ้าพิจารณาอีกมุมหนึ่งก็คือ vertex 4 vertex ที่มี edge เชื่อมจาก vertex ที่หนึ่งไป vertex ที่สอง จาก vertex ที่สองไป vertex ที่สาม จาก vertex ที่สามไป vertex ที่สี่ และจาก vertex | + | สังเกตได้ว่า cycle ที่มีความยาวเป็น 4 นั้น ถ้าพิจารณาอีกมุมหนึ่งก็คือ vertex 4 vertex ที่มี edge เชื่อมจาก vertex ที่หนึ่งไป vertex ที่สอง จาก vertex ที่สองไป vertex ที่สาม จาก vertex ที่สามไป vertex ที่สี่ และจาก vertex ที่สี่ไป vertex ที่หนึ่งนั่นเอง ดังนั้นถ้าเราใช้เทคนิคแบบ brute force เราจะได้ว่า วัตถุที่เราต้องการค้นหาคือ vertex 4 vertex จากทั้งหมด <math> n=|V| \,</math> vertex ที่มีเงื่อนไขข้างต้นนั่นเอง ดังนั้นเวลาการทำงานของอัลกอริทึมแบบ brute force นี้จะเป็น <math> {n \choose 4}=O(n^4) \,</math> นั่นเอง แต่เนื่องจากโจทย์ข้อนี้ต้องการให้ได้เวลาการทำงานเป็น <math> O(n^3) \,</math> ดังนั้น อัลกอริทึมข้างต้นจึงใช้ไม่ได้ |
เราจะใช้อัลกอริทึมต่อไปนี้แทน | เราจะใช้อัลกอริทึมต่อไปนี้แทน | ||
| แถว 7: | แถว 7: | ||
[[ไฟล์:greedy2_7.JPG]] | [[ไฟล์:greedy2_7.JPG]] | ||
| − | จาก cycle | + | จาก cycle ที่มีความยาวสี่ข้างต้น เราจะได้ว่า จากเดิมที่ต้องเลือก vertex 4 vertex มาแล้วหา edge เชื่อมระหว่าง vertex ทั้งสี่นี้ เราสามารถ เลือก vertex มาแค่ 2 vertex ซึ่งการเลือก vertex 2 vertex จาก n vertex จะได้เวลาการทำงานเป็น <math> O(n^2) \,</math> และโจทย์ต้องการให้ได้เวลาการทำงานทั้งหมดเป็น <math> O(n^3) \,</math> ดังนั้นถ้าเราสามารถหาอีก 2 vertex ที่เหลือได้ในเวลาการทำงานอีก <math> O(n) \,</math> เราก็จะได้เวลาการทำงานรวมเป็น <math> O(n^3) \,</math> ตามที่ต้องการ |
| − | จากตัวอย่าง โดยไม่เสียความเป็นทั่วไป สมมติให้เราเลือก vertex มาสอง vertex คือ <math> a \,</math> กับ <math> d \,</math> แล้วเราสามารถหา vertex ที่เหลือคือ <math> b \,</math> กับ <math> c \,</math> ได้ดังนี้ พิจารณา adjacency matirx ที่ใช้แทนกราฟนี้ พิจารณาว่า ถ้าเราจะหาอีกสอง vertex (<math> b,c \,</math>) ที่มี edge เชื่อมกับ สอง vertex ที่เราเลือกมาแล้ว (<math> a,d \,</math>) | + | จากตัวอย่าง โดยไม่เสียความเป็นทั่วไป สมมติให้เราเลือก vertex มาสอง vertex คือ <math> a \,</math> กับ <math> d \,</math> แล้วเราสามารถหา vertex ที่เหลือคือ <math> b \,</math> กับ <math> c \,</math> ได้ดังนี้ พิจารณา adjacency matirx ที่ใช้แทนกราฟนี้ พิจารณาว่า ถ้าเราจะหาอีกสอง vertex (<math> b,c \,</math>) ที่มี edge เชื่อมกับ สอง vertex ที่เราเลือกมาแล้ว (<math> a,d \,</math>)ได้โดยพิจารณา row ต่าง ๆ ใน matrix ถ้ามี row อย่างน้อย 2 row ที่มีเลข 1 ตรง column <math> a \,</math> กับ <math> d \,</math> พร้อมกัน เราก็จะเลือก vertex ที่อยู่ใน row นั้น(ถ้ามีมากกว่า 2 ให้เลือกสองตัวใด ๆ ก็ได้) ซึ่งการทำแบบจะใช้เวลาอย่างมาก คือสำรวจ row ทุก ๆ row ใน matrix ซึ่งจำนวน row ทั้งหมดจะเท่ากับจำนวน vertex ซึ่งก็คือ <math> n \,</math> นั่นเอง สรุปอัลกอริทึมคือ เลือก vertex 2 vertex จาก n vertex และสำหรับแต่ละคู่ของ vertex ที่เลือกมาข้างต้น เราก็ไล่หาไปตาม row ใน adjacency matrix หาอีกสอง row ที่มีเลข 1 ตรง column ของ vertex สอง vertex ที่เราเลือกข้างต้นตรงกัน เราจะได้ว่า อัลกอริทึมข้างต้นใช้เวลาในการเลือกสอง vertex แรกเป็น <math> O(n^2) \,</math> และสำหรับแต่ละคู่ของ vertex ที่เลือกใช้เวลาสำรวจ row อีก <math> O(n) \,</math> ดังนั้นเวลาการทำงานทั้งหมดจึงเป็น <math> O(n^3) \,</math> ตามต้องการ |
รุ่นแก้ไขปัจจุบันเมื่อ 08:58, 30 กันยายน 2552
สังเกตได้ว่า cycle ที่มีความยาวเป็น 4 นั้น ถ้าพิจารณาอีกมุมหนึ่งก็คือ vertex 4 vertex ที่มี edge เชื่อมจาก vertex ที่หนึ่งไป vertex ที่สอง จาก vertex ที่สองไป vertex ที่สาม จาก vertex ที่สามไป vertex ที่สี่ และจาก vertex ที่สี่ไป vertex ที่หนึ่งนั่นเอง ดังนั้นถ้าเราใช้เทคนิคแบบ brute force เราจะได้ว่า วัตถุที่เราต้องการค้นหาคือ vertex 4 vertex จากทั้งหมด vertex ที่มีเงื่อนไขข้างต้นนั่นเอง ดังนั้นเวลาการทำงานของอัลกอริทึมแบบ brute force นี้จะเป็น นั่นเอง แต่เนื่องจากโจทย์ข้อนี้ต้องการให้ได้เวลาการทำงานเป็น ดังนั้น อัลกอริทึมข้างต้นจึงใช้ไม่ได้
เราจะใช้อัลกอริทึมต่อไปนี้แทน
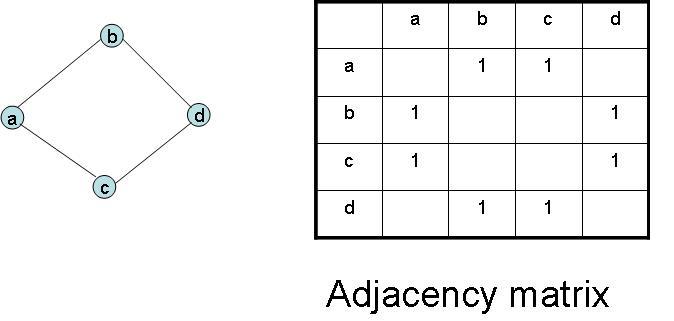
พิจารณา cycle ที่มีความยาวสี่ ต่อไปนี้
จาก cycle ที่มีความยาวสี่ข้างต้น เราจะได้ว่า จากเดิมที่ต้องเลือก vertex 4 vertex มาแล้วหา edge เชื่อมระหว่าง vertex ทั้งสี่นี้ เราสามารถ เลือก vertex มาแค่ 2 vertex ซึ่งการเลือก vertex 2 vertex จาก n vertex จะได้เวลาการทำงานเป็น และโจทย์ต้องการให้ได้เวลาการทำงานทั้งหมดเป็น ดังนั้นถ้าเราสามารถหาอีก 2 vertex ที่เหลือได้ในเวลาการทำงานอีก เราก็จะได้เวลาการทำงานรวมเป็น ตามที่ต้องการ
จากตัวอย่าง โดยไม่เสียความเป็นทั่วไป สมมติให้เราเลือก vertex มาสอง vertex คือ กับ แล้วเราสามารถหา vertex ที่เหลือคือ กับ ได้ดังนี้ พิจารณา adjacency matirx ที่ใช้แทนกราฟนี้ พิจารณาว่า ถ้าเราจะหาอีกสอง vertex () ที่มี edge เชื่อมกับ สอง vertex ที่เราเลือกมาแล้ว ()ได้โดยพิจารณา row ต่าง ๆ ใน matrix ถ้ามี row อย่างน้อย 2 row ที่มีเลข 1 ตรง column กับ พร้อมกัน เราก็จะเลือก vertex ที่อยู่ใน row นั้น(ถ้ามีมากกว่า 2 ให้เลือกสองตัวใด ๆ ก็ได้) ซึ่งการทำแบบจะใช้เวลาอย่างมาก คือสำรวจ row ทุก ๆ row ใน matrix ซึ่งจำนวน row ทั้งหมดจะเท่ากับจำนวน vertex ซึ่งก็คือ นั่นเอง สรุปอัลกอริทึมคือ เลือก vertex 2 vertex จาก n vertex และสำหรับแต่ละคู่ของ vertex ที่เลือกมาข้างต้น เราก็ไล่หาไปตาม row ใน adjacency matrix หาอีกสอง row ที่มีเลข 1 ตรง column ของ vertex สอง vertex ที่เราเลือกข้างต้นตรงกัน เราจะได้ว่า อัลกอริทึมข้างต้นใช้เวลาในการเลือกสอง vertex แรกเป็น และสำหรับแต่ละคู่ของ vertex ที่เลือกใช้เวลาสำรวจ row อีก ดังนั้นเวลาการทำงานทั้งหมดจึงเป็น ตามต้องการ