ผลต่างระหว่างรุ่นของ "204512-53/lecture3"
ไปยังการนำทาง
ไปยังการค้นหา
Meenkaza (คุย | มีส่วนร่วม) (หน้าที่ถูกสร้างด้วย '=Red-Black Tree (Cont.)= *Tree ใดๆ จะเป็น Red-Black Tree ได้ต้องมีคุณสมบัติ 5 ข…') |
Meenkaza (คุย | มีส่วนร่วม) |
||
| แถว 26: | แถว 26: | ||
[[ไฟล์:Merge_Sort_cr.png]] | [[ไฟล์:Merge_Sort_cr.png]] | ||
| + | |||
| + | ===Algorithm=== | ||
| + | เราจะได้อัลกอริทึมในการ Merge โดยให้ k=0, i=1, j=1 | ||
| + | |||
| + | 1. While k < n+m | ||
| + | 2. k <math>\Leftarrow</math> k+1 | ||
| + | 3. if A[i] < B[j] | ||
| + | 4. C[k] <math>\Leftarrow</math> A[i] | ||
| + | 5. i <math>\Leftarrow</math>i+1 | ||
| + | 6. else | ||
| + | 7. C[k] <math>\Leftarrow</math> B[j] | ||
| + | 8. j <math>\Leftarrow</math> j+1 | ||
| + | |||
| + | ===Proof=== | ||
| + | เราจะพิสูจน์ว่าอัลกอริทึมข้างบนถูกต้อง โดย | ||
| + | *ถ้า array A เรียงจากน้อยไปหามาก และ | ||
| + | *ถ้า array B เรียงจากน้อยไปหามาก แล้ว | ||
| + | *Array C จะเป็น array ที่มาจาก array A และ array B ที่เรียงจากน้อยไปหามาก | ||
รุ่นแก้ไขเมื่อ 10:57, 12 สิงหาคม 2553
เนื้อหา
Red-Black Tree (Cont.)
- Tree ใดๆ จะเป็น Red-Black Tree ได้ต้องมีคุณสมบัติ 5 ข้อ ได้แก่
- โหนดเป็นได้ 2 สี คือ แดง กับ ดำ
- Root ต้องเป็นสีดำ
- Leaf ทั้งหมดต้องเป็นสีดำ
- โหนดสีแดงมีโหนดลูกเป็นสีดำ ทั้ง 2 โหนด
- จากโหนดใดๆ ไปหา Leaf ที่เป็นลูกหลานของตัวเอง จะต้องมีจำนวนโหนดสีดำเท่ากันหมด
ความสูงของ Red-Black Tree เป็น O(log n)
วิธีแก้ปัญหา เมื่อเพิ่ม Leaf Node เข้าไปใหม่ที่จุดใดจุดหนึ่ง ใน Leaf Node ที่เพิ่มเข้าไปใหม่ เราต้องทำการปรับสมดุลใหม่ โดยการตรวจสอบแล้วเปลี่ยนสีในบางจุดที่ต้องเปลี่ยนให้ตรงกับคุณสมบัติของ Red-Black Tree ทั้ง 5 ข้อไปเรื่อยๆ ไล่ตั้งแต่ Leaf Node ที่ได้ทำการเพิ่มเข้ามาขึ้นไปจนถึง Root
Divide and Conqure
เป็นยุทธศาสตร์ในการแก้ปัญหาด้วยอัลกอริทึมแบบหนึ่ง เช่น ถ้าต้องการหาข้อมูลอันหนึ่ง ให้จิ้มไปที่จุดกึ่งกลาง ถ้าเจอคำตอบก็จบ แต่ถ้าไม่เจอ เราก็เลือกว่าควรจะไปทางมากกว่าหรือน้อยกว่า (เนื่องจาก Binary Search นั้น ข้อมูลได้มีการเรียงกันก่อนอยู่แล้ว)
Concept – ตีเมืองใหญ่ให้เป็นเมืองเล็กก่อน
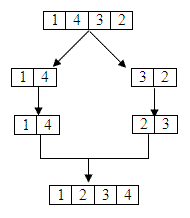
Review Merge Sort
- จิ้มไปที่กิ่งกลางจะได้ array 2 ส่วน คือ Array Aขนาด n และ Array B ขนาด m
- ซึ่ง array แต่ละส่วนจะทำการ Sort ใน Array ของตัวเอง เรียกว่า Merge Sort
- หลังจากนั้นทำการ เปรียบค่าแต่ละค่า ในแต่ละ Index ระหว่าง array ได้ค่าไหนที่น้อยกว่าก็ทำการ Add เข้าไปใน array ใหม่ ชื่อว่า C และทำไปเรื่อยๆ จนครบ เรียกว่า การ Merge
Algorithm
เราจะได้อัลกอริทึมในการ Merge โดยให้ k=0, i=1, j=1
1. While k < n+m 2. k k+1 3. if A[i] < B[j] 4. C[k] A[i] 5. i i+1 6. else 7. C[k] B[j] 8. j j+1
Proof
เราจะพิสูจน์ว่าอัลกอริทึมข้างบนถูกต้อง โดย *ถ้า array A เรียงจากน้อยไปหามาก และ *ถ้า array B เรียงจากน้อยไปหามาก แล้ว *Array C จะเป็น array ที่มาจาก array A และ array B ที่เรียงจากน้อยไปหามาก