204512/บรรยาย 3
เนื้อหา
ความรู้เบื้องต้น
Tree เป็นโครงสร้างชนิดไม่เชิงเส้น (Non-linear) มีลักษณะเป็น recursive ประกอบไปด้วยสมาชิกที่เรียกว่า Node และมีเส้นที่เชื่อมระหว่าง Node ที่เรียกว่า branch คำสำคัญที่เกี่ยวกับ Tree มีดังนี้
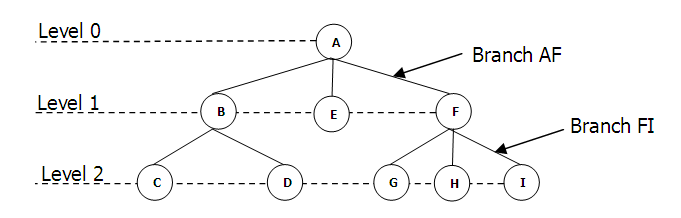
| Root Node: A | Sibling Node: {B, E, F}, {C, D}, {G, H, I} |
| Parents Node: A, B, F | Leaves Node: C, D, E, G, H, I |
| Child Node: B, E, F, C, D, G, H, I | Internal Node: B, F |
- Root Node คือ โหนดที่อยู่บนสุดของต้นไม้
- Leaf Node คือ โหนดที่ไม่มีลูกหรือโหนดอื่นต่อ เรียกอีกอย่างหนึ่งว่า External Node
- Internal Node คือ โหนดที่ไม่ใช่ Root และ Leaf Node
- Depth คือ ความยาวจาก Root node ถึง Node ที่สนใจ
- Height คือ ความยาวจาก Node ที่สนใจถึง Leaf Node ที่ลึกที่สุดที่มี Node ที่สนใจเป็น Parent
Binary Search Tree
Binary Search Tree คือ Data Structure ที่ define แบบ Recursive โดยขั้นตอนวิธีการทำงานที่สำคัญของ Binary Tree จะสนับสนุนการทำงานดังต่อไปนี้
- Find (key)
- Insert (key)
- Delete (key)
ซึ่งเวลาที่ใช้ในการค้นหานั้นจะขึ้นอยู่กับความสูงของต้นไม้ โดยถ้ามีข้อมูล n ตัวความสูงของต้นไม้จะไม่ลึกไปกว่า O(log n) ถ้าสูงกว่าจะทำให้เกิด Worse-case
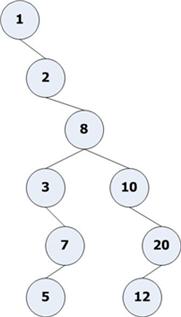
สมมติว่ามี data 1,2,8,3,7,5,10,20,12 เขียนเป็น Binary Search Tree ได้ดังนี้
AVL Tree
AVL (Adelson-Velskii and Landis) tree คือ binary search tree ที่มีเงื่อนไขของความสมดุล (Balance Condition) โดยเงื่อนไขดังกล่าวคือ
Condition: ในทุกๆ โหนด ความสูงของ subtree ทางด้ายซ้ายและด้านขวาต่างกันไม่เกิน 1 โดยที่ให้ N(k) แทนจำนวนโหนดที่น้อยที่สุดใน AVL Tree ที่มีความสูง k
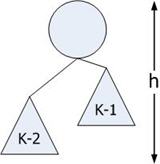
จากเงื่อนไขของ AVL Tree จะสรุปได้
N(1) = 1, N(2) = 2
N(k) = N(k-1) + N(k-2) + 1
จะสังเกตได้ว่ามีลักษณะเป็น Fibonacci แต่มีการบวก 1 เข้ามาด้วย
จากสมการข้างต้น
N(k) = N(k-1) + N(k-2) + 1
N(k) = N(k-2) + N(k-3) + N(k-2) + 1
≥ 2N(k-2)
≥
≥ ---*
จะสังเกตได้ว่าฟังก์ชันดังกล่าวมีขนาดเป็น Exponential ใน k
สรุป: AVL Tree ที่มี n โหนดจะมีความสูง O(log n)
การหมุนของ AVL Tree
การหมุน (Rotation) ของ AVL Tree กระทำเพื่อให้ต้นไม้ที่ไม่อยู่ในเงื่อนไขของ AVL Tree กลับเข้ามาอยู่ในเงื่อนไข ซึ่งมีรูปแบบการทำงานดังนี้
- Single Rotation
- การหมุนทางขวา (Right Rotation)
- การหมุนทางซ้าย (Left Rotation)
- Double Rotation
การหมุนทางขวา (Right Rotation)
จะกระทำเมื่อทางด้านซ้ายของต้นไม้มีความสุงกว่าด้านขวาเกิน 1 ซึ่งไม่ตรงตามเงื่อนไขของ AVL Tree จึงใช้การกระทำที่เรียกว่า “การหมุนทางขวา” เพื่อทำให้ตรงตามเงื่อนไขดังกล่าว

การหมุนทางซ้าย (Left Rotation)
ในทางกลับกันถ้าหากทางด้านขวาของต้นไม้มีความสูงไม่สัมพันธ์กับเงื่อนไขของ AVL Tree จะทำการหมุนทางซ้ายเพื่อให้ต้นไม้กลับมาสมดุล
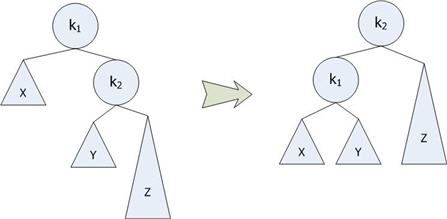
ตัวอย่าง Single Rotation โดยการใส่ตัวเลข 1 – 7 ตามลำดับ
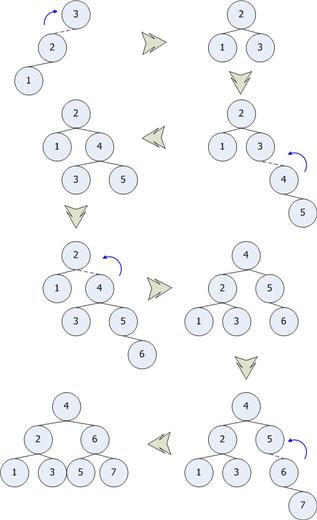
การ Double Rotation
ในบางครั้งการหมุนสามารถทำการหมุนได้หลาย ครั้งเช่น เมื่อทำการหมุนซ้ายแล้วทำการหมุนขวา หรือทำการหมุนขวาแล้วหมุนซ้าย โดยอาศัยเทคนิคการหมุนทางซ้ายและทางขวาร่วมกัน
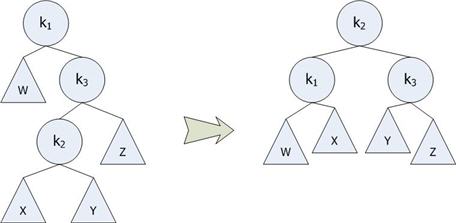
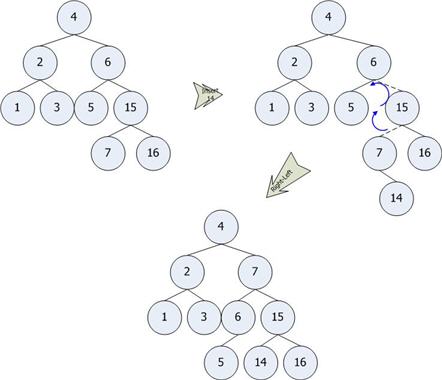
ตัวอย่าง Double Rotation โดยการใส่ตัวเลข 14 เข้าไปในต้นไม้
Amortized Analysis
เป็นการคิดการชาร์จเวลาการทำงานในการทำงานในส่วนกิจกรรมย่อยๆ เพื่อนำมาใช้ทดแทนกิจกรรมอื่นในภายหลัง ยกตัวอย่างเช่น การทำงานกับ Variable Array เมื่อ insert ข้อมูลเต็ม array แล้ว เราต้องทำการเพิ่ม array แล้วทำการคัดลอก array เก่า
สมมุติมี array 1 ชุดเมื่อมีการเต็มข้อมูลเต็มแล้วก็จะมีการจอง array ใหม่แล้วคัดลอกข้อมูลของเดิมมาเก็บที่ไหม่ ดังนั้นถ้ามีข้อมูล n ตัว จะต้องใช้เวลาถึง O(n2)
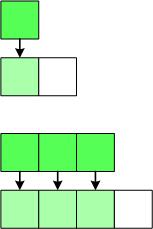
แต่เมื่อเราใช้การคิดเวลาแบบ Amortized แล้ว เราสามารถคิดแบบเวลาที่ทำทั้งหมด โดยใช้เวลาไม่เกินเท่าไร ซึ่งมีการคิดเวลาล่วงหน้าและมีการจองพื้นที่ array เป็นสองเท่าจากข้อมูลที่มีอยู่
ซึ่งสามารถสรุปเป็นกราฟได้ดังภาพ

Claim: Variable array เมื่อมีการเพิ่มข้อมูลไป m ครั้งจะใช้เวลาทำงาน O(m) โดย amortized running time ของการเพิ่มข้อมูลคือ O(1)
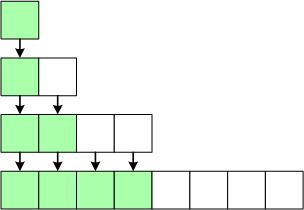
Proof: ในการคิดเวลาการทำงานล่วงหน้าของการเพิ่มข้อมูลแต่ละคั้งคิดเป็น 3 หน่วย โดยถ้าในเวลาที่ทำการเพิ่มข้อมูลโดยไม่มีการเพิ่มขนาดของ array จะมีการใช้เวลาในการทำงานจริง 1 หน่วย ซึ่งดังนั้นจะเหลือเวลาอีก 2 หน่วย แต่ในกรณีที่มีการขยายขนาดของ array จาก 2i เป็น 2i+1 จะมีการเพิ่มข้อมูลที่ไม่มีการ array 2i-1
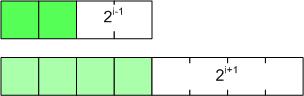
จะใช้เวลา 2 x 2i-1 = 2i
ดังนั้น การเพิ่มข้อมูล m ครั้ง ใช้เวลา 3m = O(m) หน่วย
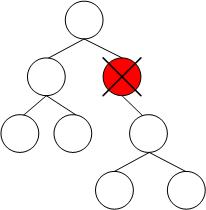
Delete Tree
การลบ Node ในต้นไม้มีวิธีการลบแบบหนึ่งที่เรียกว่า Lazy Delete มีวิธีการทำงานคือจะใช้การ Mark โหนดแทนการลบโหนดออกจากต้นไม้ โดยวิธีนี้จะเกิดปัญหาเมื่อมีการลบและ insert โหนดหลายๆครั้ง ส่งผลให้ต้นไม้มีความสูงมาก และไม่สามารถทำงานได้ภายในเวลา O(log n) เมื่อ N ≤ 2n
ในกรณีที่ N > 2n จะต้องมีการสร้างต้นไม้ขึ้นมาใหม่ โดยจะนำ Data ออกมาทั้งหมดและ Insert เข้าไปใหม่ ใช้เวลาทำงาน O(n)
จากข้างต้น กราฟในการทำงานของ Lazy Delete จะ peak เป็นช่วงๆ ซึ่งช่วงที่ peak จะเป็นช่วงที่มีการลบโหนด และเวลาในการทำงานจะคิดเฉลี่ยตามแบบการทำงานของ Amortized Analysis
ทบทวนความรู้เรื่อง Experiment, Expected value, Random variable
Experiment
- Event คือ เหตุการณ์ที่สนใจ
- Outcome คือ ผลลัพธ์ของเหตุการณ์ที่สนใจเป็น sub set ของ Sample space
- Sample space คือ set ของ outcome ที่เป็นไปได้
- Probability คือ ความน่าจะเป็น หมายถึง โอกาสที่จะเกิดเหตุการณ์ที่สนใจจากการทดลองสุ่มหนึ่งๆ เป็นจำนวนหรือค่าที่ไม่มีหน่วย เขียนแทนด้วย Pr(?) โดยที่ ? แทนด้วยชื่อของเหตุการณ์ที่สนใจ เช่น Pr [x=5] คือ ความน่าจะเป็นที่ x=5
สำหรับ ![]() โดยที่ A แทน Event เซตของ outcome จะได้ว่า
โดยที่ A แทน Event เซตของ outcome จะได้ว่า
1. ![]()
2. สำหรับ ![]()
3. สำหรับ ![]() ที่ disjoint กัน
ที่ disjoint กัน ![]()
ตัวอย่าง สมมุติให้มีถัง 3 ถัง
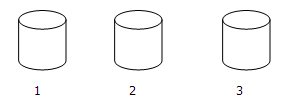
ให้ที่ถังแรกไม่มีลูกบอลหล่นลงไปเลย หาความน่าจะเป็น(Pr) ที่จะไม่มีลูกบอลหล่นลงในถังแรก
Ai คือ event ที่ลูกบอลลูกที่ i ไม่หล่นลงในถังใบแรก
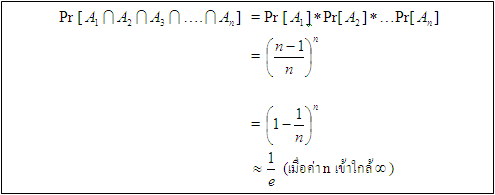
===Random Variable (ตัวแปรสุ่ม)=== คือ function หรือตัวแปรที่มีค่าขึ้นกับผลลัพธ์ (sample space) โดยจะรู้ค่าหลังจากการทดลอง
===Expected value (ค่าคาดหวัง)=== คือค่าเฉลี่ย โดยเฉลี่ยมีค่าเท่าไหร่ weight ตามความน่าจะเป็นที่จะได้ค่านั้น แทนด้วย E
นิยาม ตัวแปรสุ่ม X,![]()
ตัวอย่าง ถ้ามีถัง 3 ถัง บอล 2 ลูกสีดำ และสีขาว

หา Pr[X = i] จะได้ว่า

เอามาเป็นค่า weight ในการคำนวณ