204512-53/lecture11
'จดบันทึกคำบรรยายโดย:
นายชัชพล นุโยค รหัส 5214550049 (Part I) นายชัชพล นุโยค รหัส 5214550049 (Part I) นายสุรเดช วัฒนอุดมโรจน์ รหัส 5214550324 (Part I) นายชัยณรงค์ เหมือนรุ่ง รหัส 5214550057 (Part II) นายศศิน เทียนดี รหัส 5214550278 (Part II) น.ส.นันทณัฏฐ์ ภูทอง รหัส 5214550171 (Part II) น.ส.ชนาพร คุรุรัตน์พันธ์ รหัส 5214550031 (Part II)
Part I NP Completeness
NP: Non-deterministic Polynomial time คือ เซตของ Algorithm ที่ไม่สามารถแก้ไขปัญหาได้ในเวลาที่เป็น polynomial โดยการนิยามเซตของปัญหาเพื่อประโยชน์ในการเปรียบเทียบระดับความยาก-ง่ายของ Algorithm ซึ่งเซตของปัญหาสามารถแบ่งเป็นเซต P, NP, NP-hard และ NP-complete
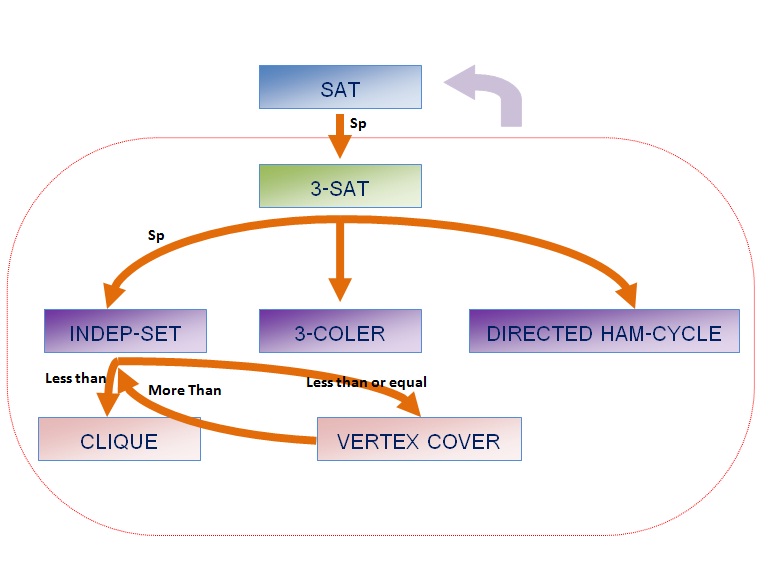
ในการเปรียบเทียบ Algorithm ใดๆ เราจะทำการพิจารณา Algorithm ว่าจัดอยู่ในเซตของปัญหาใด โดยใช้เทคนิคการลดรูปของปัญหา (Reduction) ว่าเป็นกลุ่มเดียวกับปัญหาที่อยู่ในเซตหรือไม่ ถ้าอยู่ในกลุ่มเดียวกันจะกล่าวว่า Algorithm มีความยากเท่ากัน ความยาก คือ มี Algorithm ที่มีประสิทธิภาพแก้ไขปัญหาหรือไม่
ปัญหา A สัมพันธ์ ปัญหา B
ปัญหา A ไม่ยากไปกว่า ปัญหา B
โดยมีความหมายว่า ถ้ามี Algorithm ที่สามารถแก้ปัญหา B ได้ ปัญหา A ก็จะสามารถแก้ได้เช่นกัน
ปัญหาที่ 1 : Independent Set เป็นปัญหากลุ่ม Decision Problem
นิยาม : ให้ Undirected graph G = (V, E) จะกล่าวว่า I ![]() V เป็น Independent Set ก็ต่อเมื่อ สำหรับทุกๆโหนด
U,V
V เป็น Independent Set ก็ต่อเมื่อ สำหรับทุกๆโหนด
U,V ![]() I, U
I, U ![]() V ไม่มีเส้นเชื่อมระหว่าง U และ V
V ไม่มีเส้นเชื่อมระหว่าง U และ V
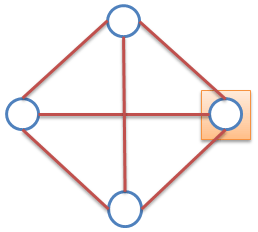
ปัญหา : ให้กราฟ G = (V, E) และ integer k, มี Independent set ขนาด ≥ k หรือไม่
ในภาพทำการเลือกโหนด (k) เท่ากับ 1 จะกล่าวว่ามี Independent set ขนาด 1
สามารถนำไปใช้แก้ปัญหา หาคนที่ไม่รู้จักกันในห้อง หรือ การเปิด-ปิดไฟแดงที่แยก
ปัญหาที่ 2 : Vertex Cover
นิยาม : C ![]() V เป็น Vertex Cover ก็ต่อเมื่อ
V เป็น Vertex Cover ก็ต่อเมื่อ ![]() (U,V)
(U,V)![]() E,U
E,U ![]() C หรือ V
C หรือ V ![]() C
C
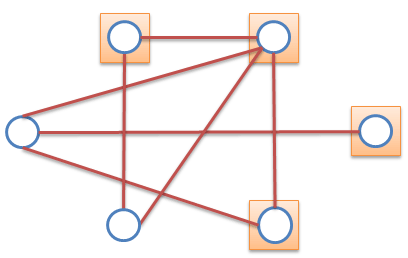
ปัญหา : ให้กราฟ G = (V, E) และ จำนวนเต็ม k ถามว่ามี vertex cover ขนาด ≤ k หรือไม่
ถ้าสมมติให้ Independent Set ![]() Vertex Cover
Vertex Cover
Lemma : พิจารณาเซต A ![]() V ใดๆ ให้ A เป็น imdenpendent set โดย V-A เป็น Vertec Cover
V ใดๆ ให้ A เป็น imdenpendent set โดย V-A เป็น Vertec Cover
Proof : Indenpendent set ![]() Vertex Cover
Vertex Cover
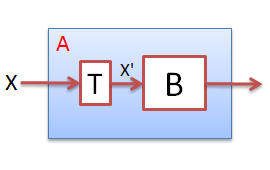
นิยาม : ปัญหา A เป็น Polynomial time เพื่อลดปัญหา B ถ้ามี Algorithm T ที่ทำงานใน Polynomial time สำหรับทุกๆ instance X ของ A จะได้ T(x) เป็น instance ของ B
X' = T(x) เป็น instance ของ B และ |X'| = Poly (|X|)
ถ้า x เป็น instance ตอบ "Yes" ใน A => x' เป็น instance ตอบ "Yes" ใน B
ถ้า x เป็น instance ตอบ "No" ใน A => x' เป็น instance ตอบ "No" ใน B
Lemma : ถ้า A ![]() B และมี Algorithm ที่แก้ปัญหา B ได้ใน Polynomial time จะมี Algorithm ที่แก้ปัญหา A ใน Polynomial time ได้ด้วย
B และมี Algorithm ที่แก้ปัญหา B ได้ใน Polynomial time จะมี Algorithm ที่แก้ปัญหา A ใน Polynomial time ได้ด้วย
Proof : ให้ M เป็น Polynomial time Algorithm ที่แก้ปัญหา B
จะได้ว่า A ![]() B
นั้นคือ มี Polynomial time Algorithm T ที่
B
นั้นคือ มี Polynomial time Algorithm T ที่ ![]() instance x ของ A
x' = T(x) มีขนาด poly(|x|) และคำตอบของ x ในปัญหา A ตรงกับของ x' ในปัญหา B
instance x ของ A
x' = T(x) มีขนาด poly(|x|) และคำตอบของ x ในปัญหา A ตรงกับของ x' ในปัญหา B
สำหรับ Algorithm M' ดังนี้
M'(x) : x' = T(x) return M(x')
แต่เนื่องจาก |x'| = poly(|x|)
ดังนั้น เวลาในการคำนวณ M(x')คือ poly(|x'|) = poly(poly(|x|)) = poly(|x|)
จากนิยาม M'(x) เป็นคำตอบของ x ใน A เหลือแต่ต้องตรวจสอบว่า M' ทำงานใน Polynomial time หรือ poly(|x|)
Part II
พิจารณา กราฟ G = (V,E) , CV เรียกว่า Clique ก็ต่อเมื่อ
u,v
C ที่ u
s (u,v)
E
CLIQUE
ให้กราฟ G = (V,E) และจำนวนเต็ม K กราฟ G clique = (V,E') เป็น Complement ของ G ถ้า (u,v)E <--> (u,v)
E'
Lemma กราฟ G = (V,E) มี Independent Set ขนาด K ใน G clique = (V,E') มี Clique ของ K
Proof (->)
ให้ I เป็น Independent Set ขนาด K ใน G
พิจารณาโหนด u,v  I ใดๆ ที่ u
I ใดๆ ที่ u v เนื่องจาก ณ เป็น Indep ใน G(u,v)
v เนื่องจาก ณ เป็น Indep ใน G(u,v)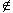 E
จากนิยามของ G clique , จะได้ว่า (u,v)
E
จากนิยามของ G clique , จะได้ว่า (u,v)  E clique
ดังนั้นทุกๆ u,v
E clique
ดังนั้นทุกๆ u,v  I ที่ u
I ที่ u v ,(u,v)
v ,(u,v) E Clique
E Clique