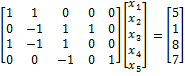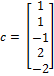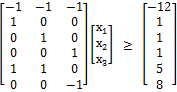204512/บรรยาย 10

บันทึกโดย : นายณัฐพล หล่อศิริ 50653781 , ...

Linear Programming

Note Problem ต่างจาก Instant ของ Problem กล่าวคือ Problem จะเท่ากับ เซตของ Instant ของ Problem
Note ตัวแปรทั้งหมดเป็นตัวแปรแบบเวกเตอร์ เพราะฉะนั้นจะขอละ ไม่ใส่เครื่องหมายเวกเตอร์

---

Optimization Problem

Instant ของปัญหา Optimization Problem จะประกอบด้วย

• set F (เซตของคำตอบที่เป็นไปได้)
• function cost F→R (จำนวนจริง)

ต้องการหา f∈F และ cost (f) ≤ cost (y) , สำหรับทุกๆ y∈F

---

Linear Programming Problem

Instant ของ linear programming คือ จำนวนเต็มบวก n, m, c ∈ R^n, b ∈ R^m และเมตริกซ์ A ของจำนวนจริงขนาด m x n จะได้ว่า

F = { x ← R^n :Ax = b , x ≥0 }

Cost : x → c^Tx

ตัวอย่าง

กำหนดให้ n = 3, m = 1 เขียนเป็นเมตริกซ์ ได้เป็น

หา x ที่ Ax = b ; x ≥ 0 แทนค่าจะได้

หา x ที่ทำให้ c1x1 + c2x2 + c3x3 น้อยที่สุด

ตัวอย่าง

• การเขียนในรูปแบบ สมการ
  

- การระบุเซต F (เป็น constraint ของปัญหา)

x1 + x2 = 5

x3 + x4 – x2 = 1

x1 - x2 + x3 = 8

x5 – x3 = 7

xi ≥ 0 ทุกๆ 1 ≤ i ≤5

- การระบุ c (เป็น objective ของปัญหา)

minimize: x1 + x2 – x3 + 2x4 – 2x5

• การเขียนในรูปแบบ เมตริกซ์
  

, ,

---

Form ของ Linear Programming

Standard form

เมตริกซ์

minimize: cx

subject to: Ax = b ; x ≥ 0

สมการ

minimize:

subject to: เมื่อ j = 1,…,n

Canonical form

เมตริกซ์

minimize: cx

subject to: Ax ≥ b ; x ≥ 0

สมการ

minimize:

subject to: เมื่อ j = 1,…,n

ตัวอย่าง

เตรียมสอบมีเวลาอ่านหนังสือ 12 ชม. มี 3 วิชา Architect, Algo, Soft Com. อ่านอย่างน้อยวิชาละ 1 ชม., อ่าน architect & algo รวมกันไม่น้อยกว่า 5 ชม., อ่าน Soft Com. ไม่เกิน 8 ชม.

ถ้าให้

x1 = เวลาอ่าน Architect

x2 = เวลาอ่าน Algo

x3 = เวลาอ่าน Soft Com.

ให้ความเหนื่อยในการอ่านเป็น x1 + 5x2 + 2x3
เป้าหมายคือ ต้องการอ่านหนังสือให้ได้ตามเงื่อนไข + ความเหนื่อยน้อยสุด
วิธีทำ

minimize: x1 + 5x2 + 2x3

subject to:

x1 + x2 + x3 ≤ 12

x1 ≥ 1

x2 ≥ 1

x3 ≥ 1

x1 + x2 ≥ 5

x1 , x2 , x3 ≥ 0

แปลงให้อยู่ในรูป canonical form การทำให้สมการที่เป็น ≤ ให้เป็น ≥ ให้หมดจะได้ว่า

minimize: x1 + 5x2 + 2x3

subject to:

-x1 - x2 - x3 ≥ -12

x1 ≥ 1

x2 ≥ 1

x3 ≥ 1

x1 + x2 ≥ 5

x1 , x2 , x3 ≥ 0

เขียนเป็น matrix ได้