418531 ภาคต้น 2552/โจทย์ปัญหาการพิสูจน์ II/เฉลยข้อ 2
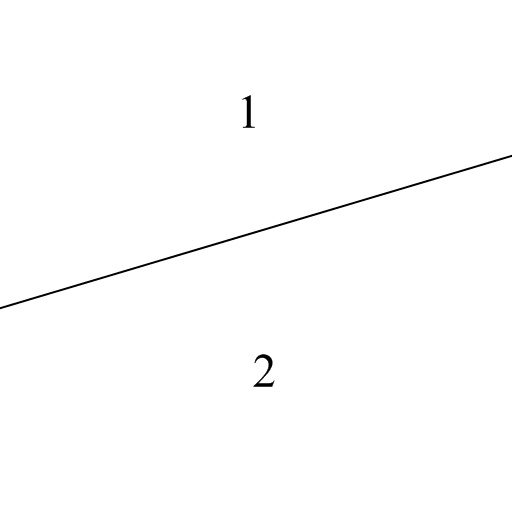
(Base Case) n มีค่าเท่ากับ 1 และเราได้ว่าเส้นตรง 1 เส้นแบ่งระนาบออกเป็น 2 ส่วน ดังภาพ
(Induction Case) ให้ n เป็นจำนวนเต็มบวก และสมมติให้เส้นตรง n เส้นใดๆ ที่ไม่มีเส้นสองเส้นใดๆ ขนานกัน และไม่มีเส้นสามเส้นใดๆ ตัดกันที่จุดจุดเดียว แบ่งระนาบออกเป็น ส่วน
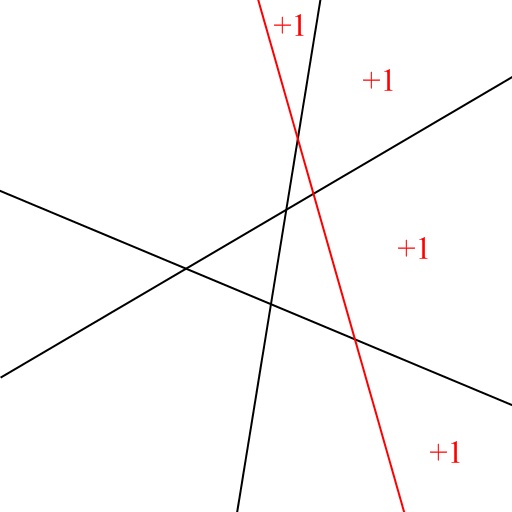
เมื่อเราลากเส้นตรงเส้นที่ n+1 เราจะได้ว่ามันจะตัดเส้นตรงอื่นๆ ที่มีอยู่แล้วทั้งหมด n เส้น กล่าวคือจะมีจุดตัดอยู่ทั้งหมด n จุด และจุดตัด n จุดนี้จะแบ่งเส้นตรงเส้นใหม่นี้ออกเป็น n+1 ส่วน ซึ่งส่วนทั้ง n+1 ส่วนนี้จะแบ่งพื้นที่ที่เคยมีอยู่แล้วออกเป็น 2 ส่วน ดังภาพ
ฉะนั้นจะได้ว่ามีพื้นที่ใหม่เกิดขึ้น n+1 ส่วน กล่าวคือจะมีพื้นที่ใหม่ทั้งหมด
ดังนั้นเราสามารถสรุปได้ว่าสำหรับจำนวนเต็ม n ใดๆ เส้นตรง n เส้นใดๆ ที่ไม่มีเส้นสองเส้นใดๆ ขนานกัน และไม่มีเส้นสามเส้นใดๆ ตัดกันที่จุดจุดเดียว แบ่งระนาบออกเป็น ส่วน