ชนิดของ edge ใน DFS tree (ค่ายวันที่ 11 มีนาคม 2551)

หลังจาก DFS บท directed graph เราสามารถแบ่ง edge ในกราฟออกได้เป็น 4 ประเภท ได้แก่

• Tree edge คือ edge ที่อยู่บน DFS tree ที่ได้จากการทำ DFS
• Back edge คือ edge ที่พุ่งออกจาก vertex ไปหาบรรพบุรุษของมันใน DFS tree
• Forward edge คือ edge ที่พุ่งออกจาก vertex ไปหาลูกหลานของมันใน DFS tree
• Cross edge คือ edge อื่นๆ ที่ไม่เข้าพวกทั้งสามข้างต้น

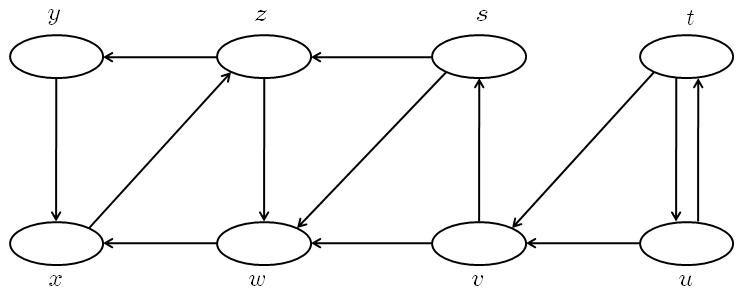
ยกตัวอย่างเช่น ในกราฟต่อไปนี้

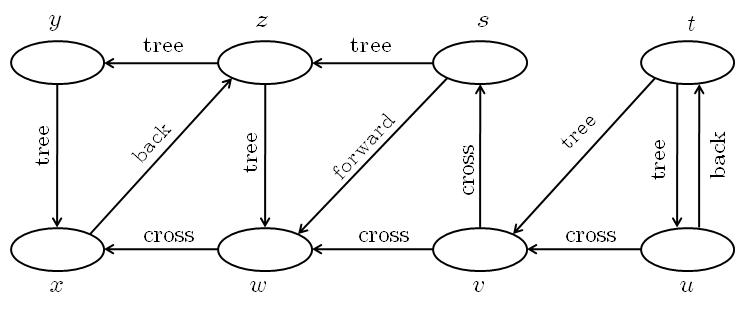
ถ้าเราทำ DFS โดยเดินผ่าน vertex ตามลำดับต่อไปนี้: s, z, y, x, w, t, v, u แล้ว edge ต่างๆ ในกราฟจะมีประเภทตามรูปข้างล่างนี้

แล้วจะรู้ได้อย่างไรว่า edge ไหนประเภทไหน?

Discover Time และ Finish Time

เราจะใช้สมบัติของ discovery time และ finish time ของ vertex ใน DFS forest มาช่วย

เวลาเราทำ DFS เรา save ค่าเวลาไว้ที่จุด $v\,$ ใดๆ ไว้สองค่า หนึ่งคือเวลา discovery time (เขียนแทนด้วย $d[v]\,$) และหนึ่งคือเวลา finish time (เขียนแทนด้วน $f[v]\,$) โดย

• $d[v]\,$ คือเวลาที่ DFS เดินมาถึง $v\,$ ครั้งแรก
• $f[v]\,$ คือเวลาที่ DFS สำรวจ $v\,$ และ vertex ที่ไปถึงจากมันได้จนหมดแล้ว กำลังจะ backtrack กลับออกไป

การบันทึกค่าเวลาทั้งสองสามารถทำได้ตาม pseudocode ต่อไปนี้: ให้มีตัวแปล global ชื่อ time แทนเวลาของระบบ

function DFS(v)
{
    time = time + 1
    d[v] = time
    visited[v] = true
  
    for edge (v,w) ทุกๆ edge
        if visited[w] == false
            DFS(w)
  
    time = time + 1
    f[v] = time
}

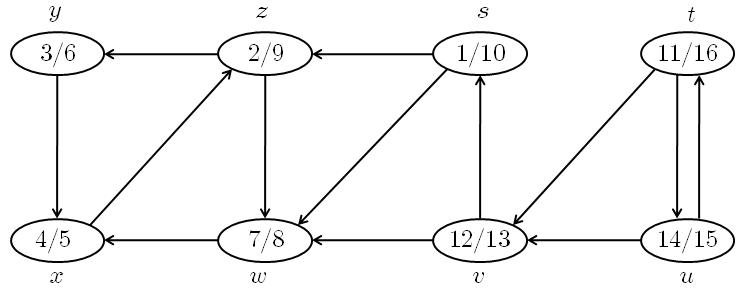
ยกตัวอย่างเช่น ถ้าเรานำอัลกอริทึมข้างต้นไปรันกับกราฟข้างบน เราจะได้ค่า $d[v]\,$ และ $f[v]\,$ ของแต่ละ vertex ดังต่อไปนี้ (เราเขียน $d[v]/f[v]\,$ ไว้ตรงกลาง vertex แต่ละ vertex)

สมบัติวงเล็บ

ค่า $d[v]\,$ และ $f[v]\,$ มีสมบัติที่สำคัญเรียกว่า สมบัติวงเล็บ ดังต่อไปนี้

ถ้า $u\,$ และ $v\,$ เป็น vertex สอง vertex ใดๆ ในกราฟแล้ว ภายในข้อเท็จจริงสามข้อต่อไปนี้ จะมีข้อเท็จจริงข้อหนึ่งเป็นจริง และมันจะเป็นจริงเพียงข้อเดียวเท่านั้น

1. $d[u]<d[v]<f[v]<f[u]\,$
2. $d[v]<d[u]<f[u]<f[v]\,$
3. ช่วง $[d[u],f[u]]\,$ และ $[d[v],f[v]]\,$ ไม่มีสมาชิกร่วมกันเลย

กรณีที่ 1 ตรงกับเหตุการณ์ที่ $u\,$ เป็นบรรพบุรุษของ $v\,$ ใน DFS tree กรณีที่ 2 ตรงกับเหตุการณ์ที่ $v\,$ เป็นบรรพบุรุษของ $v\,$ ส่วนกรณีที่ 3 ตรงกับเหตุการณ์ที่ไม่มีใครเป็นบรรพบุรุษใคร

แบ่งประเภทของ edge

สำหรับ edge $e=(u,v)\,$ ใดๆ เราสามารถใช้สมบัติวงเล็บข้างต้นในการจำแนกประเภทของมันได้

• ถ้า $d[u]<d[v]<f[v]<f[u]\,$ แสดงว่า $u\,$ เป็นบรรพบุรุษของ $v\,$ ฉะนั้น $e\,$ ต้องเป็น tree edge หรือ forward edge
• ถ้า $d[v]<d[u]<f[u]<f[v]\,$ แสดงว่า $v\,$ เป็นบรรพบุรุษของ $u\,$ ฉะนั้น $e\,$ ต้องเป็น back edge
• ถ้า $[d[u],f[u]]\,$ และ $[d[v],f[v]]\,$ แสดงว่าไม่มีใครเป็นบรรพบุรุษใคร ดังนั้น $e\,$ ต้องเป็น cross edge

ปัญหาที่เหลือคือ ในกรณีแรก เราจะแยกได้อย่างไรว่า edge ไหนเป็น tree edge และ edge ไหนเป็น forward edge? คำตอบคือเวลาทำ DFS ก็ให้ mark เอาไว้ว่า edge ไหนบ้างคือ tree edge แล้วก็ให้ไปเช็คที่ mark นั้นเอา

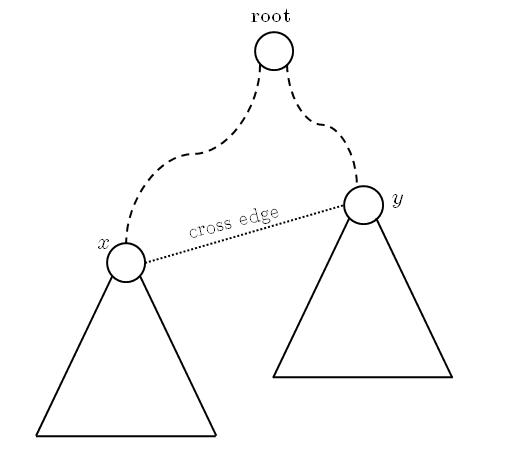
ชนิดของ edge ใน undirected graph

หากเราทำ DFS บน undirected graph เราสามารถแบ่ง edge ออกได้เป็นสองชนิดเท่านั้นคือ tree edge และ back edge

ทำไมถึงไม่มี forward edge หรือ cross edge เลย? ลองคิดดูว่าถ้ามี cross edge จะเกิดอะไรขึ้น

จากรูปข้างบน สมมติว่า DFS เดินทางจาก root ไปถึง x ก่อนแล้วค่อยไป y โดยเมื่อไปถึง y แล้วมันจึงเห็น x

หมายความว่า DFS(x) จะต้อง exit ก่อนที่ DFS(y) จะถูกเรียก

แต่นี่เป็นไปไม่ได้ เพราะถ้า DFS(x) ถูกเรียกแล้ว มันจะตรวจดู edge ทุก edge ที่ต่อกับ x ดังนั้นมันต้องเจอ y โดยผ่าน cross edge ที่เราคิดว่ามันมี ก่อนแล้วจึงเรียก DFS(y) ก่อน DFS(x) จะ exit ออกมา เกิดข้อขัดแย้ง

ดังนั้นจึงไม่มี cross edge ใน undirected graph

เราสามารถแสดงได้ว่าใน undirected graph ไม่มี forward edge ได้ด้วยการให้เหตุผลเดียวกัน