204512-53/lecture3

บันทึกคำบรรยายวิชา 204512-53 นี้ เป็นบันทึกที่นิสิตเขียนขึ้น เนื้อหาโดยมากยังไม่ผ่านการตรวจสอบอย่างละเอียด การนำไปใช้ควรระมัดระวัง

จดบันทึกคำบรรยายโดย:

นายดลวัฒน์ งามภักดิ์	5314550075
นายณรงค์ศักดิ์ ทิพย์จ้อย	5314552230
นายปริตร หมึ่นคง	5314552248

Red-Black Tree (Cont.)

• Tree ใดๆ จะเป็น Red-Black Tree ได้ต้องมีคุณสมบัติ 5 ข้อ ได้แก่

1. โหนดแต่ละโหนด เป็นได้เพียงสีใดสีหนึ่งเท่านั้น ระหว่าง สีแดง หรือ สีดำ
2. Root ต้องเป็นสีดำ
3. Leaf ปลายสุดทั้งหมดต้องเป็นสีดำ
4. โหนดที่มีสีแดง จะต้องมีโหนดลูกเป็นสีดำ ทั้ง 2 โหนด
5. จากโหนดใดๆ ไปหา Leaf ที่เป็นลูกหลานของตัวเอง จะต้องมีจำนวนโหนดสีดำเท่ากันหมด

ความสูงของ Red-Black Tree เป็น O(log n)

วิธีแก้ปัญหา เมื่อเพิ่ม Leaf Node เข้าไปใหม่ที่จุดใดจุดหนึ่ง ใน Leaf Node ที่เพิ่มเข้าไปใหม่ เราต้องทำการปรับสมดุลใหม่ โดยการตรวจสอบแล้วเปลี่ยนสีในบางจุดที่ต้องเปลี่ยนให้ตรงกับคุณสมบัติของ Red-Black Tree ทั้ง 5 ข้อไปเรื่อยๆ ไล่ตั้งแต่ Leaf Node ที่ได้ทำการเพิ่มเข้ามาขึ้นไปจนถึง Root

Divide and Conqure

เป็นยุทธศาสตร์ในการแก้ปัญหาด้วยอัลกอริทึมแบบหนึ่ง เช่น ถ้าต้องการหาข้อมูลอันหนึ่ง ให้จิ้มไปที่จุดกึ่งกลาง ถ้าเจอคำตอบก็จบ แต่ถ้าไม่เจอ เราก็เลือกว่าควรจะไปทางมากกว่าหรือน้อยกว่า (เนื่องจาก Binary Search นั้น ข้อมูลได้มีการเรียงกันก่อนอยู่แล้ว)

Concept – ตีเมืองใหญ่ให้เป็นเมืองเล็กก่อน

Review Merge Sort

1. จิ้มไปที่กึ่งกลางจะได้ array 2 ส่วน คือ Array A ขนาด n และ Array B ขนาด m
2. ซึ่ง array แต่ละส่วนจะทำการ Sort ใน Array ของตัวเอง เรียกว่า Merge Sort
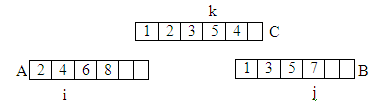
3. หลังจากนั้นทำการ เปรียบค่าแต่ละค่า ในแต่ละ Index ระหว่าง array ได้ค่าไหนที่น้อยกว่าก็ทำการ Add เข้าไปใน array ใหม่ ชื่อว่า C และทำไปเรื่อยๆ จนครบ เรียกว่า การ Merge

Algorithm

  เราจะได้อัลกอริทึมในการ Merge โดยให้ k=0, i=1, j=1

  1. While k < n+m 
  2.	 k $\Leftarrow$ k+1
  3.	if A[i] < B[j]
  4.		C[k] $\Leftarrow$ A[i]
  5.		i $\Leftarrow$i+1
  6.	else
  7.		C[k] $\Leftarrow$ B[j]
  8.		j $\Leftarrow$ j+1

Proof

 เราจะพิสูจน์ว่าอัลกอริทึมข้างบนถูกต้อง โดย
  *ถ้า array A เรียงจากน้อยไปหามาก และ
  *ถ้า array B เรียงจากน้อยไปหามาก แล้ว
  *Array C จะเป็น array ที่มาจาก array A และ array B ที่เรียงจากน้อยไปหามาก

Loop Invariants

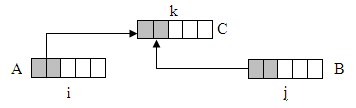
จาก C[1…k] มีข้อมูลของ A[1…i+1] และ B[1…j-1] และเรียงลำดับ

จะพิสูจน์ว่า array ชุดใหม่ มาจาก

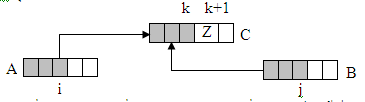
จะได้ว่า Z เป็นค่าใหญ่ที่สุดใน array A ที่ตำแหน่ง i แต่ปัญหาอยู่ที่ จะทำอย่างไรให้เห็นว่า Z มีค่ามากที่สุดใน array B ในตำแหน่ง j

จากรูปข้างบนแสดงให้เห็นว่า เงื่อนไขใน Loop Invariants ยังไม่แข็งแกร่งพอ โดยจะเพิ่มเงื่อนไขใหม่ได้เป็น จาก C[1…k] มีข้อมูลของ A[1…i+1] และ B[1…j-1] และเรียงลำดับ (เพิ่ม และข้อมูลทุกตัวใน C[1…k] น้อยกว่าหรือเท่ากับ A[i] และ B[j]

Trick หากเงื่อนไขของ Loop Invariants แรกยังไม่แข็งแกร่งพอ ก็ให้หาเงื่อนไขเพิ่มเติมที่รัดกุมกว่าเดิมใส่เข้าไปจนกว่าจะพิสูจน์ได้ ทำให้ได้ว่าอัลกอริทึมนี้ จะได้ Big O = O(m+n) ซึ่งวนลูปทั้งหมด m+n รอบ ซึ่งหลักๆแล้วเราจะดูที่เวลาการทำงานมากกว่า

Merge Sort Algorithm

  Merge Sort(A) ให้  n = ขนาดของ A                                                 $\Rightarrow$ ใช้เวลา T(n)
  A(left) $\Leftarrow$ A[1…(n/2)]          	                         $\Rightarrow$ ใช้เวลา O(n)
  A(right) $\Leftarrow$ A[(n+1)/2 …n] 			         $\Rightarrow$ ใช้เวลา O(n)
  
  Assume ว่า n เป็นกำลังของ 2
  
  S(left) $\Leftarrow$ Merge Sort(A(left))	                	 $\Rightarrow$ ใช้เวลา T(n/2)
  S(right) $\Leftarrow$ Merge Sort(A(right))		         $\Rightarrow$ ใช้เวลา T(n/2)
  S $\Leftarrow$ Merge Sort(S(left), S(right))		         $\Rightarrow$ ใช้เวลา O(n)
  Return S

   ให้ T(n) เป็นเวลาการทำงานที่แย่ที่สุด เมื่อ input ขนาด n โดยที่ O(n)+O(n) = O(n) ดังนั้น จะได้ T(n) = 2T(n/2) + O(n)

ปัญหาอยู่ที่อัลกอริทึมนี้ยังผิดอยู่ เพราะเนื่องจากยังไม่มี Base Case จึงไม่รู้ว่าจะต้องเริ่มทำ Loop เมื่อไร โดยในที่นี้ จะให้ Base Case เป็น T(1) = O(1) และให้ T(n) เป็น recurrence แต่เนื่องจาก O(n)+O(n)=O(n) นั้น ค่าคงที่บางส่วนจะหายไป ดังนั้นจึงเปลี่ยน T(n) ใหม่เป็น T(n) <= 2T(n/2) +Cn

Review Quick Sort

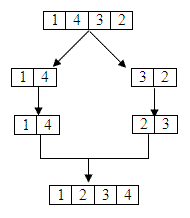
จากรูปเป็นตัวอย่างของข้อมูลที่จะทำการ Quick Sort โดยเริ่มต้น เราหาตัว pivot ก่อน

เมื่อเราได้ตัว pivot แล้ว ก็แยกตัว pivot ออกมา เราจะได้ ข้อมูลเป็น 2 ส่วน คือ ข้อมูลที่อยู่ฝั่งซ้ายและฝั่งขวา

แล้วเมื่อทำการ Quick Sort ในแต่ละฝั่ง จะได้ ข้อมูลที่เรียงแล้วในฝั่งของตนเอง

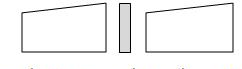
ซึ่ง Quick Sort จะต่างจาก Merge Sort ตรงที่ Merge Sort จะเริ่มจากจุดกึ่งกลาง แต่ Quick Sort จะต้องเริ่มหาตัว pivot ก่อน

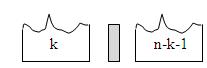
 จะใช้เวลา T(n) = O(n) + T(k) + T(n-k-1) โดยที่ในกรณีที่แย่ที่สุดนั้น จะได้ T(n) = O(n) + T(n-1)

การหาค่า pivot จะง่าย ก็ต่อเมื่อตัว pivot อยู่ตรงกลาง ซึ่งเราจะใช้วิธี Selection หาค่า Median

Selection

ให้ข้อมูล x1, x2, x3, … , xn และจำนวนเต็ม k ให้หาข้อมูลตัวที่น้อยที่สุด เป็นอันดับที่ k
ได้เวลา O(n log n) โดยใช้การ Merge Sort และหยิบตัวที่ k ซึ่งหากต้องการทำให้ได้ O(n) จะใช้การ Quick Selection

การ Quick Selection

ใช้เวลาเลือกตัว Pivot = O(x)

ใช้เวลาตรวจสอบว่าอยู่ฝั่งซ้ายหรือขวา = O(n)

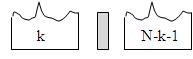
จะได้ว่า T(n) = O(x) + O(n) + T(n/2) เมื่อ T(n/2) เป็นเวลาที่ใช้ในการ recursive ฝั่งใดฝั่งหนึ่ง

  ดังนั้น เมื่อ 		T(1)  = 1
 			T(n)  = Cn + ((Cn/2) + T(n/4))
 			        = Cn + (Cn/2) + (Cn/4) + T(n/8)
 			        <= Cn[1+(1/2)+(1/4)+(1/8)+…]
  
  ซึ่ง [1+(1/2)+(1/4)+(1/8)+…] มีค่าได้ไม่เกิน 2
  ดังนั้น			           <= 2Cn	= O(n)

จากตัวอย่างนี้ โชคดีตรงที่ว่า ได้ค่าตรงกลางพอดี แต่ถ้าหากแบ่งได้ 1/10 แล้ว จะได้ใหม่ว่า

  			 T(1) = 1
  			 T(n) = Cn + T(9n/10)
  			        = Cn + (Cn(9/10) + T(n(9/10)^2))
  			        = Cn + Cn(9/10) + Cn(9/10)^2 + T(n(9/10)^3)
 			        <= 2Cn	= O(n)

Finding medians in linear time

เป็นอีกอัลกอริทึมหนึ่งสำหรับหาค่ากลางเหมือนกัน

• ในแต่ละแถว Sort ใช้เวลา C1
• เนื่องจากมี n/5 แถว จึงใช้เวลา ((C1*n)/5)
• หลัง Sort แล้วเอาข้อมูลตรงแถวกลางมาเป็นค่า Median

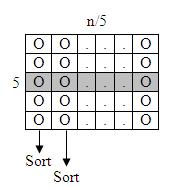
algorithm

   ดังนั้น ใช้เวลาทั้งหมด T(n) = Cn + T(n/5) + T(max(l, n-l))

จาก

ค่า Medium ที่เราได้ จะมากกว่าสมาชิกในช่องที่ 1 จำนวณ n/4 ตัว และจะน้อยกว่าช่อง 2 จำนวน n/4 ตัว ดังนั้น T(n) <= Cn + T(n/5) + T(3n/4)

Conclusion

 Base Case: 		T(1) = 1
 Merge Sort: 		T(n) = Cn + 2T(n/2)
 Quick Sort:		T(n) = Cn + T(1) + T(n-1)
 		        	        <= Cn + T(n-1)
 Selection:		T(n) <= Cn + T(n/5) + T(3n/4)
 Binary Search:		T(n) = 1+ T(n/2)

Polynomial Multiplication

จาก Polynomial: 
f(x) = a0x^0 + a1x^1 + a2x^2 + … + a(n-1)x^(n-1)
g(x) = b0x^0 + b1x^1 + b2x^2 + … + b(n-1)x^(n-1)

หากนำ polynomial ทั้งสองมาคูณกันแล้วใช้ Divide and conquer จะได้

	f(x) = x^((n-1)/2)A(x) + B(x)
	g(x) = x^(n/2)C(x) + D(x)
ดังนั้น f(x) * g(x) = x^n A(x)B(x) + x^(n/2) [A(x)D(x)+C(x)D(x)] + B(x)D(x)
ดังนั้น T(n) = 4T(n/2) + Cn

จะอธิบายโดยรูปได้ว่า หากเราทำการแบ่งข้อมูลในแต่ละครั้งออกเป็น 4 ส่วน จะได้ออกมาดังรูป

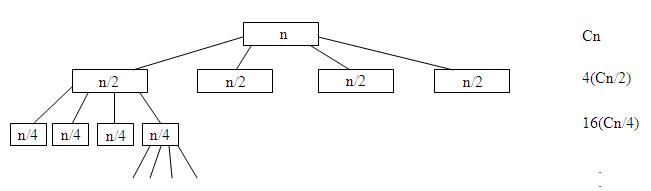
แต่ปัญหาของการใช้ Divide and Conqure ก็คือ ถึงแม้แต่ละชั้นจะใช้เวลา O(n) ก็ตาม แต่ชั้นสุดท้ายมีลูกมากเกินไป จึงได้ค่าออกมาเป็น O(n^2) = 2^(log n) Cn

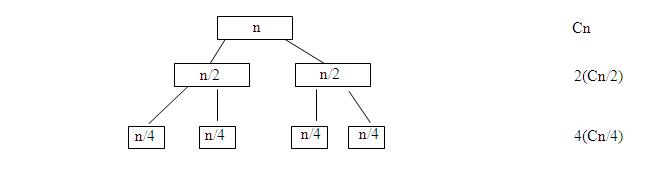
ดังนั้น จากรูปข้างบน หากเราแบ่งแต่ละชั้นออกเป็น 2 ส่วน จะได้เวลาเท่ากับ O(n log n)

และถ้าเราอยากให้เร็วขึ้นอีก เราก็จะให้แต่ละชั้นมีเพียงส่วนเดียว เราก็จะได้เวลาเท่ากับ O(n)