บันทึกคำบรรยายวิชา 204512-53 นี้ เป็นบันทึกที่นิสิตเขียนขึ้น เนื้อหาโดยมากยังไม่ผ่านการตรวจสอบอย่างละเอียด การนำไปใช้ควรระมัดระวัง

จดบันทึกคำบรรยายโดย: (กรุณาใส่ด้วย) Algorithm Lecture #1

เนื้อหา

1 Course Information
- 1.1 เกณฑ์การให้คะแนน
2 Introduction to Algorithm
- 2.1 ทำไมเราต้องวิเคราะห์อัลกอริทึม
- 2.2 เนื้อหาแต่ละบทที่จะสอน ตามลำดับ
  - 2.2.1 Data Structure

Course Information

รายละเอียดวิชาสามารถดูได้ที่ http://www.cpe.ku.ac.th/~jtf/wiki/doku.php?id=01204512-53

เกณฑ์การให้คะแนน

Homework 15%
Project 15%
Scribe Note 5%
Mid-Term 2 Times 20*2%
Final 25%

Introduction to Algorithm

ทำไมเราต้องวิเคราะห์อัลกอริทึม

เพื่อความถูกต้องของอัลกอริทึม - ต้องการความแน่ใจ
เพื่อประสิทธิภาพของอัลกอริทึม
- เวลา (time)
- พื้นที่ (space)
- คุณภาพคำตอบ (quality)

เนื้อหาแต่ละบทที่จะสอน ตามลำดับ

Data Structure
Graph Algorithm
Dynamic Programming
Linear Programming
Randomize Algorithm

Data Structure

ตัวอย่างปัญหาที่ 1

การจองอาเรย์ให้เหมาะสมกับขนาดข้อมูลที่บรรจุ โดยกำหนดให้มีขั้นตอน การทำงานดังนี้

จองพื้นที่สำหรับใส่ของ
นำของไปใส่จนเต็ม
จองพื้นที่เพิ่มสำหรับใส่ของ

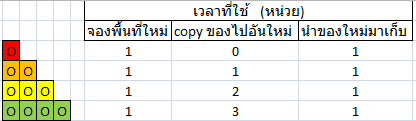
กรณี 1: จองแบบเพิ่มทีละ 1 ที่

จากภาพการเก็บ สามารถวิเคราะห์ได้ว่า

การจองใช้เวลา 1 หน่วย
การคัดลอกต้องคัดลอก i - 1 ตัวดังนั้นใช้เวลา i - 1 หน่วย
การนำข้อมูลใหม่ไปใส่ใช้เวลาอีก 1 หน่วย

จะเห็นได้ว่าในการสร้างอาเรย์เก็บข้อมูล n ตัวจะต้องใช้เวลาทั้งหมด

=  $2+3+4+...+n+n+1$  หน่วย
=  $2+3+4+...+n+n+1$  หน่วย
=  $(1+2+3+...+n)+n$  หน่วย

ดังนั้นการถ้ามีข้อมูล n ตัวจะได้ว่าต้องใช้ หน่วย หรือ O( $Wikimedia Error * { margin: 0; padding: 0; } body { background: #fff; font: 15px/1.6 sans-serif; color: #333; } .content { margin: 7% auto 0; padding: 2em 1em 1em; max-width: 640px; display: flex; flex-direction: row; flex-wrap: wrap; } .footer { clear: both; margin-top: 14%; border-top: 1px solid #e5e5e5; background: #f9f9f9; padding: 2em 0; font-size: 0.8em; text-align: center; } img { margin: 0 2em 2em 0; } a img { border: 0; } h1 { margin-top: 1em; font-size: 1.2em; } .content-text { flex: 1; } p { margin: 0.7em 0 1em 0; } a { color: #0645ad; text-decoration: none; } a:hover { text-decoration: underline; } code { font-family: sans-serif; } summary { font-weight: bold; cursor: pointer; } details[open] { background: #970302; color: #dfdedd; } .text-muted { color: #777; } @media (prefers-color-scheme: dark) { a { color: #9e9eff; } body { background: transparent; color: #ddd; } .footer { border-top: 1px solid #444; background: #060606; } #logo { filter: invert(1) hue-rotate(180deg); } .text-muted { color: #888; } }$

Error

Too many requests (f061ab2)

n^{2}

)

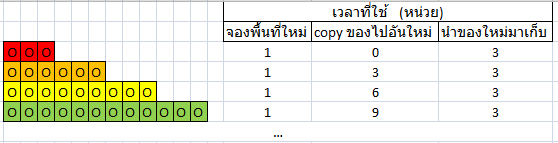
กรณี 2: จองแบบเพิ่มทีละ 3 ที่

จากภาพการเก็บ สามารถวิเคราะห์ได้ว่าจะยังได้ผลลัพธ์ไม่ต่างจากเดิมมาก คือ O( $Wikimedia Error * { margin: 0; padding: 0; } body { background: #fff; font: 15px/1.6 sans-serif; color: #333; } .content { margin: 7% auto 0; padding: 2em 1em 1em; max-width: 640px; display: flex; flex-direction: row; flex-wrap: wrap; } .footer { clear: both; margin-top: 14%; border-top: 1px solid #e5e5e5; background: #f9f9f9; padding: 2em 0; font-size: 0.8em; text-align: center; } img { margin: 0 2em 2em 0; } a img { border: 0; } h1 { margin-top: 1em; font-size: 1.2em; } .content-text { flex: 1; } p { margin: 0.7em 0 1em 0; } a { color: #0645ad; text-decoration: none; } a:hover { text-decoration: underline; } code { font-family: sans-serif; } summary { font-weight: bold; cursor: pointer; } details[open] { background: #970302; color: #dfdedd; } .text-muted { color: #777; } @media (prefers-color-scheme: dark) { a { color: #9e9eff; } body { background: transparent; color: #ddd; } .footer { border-top: 1px solid #444; background: #060606; } #logo { filter: invert(1) hue-rotate(180deg); } .text-muted { color: #888; } }$

Error

Too many requests (f061ab2)

n^{2}

) โดย n ในที่นี้เทียบได้กับ

{\frac {n}{3}}

ของตัวอย่างบน มาจาก

Wikimedia Error * { margin: 0; padding: 0; } body { background: #fff; font: 15px/1.6 sans-serif; color: #333; } .content { margin: 7% auto 0; padding: 2em 1em 1em; max-width: 640px; display: flex; flex-direction: row; flex-wrap: wrap; } .footer { clear: both; margin-top: 14%; border-top: 1px solid #e5e5e5; background: #f9f9f9; padding: 2em 0; font-size: 0.8em; text-align: center; } img { margin: 0 2em 2em 0; } a img { border: 0; } h1 { margin-top: 1em; font-size: 1.2em; } .content-text { flex: 1; } p { margin: 0.7em 0 1em 0; } a { color: #0645ad; text-decoration: none; } a:hover { text-decoration: underline; } code { font-family: sans-serif; } summary { font-weight: bold; cursor: pointer; } details[open] { background: #970302; color: #dfdedd; } .text-muted { color: #777; } @media (prefers-color-scheme: dark) { a { color: #9e9eff; } body { background: transparent; color: #ddd; } .footer { border-top: 1px solid #444; background: #060606; } #logo { filter: invert(1) hue-rotate(180deg); } .text-muted { color: #888; } } Error Too many requests (f061ab2) If you report this error to the Wikimedia System Administrators, please include the details below. Request served via cp5021 cp5021, Varnish XID 130003511 Upstream caches: cp5021 int Error: 429, Too many requests (f061ab2) at Fri, 30 Jan 2026 20:45:31 GMT Sensitive client information IP address: 158.108.32.49

ซึ่งมี factor 3 เพิ่มเข้ามา

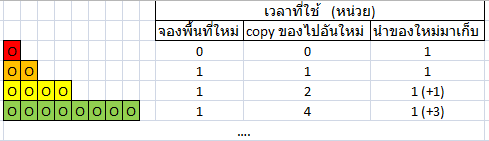
กรณี 3: จองแบบเพิ่มทีละ $2^{k}$ ที่

ต่อมามีคนเสนอว่าถ้าลองจองเป็นแบบ $2^{k}$ โดยที่ k หมายถึงการจองครั้งที่ k และค่า k เริ่มต้นจาก 0 เพื่อเป็นการตัดปัญหา ว่ากรณ๊ถ้าจองไม่เต็มจะทำอย่างไร เราจึงสมมุติไปเลยว่าการจองที่ n นั้นจะต้องจอง $Wikimedia Error * { margin: 0; padding: 0; } body { background: #fff; font: 15px/1.6 sans-serif; color: #333; } .content { margin: 7% auto 0; padding: 2em 1em 1em; max-width: 640px; display: flex; flex-direction: row; flex-wrap: wrap; } .footer { clear: both; margin-top: 14%; border-top: 1px solid #e5e5e5; background: #f9f9f9; padding: 2em 0; font-size: 0.8em; text-align: center; } img { margin: 0 2em 2em 0; } a img { border: 0; } h1 { margin-top: 1em; font-size: 1.2em; } .content-text { flex: 1; } p { margin: 0.7em 0 1em 0; } a { color: #0645ad; text-decoration: none; } a:hover { text-decoration: underline; } code { font-family: sans-serif; } summary { font-weight: bold; cursor: pointer; } details[open] { background: #970302; color: #dfdedd; } .text-muted { color: #777; } @media (prefers-color-scheme: dark) { a { color: #9e9eff; } body { background: transparent; color: #ddd; } .footer { border-top: 1px solid #444; background: #060606; } #logo { filter: invert(1) hue-rotate(180deg); } .text-muted { color: #888; } }$

Error

Too many requests (f061ab2)

n=2^{k}

โดย k นั้นคือเลขจำนวนเต็มใดๆที่มากกว่า 0 ซึ่งถ้า

Wikimedia Error * { margin: 0; padding: 0; } body { background: #fff; font: 15px/1.6 sans-serif; color: #333; } .content { margin: 7% auto 0; padding: 2em 1em 1em; max-width: 640px; display: flex; flex-direction: row; flex-wrap: wrap; } .footer { clear: both; margin-top: 14%; border-top: 1px solid #e5e5e5; background: #f9f9f9; padding: 2em 0; font-size: 0.8em; text-align: center; } img { margin: 0 2em 2em 0; } a img { border: 0; } h1 { margin-top: 1em; font-size: 1.2em; } .content-text { flex: 1; } p { margin: 0.7em 0 1em 0; } a { color: #0645ad; text-decoration: none; } a:hover { text-decoration: underline; } code { font-family: sans-serif; } summary { font-weight: bold; cursor: pointer; } details[open] { background: #970302; color: #dfdedd; } .text-muted { color: #777; } @media (prefers-color-scheme: dark) { a { color: #9e9eff; } body { background: transparent; color: #ddd; } .footer { border-top: 1px solid #444; background: #060606; } #logo { filter: invert(1) hue-rotate(180deg); } .text-muted { color: #888; } } Error Too many requests (f061ab2) If you report this error to the Wikimedia System Administrators, please include the details below. Request served via cp5021 cp5021, Varnish XID 147035786 Upstream caches: cp5021 int Error: 429, Too many requests (f061ab2) at Fri, 30 Jan 2026 20:45:32 GMT Sensitive client information IP address: 158.108.32.49

อาจหมายถึงการแถมเวลาให้เต็ม

n=2^{k}

เลยก็ได้

จากภาพการเก็บ สามารถวิเคราะห์ได้ว่า

จะได้ว่ามีการจองข้อมูลเกิดขึ้นทั้งหมด k ครั้ง
มีการเขียนข้อมูล $n(2^{k})$ ครั้ง
มีการคัดลอกข้อมูล $Wikimedia Error * { margin: 0; padding: 0; } body { background: #fff; font: 15px/1.6 sans-serif; color: #333; } .content { margin: 7% auto 0; padding: 2em 1em 1em; max-width: 640px; display: flex; flex-direction: row; flex-wrap: wrap; } .footer { clear: both; margin-top: 14%; border-top: 1px solid #e5e5e5; background: #f9f9f9; padding: 2em 0; font-size: 0.8em; text-align: center; } img { margin: 0 2em 2em 0; } a img { border: 0; } h1 { margin-top: 1em; font-size: 1.2em; } .content-text { flex: 1; } p { margin: 0.7em 0 1em 0; } a { color: #0645ad; text-decoration: none; } a:hover { text-decoration: underline; } code { font-family: sans-serif; } summary { font-weight: bold; cursor: pointer; } details[open] { background: #970302; color: #dfdedd; } .text-muted { color: #777; } @media (prefers-color-scheme: dark) { a { color: #9e9eff; } body { background: transparent; color: #ddd; } .footer { border-top: 1px solid #444; background: #060606; } #logo { filter: invert(1) hue-rotate(180deg); } .text-muted { color: #888; } } Error Too many requests (f061ab2) If you report this error to the Wikimedia System Administrators, please include the details below. Request served via cp5021 cp5021, Varnish XID 148836722 Upstream caches: cp5021 int Error: 429, Too many requests (f061ab2) at Fri, 30 Jan 2026 20:45:33 GMT Sensitive client information IP address: 158.108.32.49$ (มองง่ายๆให้มองเป็นการบวกเลข binary)

ดังนั้นจะได้ k $Wikimedia Error * { margin: 0; padding: 0; } body { background: #fff; font: 15px/1.6 sans-serif; color: #333; } .content { margin: 7% auto 0; padding: 2em 1em 1em; max-width: 640px; display: flex; flex-direction: row; flex-wrap: wrap; } .footer { clear: both; margin-top: 14%; border-top: 1px solid #e5e5e5; background: #f9f9f9; padding: 2em 0; font-size: 0.8em; text-align: center; } img { margin: 0 2em 2em 0; } a img { border: 0; } h1 { margin-top: 1em; font-size: 1.2em; } .content-text { flex: 1; } p { margin: 0.7em 0 1em 0; } a { color: #0645ad; text-decoration: none; } a:hover { text-decoration: underline; } code { font-family: sans-serif; } summary { font-weight: bold; cursor: pointer; } details[open] { background: #970302; color: #dfdedd; } .text-muted { color: #777; } @media (prefers-color-scheme: dark) { a { color: #9e9eff; } body { background: transparent; color: #ddd; } .footer { border-top: 1px solid #444; background: #060606; } #logo { filter: invert(1) hue-rotate(180deg); } .text-muted { color: #888; } }$

Error

Too many requests (f061ab2)

+2^{k}+2^{k}-1=O(n)

ตัวอย่างปัญหาที่ 2

ในแต่ละ Network (เครือข่าย) ประกอบไปด้วยส่วนหลักๆ คือ Router, Client และ Routing table เราต้องการเรียนรู้การเชื่อมต่อของ Router แต่ละตัวเพื่อบันทึกใน Routing table การคิดวิธีการเพื่อแก้ปัญหา เราจะต้อง Assume (สมมติ) อย่างน้อยว่าการทำงานของระบบจะสำเร็จในสักวัน, ระบบมีความก้าวหน้า, ก้าวหน้ามากพอที่จะสำเร็จในช่วงเวลาที่รับได้ และสมมติฐานในปัจจัยอื่นๆ

การ ออกแบบ Routing table แบบ RIP

Assume ว่า Router ทุกตัวทำการ Broadcast (กระจายสัญญาณไปหาทุกตัว) พร้อมกัน และ Router ทุกตัวรู้จักตัวเอง ในที่นี้ให้ค่าระยะของเส้นเชื่อม (edge) เท่ากับ 1 หน่วย
RIP เป็นการหาเส้นเชื่อมระหว่าง Router เพื่อให้สื่อสารถึงกันได้ทั้งหมด โดยมีค่าระยะทางน้อยที่สุด
ในการคิดครั้งนี้จะคิดโดยใช้ Router A เป็นโหนดตั้งต้น แล้วค้นหา Router ตัวอื่นที่อยู่รอบๆ

กำหนดให้

Set ของโหนด ทั้งหมด แทนด้วย V จะได้ว่า V = {A, B, C, ..., H}
Set ของเส้นเชื่อม ทั้งหมด แทนด้วย E จะได้ว่า E = {(A,D), (A,B), (A,E), ..., (F,H)}
Set ของโหนด ที่อยู่ในชั้น n (ติดต่อกับ A ด้วยระยะทาง n หน่วย) แทนด้วย Ln

จะได้ว่า

L0 = {A}, L1 = {v e V-L0 | มี node u ที่ u e L0 และ (u,v) e E}

ดังนั้นสำหรับค่า i ใดๆ ที่ i > 0, Li = {v e V - (ตั้งแต่ L0 จน Li - 1) | มี node u ที่ u e Li - 1 และ (u,v) e E} โดย กำหนดให้ L0={A}

ตัวอย่างปัญหาที่ 3

สำหรับลำดับจำนวนเต็ม i ใดๆ "P(i) ที่ $1+3+5+9+...+(2i-1)=i^{2}$ "

การพิสูจน์โดยใช้วิธี Induction นั้นแบ่งเป็น 2 ส่วนคือ

Basic step (Base case) ซึ่งเป็นจุดกำหนิดของตัวแรกของการคิด ส่วนใหญ่คือค่า 0 หรือ 1 โดยส่วนมากมักจะมีค่าจริงอยู่แล้ว
Inductive step โดยจะสมมติให้ P(i) มีค่าเป็นจริง แล้วต้องพิสูจน์ให้ได้ว่า P(i + 1) นั้นมีค่าเป็นจริง

วิธีการแก้ปัญหาในตัวอย่างนี้

Basic Step

$P(1)=1=1^{2}$ มีค่าเป็นจริง

Inductive Step

ถ้าให้ P(i) ที่ $1+3+5+9+...+(2i-1)=i^{2}$ เป็นจริงแล้ว ต้องพิสูจน์ว่า $P(i+1)$ ที่ เป็นจริง

$Wikimedia Error * { margin: 0; padding: 0; } body { background: #fff; font: 15px/1.6 sans-serif; color: #333; } .content { margin: 7% auto 0; padding: 2em 1em 1em; max-width: 640px; display: flex; flex-direction: row; flex-wrap: wrap; } .footer { clear: both; margin-top: 14%; border-top: 1px solid #e5e5e5; background: #f9f9f9; padding: 2em 0; font-size: 0.8em; text-align: center; } img { margin: 0 2em 2em 0; } a img { border: 0; } h1 { margin-top: 1em; font-size: 1.2em; } .content-text { flex: 1; } p { margin: 0.7em 0 1em 0; } a { color: #0645ad; text-decoration: none; } a:hover { text-decoration: underline; } code { font-family: sans-serif; } summary { font-weight: bold; cursor: pointer; } details[open] { background: #970302; color: #dfdedd; } .text-muted { color: #777; } @media (prefers-color-scheme: dark) { a { color: #9e9eff; } body { background: transparent; color: #ddd; } .footer { border-top: 1px solid #444; background: #060606; } #logo { filter: invert(1) hue-rotate(180deg); } .text-muted { color: #888; } }$

Error

Too many requests (f061ab2)

P(i+1)=P(i)+(2(i+1)-1)=P(i)+2i+1

แทนค่า $P(i)=i^{2}$ จะได้ $Wikimedia Error * { margin: 0; padding: 0; } body { background: #fff; font: 15px/1.6 sans-serif; color: #333; } .content { margin: 7% auto 0; padding: 2em 1em 1em; max-width: 640px; display: flex; flex-direction: row; flex-wrap: wrap; } .footer { clear: both; margin-top: 14%; border-top: 1px solid #e5e5e5; background: #f9f9f9; padding: 2em 0; font-size: 0.8em; text-align: center; } img { margin: 0 2em 2em 0; } a img { border: 0; } h1 { margin-top: 1em; font-size: 1.2em; } .content-text { flex: 1; } p { margin: 0.7em 0 1em 0; } a { color: #0645ad; text-decoration: none; } a:hover { text-decoration: underline; } code { font-family: sans-serif; } summary { font-weight: bold; cursor: pointer; } details[open] { background: #970302; color: #dfdedd; } .text-muted { color: #777; } @media (prefers-color-scheme: dark) { a { color: #9e9eff; } body { background: transparent; color: #ddd; } .footer { border-top: 1px solid #444; background: #060606; } #logo { filter: invert(1) hue-rotate(180deg); } .text-muted { color: #888; } }$

Error

Too many requests (f061ab2)

P(i+1)=i^{2}+2i+1=(i+1)^{2}

แสดงว่า $P(i+1)$ ที่ $Wikimedia Error * { margin: 0; padding: 0; } body { background: #fff; font: 15px/1.6 sans-serif; color: #333; } .content { margin: 7% auto 0; padding: 2em 1em 1em; max-width: 640px; display: flex; flex-direction: row; flex-wrap: wrap; } .footer { clear: both; margin-top: 14%; border-top: 1px solid #e5e5e5; background: #f9f9f9; padding: 2em 0; font-size: 0.8em; text-align: center; } img { margin: 0 2em 2em 0; } a img { border: 0; } h1 { margin-top: 1em; font-size: 1.2em; } .content-text { flex: 1; } p { margin: 0.7em 0 1em 0; } a { color: #0645ad; text-decoration: none; } a:hover { text-decoration: underline; } code { font-family: sans-serif; } summary { font-weight: bold; cursor: pointer; } details[open] { background: #970302; color: #dfdedd; } .text-muted { color: #777; } @media (prefers-color-scheme: dark) { a { color: #9e9eff; } body { background: transparent; color: #ddd; } .footer { border-top: 1px solid #444; background: #060606; } #logo { filter: invert(1) hue-rotate(180deg); } .text-muted { color: #888; } }$

Error

Too many requests (f061ab2)

1+3+5+9+...+(2(i+1)-1)=(i+1)^{2}

เป็นจริง

เพราะฉะนั้นพิสูจน์ ได้ว่า สำหรับลำดับจำนวนเต็ม i ใดๆ "P(i) ที่ $1+3+5+9+...+(2i-1)=i^{2}$ " เป็นจริง โดยใช้วิธีพิสูจน์แบบ induction

ตัวอย่างปัญหาที่ 4

ปัญหาการระบายสี Planar Graph ให้แต่ละเมืองแทนด้วยโหนด และเมืองที่มีอาณาเขตติดกันให้ลากเส้นเชื่อมติดต่อกัน

ทฤษฎีบท 4 สี - สามารถระบายสีโดยใช้สีไม่เกิน 4 สีบน Planar Graph
ทฤษฎีบท 5 สี - สามารถระบายสีโดยใช้สีไม่เกิน 5 สีบน Planar Graph

การพิสูจน์ทฤษฎีบท 5 สี

กำหนดให้

n แทนจำนวนโหนดในกราฟ
m แทนจำนวนเส้นเชื่อมในกราฟ
f แทนจำนวนหน้า (face)
degree(v) แทนดีกรีของโหนด v (ดีกรีของโหนด = จำนวนเส้นเชื่อมที่เชื่อมกับโหนดอื่นๆ ไม่นับเส้นเชื่อมวกกลับเข้าหาตัวเอง)

จากความจริงที่ว่า E(v ∈ G) degree(v) = 2*m (ค่ารวมของค่าดีกรีของทุกโหนด จะเป็นสองเท่าของจำนวนเส้นเชื่อมทั้งหมดในกราฟ)

Assume: n-m+f = 2
ลองให้ f = 3; $3*f<=2m$ , $f<={\tfrac {2*m}{3}}$ ,

204512-53/lecture1

เนื้อหา

Course Information

เกณฑ์การให้คะแนน

Introduction to Algorithm

ทำไมเราต้องวิเคราะห์อัลกอริทึม