204111:lab6

ปฏิบัติการที่ 6 ของวิชา 20411 ตามแผนร่างหัวข้อวิชา 204111 ส่วนรวมเนื้อหา

ทบทวนง่าย

ราคาพิเศษ

ร้านขายหนังสือร้านหนึ่ง พยายามเพิ่มยอดขายโดยการเสนอโปรโมชั่นพิเศษ ถ้าคุณซื้อหนังสือมากกว่า 3 เล่ม ที่มีมูลค่ารวมเกิน 500 บาท คุณจะได้ส่วนลด 10%

ให้เขียนโปรแกรมรับจำนวนหนังสือที่ซื้อและราคารวม จากนั้นคำนวณราคาที่ต้องจ่าย

ตัวอย่างการทำงาน 1

How many books: 2
How much: 1000
You have to pay 1000 bath.

ตัวอย่างการทำงาน 2

How many books: 5
How much: 500
You have to pay 500 bath.

ตัวอย่างการทำงาน 3

How many books: 5
How much: 600
You have to pay 540 bath.

พิมพ์เลขที่หารลงตัว

ให้เขียนโปรแกรมรับจำนวนเต็ม N และ K จากนั้นพิมพ์เลขตั้งแต่ 1 ถึง N ที่ K หารลงตัว

ตัวอย่างการทำงาน

Enter N: 10
Enter K: 3
3
6
9

แสดงรายการคูณสอง

เขียนฟังก์ชัน printdouble(s) ที่รับรายการ s ของจำนวนเต็ม จากนั้นให้พิจารณาข้อมูลในรายการทีละตัวตามลำดับ แล้วพิมพ์ค่าข้อมูลแต่ละตัวนั้นคูณด้วย 2

ตัวอย่างการทำงานใน Python shell (ให้นิสิตเขียนฟังก์ชันใน editor ของ Wing IDE จากนั้นกด Run แล้วทดลองเรียกใช้ฟังก์ชันใน Python Shell)

>>> printdouble([1,10,3,7,15])
2
20
6
14
30

Monte Carlo

ในส่วนนี้เราจะเขียนโปรแกรมเพื่อหาพื้นที่ใต้เส้นโค้ง โดยใช้การประมาณอีกวิธีหนึ่ง

แนวคิดของการประมาณด้วยวิธีการ Monte Carlo คือ เราจะพิจารณาพื้นที่สี่เหลี่ยมที่ครอบคลุมพื้นที่ใต้เส้นโค้งทั้งหมด จากนั้นเราจะสุ่มจุดจำนวนมาก ๆ ลงไปแล้วหาว่าจุดเหล่านั้น จุดใดอยู่ใต้เส้นโค้งบ้าง เพื่อประมาณว่างพื้นที่ใต้เส้นโค้งมีอัตราส่วนเป็นเท่าใดของพื้นที่ทั้งหมด

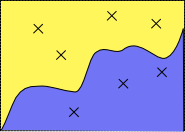
ยกตัวอย่างดังรูปด้านล่าง

เราสุ่มจุด 7 จุด อยู่ภายใต้เส้นโค้ง 3 จุด ดังนั้นเราจะประมาณว่าพื้นที่ใต้เส้นโค้งเป็น 3/7 = 0.4286 เท่า ของพื้นที่ทั้งหมด ถ้าเราทราบพื้นที่ทั้งหมด เราก็จะประมาณพื้นที่ใต้เส้นโค้งได้

เราจะสนใจฟังก์ชันเดียวกับในการบรรยายคือ $f(x)=x^{2}\cdot (2-2^{-x/100})$ และต้องการหาพื้นที่ใต้ฟังก์ชัน f ตั้งแต่ x = a ถึง x = b หรือ $\int _{a}^{b}x^{2}(2-2^{-x/100})dx$

(หมายเหตุถึง TA: ให้ลอกคำบรรยายตอนต้นนี้ไปใส่ที่ต้นโจทย์ย่อยทุกข้อ สามารถลิงก์รูปมาที่รูปด้านบนได้ และสามารถกด [แก้ไข] ที่หน้านี้เพื่อคัดลอกโค้ดส่วนที่เป็นสมการได้)

คำนวณฟังก์ชัน

ให้เขียนฟังก์ชัน func(x) ที่คำนวณค่า $f(x)=x^{2}\cdot (2-2^{-x/100})$

ตัวอย่างการทำงานใน Python Shell

>>> print(func(0))
0.0
>>> print(func(10))
106.696700846
>>> print(func(20))
451.779774682

ตรวจสอบว่าอยู่ใต้เส้นโค้งหรือไม่

เขียนฟังก์ชัน under(x,y) เพื่อตรวจสอบว่า จุด (x,y) อยู่ใต้เส้นของฟังก์ชัน f(x) ที่เขียนด้วยฟังก์ชัน func หรือไม่ ให้ฟังก์ชัน under คือค่าเป็น Boolean

ในการเขียนฟังก์ชันดังกล่าวให้เรียกใช้ฟังก์ชัน func ตามที่ได้เขียนไว้จากข้อที่แล้ว แต่ในการตอบไม่ต้องใส่ฟังก์ชันดังกล่าวลงไป

(หมายเหตุถึง TA: ให้เว้นช่องให้เขียนฟังก์ชัน under(x,y) แต่ให้ใส่ฟังก์ชัน func ให้ได้ แต่ซ่อนไว้ ดังด้านล่าง)

def under(x,y):
______________________________________
______________________________________
______________________________________
______________________________________

ตัวอย่างของโปรแกรมหลักที่เรียกใช้ฟังก์ชันดังกล่าว

x = float(input("Enter X: "))
y = float(input("Enter Y: "))
if under(x,y):
    print("It is.")
else:
    print("It is not.")

ตัวอย่างการทำงาน 1

Enter X: 0
Enter Y: 0
It is not.

ตัวอย่างการทำงาน 2

Enter X: 10
Enter Y: 100
It is.

ส่วนคำนวณหลัก

เราจะใช้ฟังก์ชัน random จากโมดูล random ที่คืนค่าระหว่าง 0 ถึง 1 ในการสุ่มตัวเลข อ่านรายละเอียดการใช้ฟังก์ชันดังกล่าวได้จาก http://theory.cpe.ku.ac.th/wiki/index.php/204111:Python_missing_th ส่วนการสุ่มตัวเลข

ในการสุ่มเพื่อประมาณพื้นที่ใต้โค้ง เราจะต้องหาขอบเขตในการสุ่มจุดเสียก่อน ในกรณีนี้เราจะสุ่มจุดที่อยู่ในสี่เหลี่ยมดังรูปด้านล่าง

สังเกตว่าพื้นที่รวมของสี่เหลี่ยมนี้คือ $(b-a)*f(b)$

ให้เขียนฟังก์ชัน area(a,b) ที่รับพารามิเตอร์ a และ b เป็นจำนวนจริง จากนั้นคำนวณค่าประมาณของพื้นที่ใต้เส้นโค้ง $f(x)=x^{2}\cdot (2-2^{-x/100})$ ที่ x มีค่าจาก x = a ถึง x = b โดยใช้การสุ่มจุดจำนวน 10000 จุด ให้ฟังก์ชัน area คืนค่าพื้นที่นั้นออกมา

(หมายเหตุ ให้ใช้ฟังก์ชัน func และ under ที่เขียนจากข้อที่แล้ว)

(คำใบ้: การจะสุ่มค่าระหว่าง a ถึง b สามารถทำได้โดยใช้ฟังก์ชัน random ที่สุ่มค่าจาก 0 ถึง 1 แต่ต้องมีการคำนวณเพิ่มเติมเล็กน้อยหลังจากนั้น เราแนะนำให้เขียนฟังก์ชัน randbetween(a,b) ที่สุ่มค่าจำนวนจริงระหว่าง a ถึง b เพื่อใช้ประกอบ)

ตัวอย่างของโปรแกรมหลักที่เรียกใช้ฟังก์ชันดังกล่าวเป็นดังด้านล่าง

a = float(input("Enter a: "))
b = float(input("Enter b: "))
result = area(a,b)
print("Area = %.3f" % result)

ด้านล่างแสดงตัวอย่างการทำงาน โปรแกรมที่นิสิตเขียนไม่จำเป็นต้องให้ผลลัพธ์ตรงพอดีกับตัวอย่าง แต่ควรมีค่าใกล้เคียง

ตัวอย่างการทำงาน 1

Enter a: 0
Enter b: 10
Area = 353.273

ตัวอย่างการทำงาน 2

Enter a: 100
Enter b: 200
Area = 3820600.000

ให้เขียนฟังก์ชันต่าง ๆ ที่ใช้ทั้งหมด ลงในนี้ ไม่ต้องใส่โปรแกรมหลัก (ถ้าใส่โปรแกรมหลักระบบจะตรวจผิดพลาด)

(หมายเหตุถึง TA: ให้เว้นช่องใหญ่ ๆ สำหรับใส่ฟังก์ชันต่าง ๆ ข้อนี้จะตรวจยากสักหน่อย เดี๋ยวจะมาเขียนอธิบาย)

ทบทวนกลาง

หอยทาก

หอยทากตัวหนึ่ง ตกลงไปในบ่อที่มีความสูง H เมตร มันพยายามจะไต่ให้ถึงปากบ่อ ในเวลากลางวันหอยทากไต่ขึ้นไปได้ U เมตร เวลากลางคืนมันนอนหลับจึงไม่ได้ไต่แต่กลับไถลลงมาเป็นระยะทาง D เมตร ให้เขียนโปรแกรมเพื่อหาว่าหอยทากจะใช้เวลากี่วันในการไต่ออกจากบ่อ

ตัวอย่างการทำงาน 1

H: 5
U: 10
D: 1
1 day(s).

ตัวอย่างการทำงาน 2

H: 5
U: 3
D: 2
3 day(s).