Sgt/eigen1

โค้ดตัวอย่าง

• โค้ดตัวอย่างอยู่ที่ github
• Modules:
  • mat.py: สร้าง adjacency matrix และ degree matrix
  • generators.py: สร้าง adjacency list ของ line และ random graph แบบสอง cluster
  • grpplot.py ส่วนของการ plot
  • main.py: โปรแกรมหลัก

ฟังก์ชัน grpplot.plot

ฟังก์ชัน grpplot.plot(n, adjmat, px, py) จะวาดกราฟ n โหนด ตาม adjacency matrix adjmat โดยใช้พิกัดจาก px และ py

การปรับแก้การแสดงผล:

• สามารถปรับการแสดงโหนดโดยดูจาก เอกสารฟังก์ชัน scatter
• สามารถแก้ไขรูปแบบเส้นโดยดูจาก วิธีการเพิ่มเส้นในการ plot โดยใช้ LineCollection

โปรแกรมหลัก main.py พร้อมคำอธิบาย

def main():
    # สร้าง adjacency list ของกราฟ
    n = 100
    #adjlist = gen_line(n)
    adjlist = gen_random(n,500)

    # สร้าง laplacian ของกราฟ
    a = adjmat(n,adjlist)
    d = degmat(n,adjlist)
    la = d - a

    # คำนวณ eigenvectors, eigenvalues แต่ผลจาก eig ไม่เรียง เลยจับมาเรียงเองด้วย sort_eig
    w,v = eig(la)
    w,v = sort_eig(w,v,n)
    print w

    # eigenvectors ของ $\lambda_2$ และ $\lambda_3$
    e2 = v[1]
    e3 = v[2]

    # แกน x เอามาจาก eigenvectors, แกน y สุ่ม
    px = [e2[i,0] for i in range(n)]
    py = [random() for i in range(n)]

    plot(n,a,px,py)
    raw_input()

การทดลอง Graph drawing

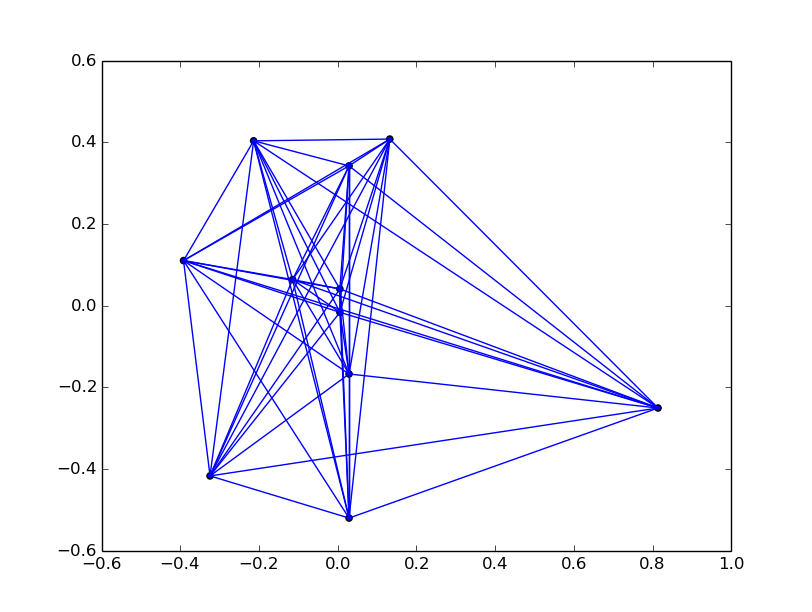
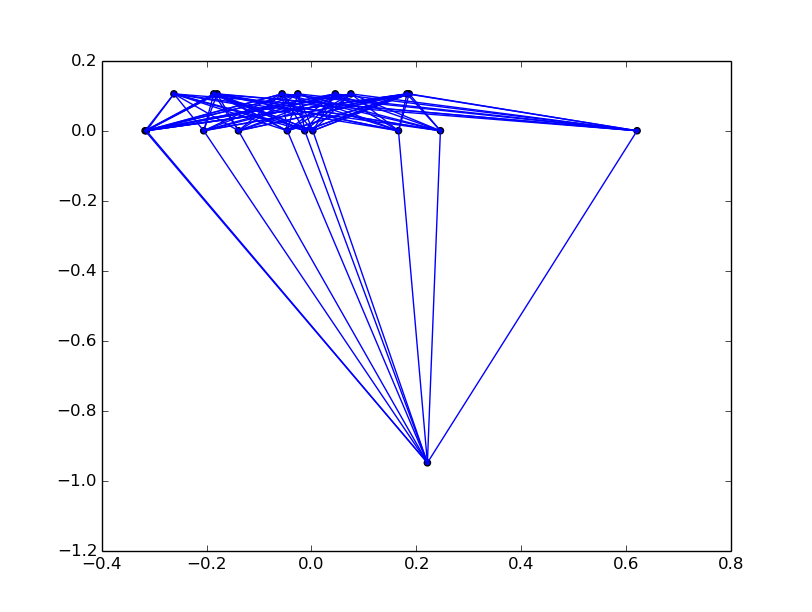
ทดลองใส่กราฟในรูปแบบต่าง ๆ เช่น tree, cycle, complete graphs, grids เป็นต้น แล้ววาดโดยใช้ eigenvector ที่สองและสาม

• 

  Complete graph ขนาด 11 โหนด

• 

  Bipartite graph ขนาด 20 nodes แบ่งเป็น A,B ข้างละ 10 nodes โดยที่ node ใดๆในฝั่ง A เชื่อมไปยังทุก node ในฝั่ง B

การทดลอง Graph Partitioning

Synthetic data

L = D - A = [[10 0 0 0 0 0 0 0 0 0 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1]

[ 0 10  0  0  0  0  0  0  0  0 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1]
[ 0  0 10  0  0  0  0  0  0  0 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1]
[ 0  0  0 10  0  0  0  0  0  0 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1]
[ 0  0  0  0 10  0  0  0  0  0 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1]
[ 0  0  0  0  0 10  0  0  0  0 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1]
[ 0  0  0  0  0  0 10  0  0  0 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1]
[ 0  0  0  0  0  0  0 10  0  0 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1]
[ 0  0  0  0  0  0  0  0 10  0 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1]
[ 0  0  0  0  0  0  0  0  0 10 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1]
[-1 -1 -1 -1 -1 -1 -1 -1 -1 -1 10  0  0  0  0  0  0  0  0  0]
[-1 -1 -1 -1 -1 -1 -1 -1 -1 -1  0 10  0  0  0  0  0  0  0  0]
[-1 -1 -1 -1 -1 -1 -1 -1 -1 -1  0  0 10  0  0  0  0  0  0  0]
[-1 -1 -1 -1 -1 -1 -1 -1 -1 -1  0  0  0 10  0  0  0  0  0  0]
[-1 -1 -1 -1 -1 -1 -1 -1 -1 -1  0  0  0  0 10  0  0  0  0  0]
[-1 -1 -1 -1 -1 -1 -1 -1 -1 -1  0  0  0  0  0 10  0  0  0  0]
[-1 -1 -1 -1 -1 -1 -1 -1 -1 -1  0  0  0  0  0  0 10  0  0  0]
[-1 -1 -1 -1 -1 -1 -1 -1 -1 -1  0  0  0  0  0  0  0 10  0  0]
[-1 -1 -1 -1 -1 -1 -1 -1 -1 -1  0  0  0  0  0  0  0  0 10  0]
[-1 -1 -1 -1 -1 -1 -1 -1 -1 -1  0  0  0  0  0  0  0  0  0 10]]